كيفية إجراء الانحدار الخطي البسيط في spss

الانحدار الخطي البسيط هو طريقة يمكننا استخدامها لفهم العلاقة بين متغير التوقع ومتغير الاستجابة.

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار الخطي البسيط في برنامج SPSS.

مثال: الانحدار الخطي البسيط في برنامج SPSS

لنفترض أن لدينا مجموعة البيانات التالية التي توضح عدد الساعات المدروسة ودرجة الامتحان التي حصل عليها 20 طالبًا:

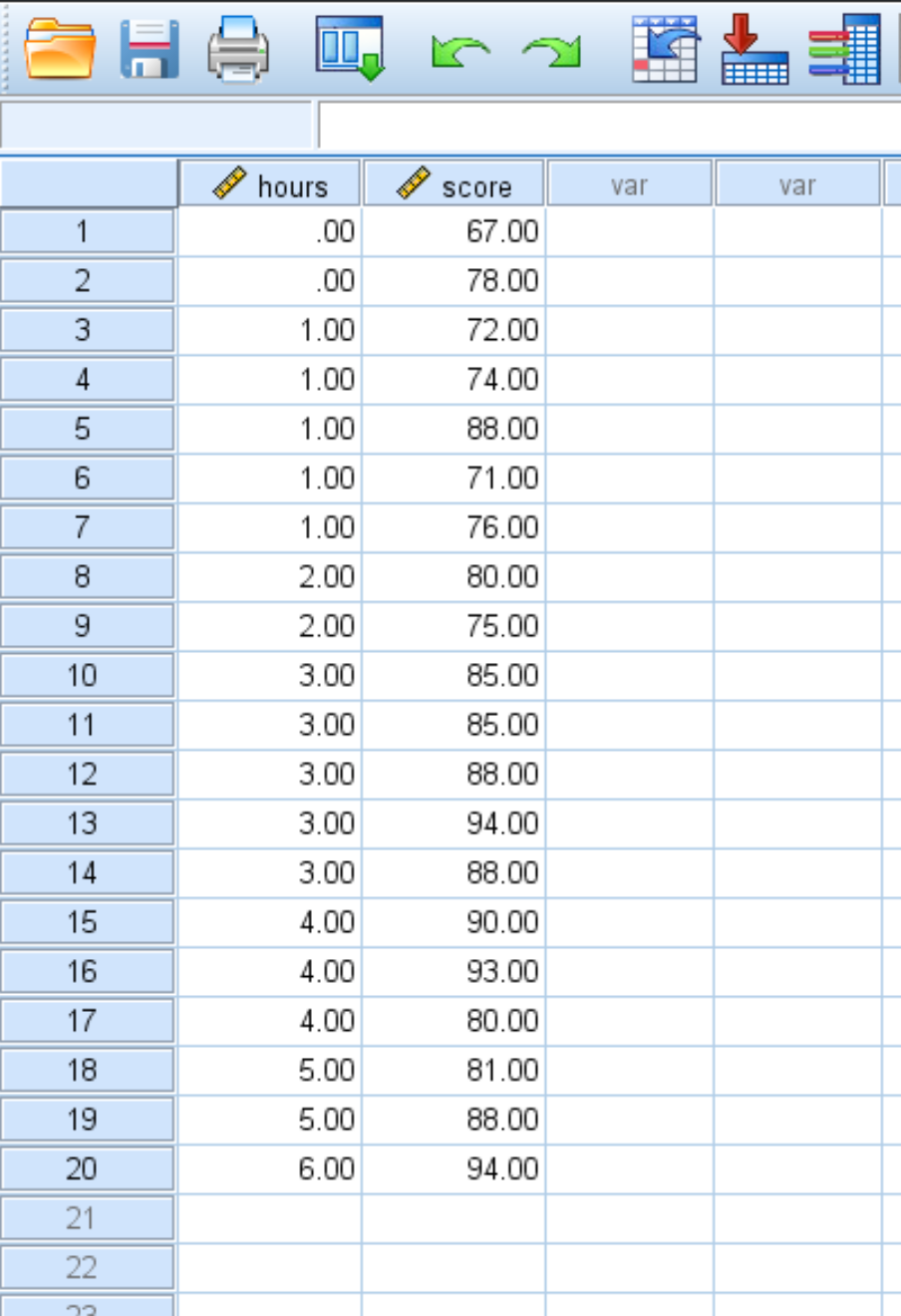
استخدم الخطوات التالية لإجراء انحدار خطي بسيط على مجموعة البيانات هذه لتحديد العلاقة بين ساعات الدراسة ودرجة الاختبار:

الخطوة 1: تصور البيانات.

أولاً، سنقوم بإنشاء مخطط مبعثر لتصور العلاقة بين الساعات والنتيجة للتأكد من أن العلاقة بين المتغيرين تبدو خطية. وبخلاف ذلك، لن يكون الانحدار الخطي البسيط أسلوبًا مناسبًا للاستخدام.

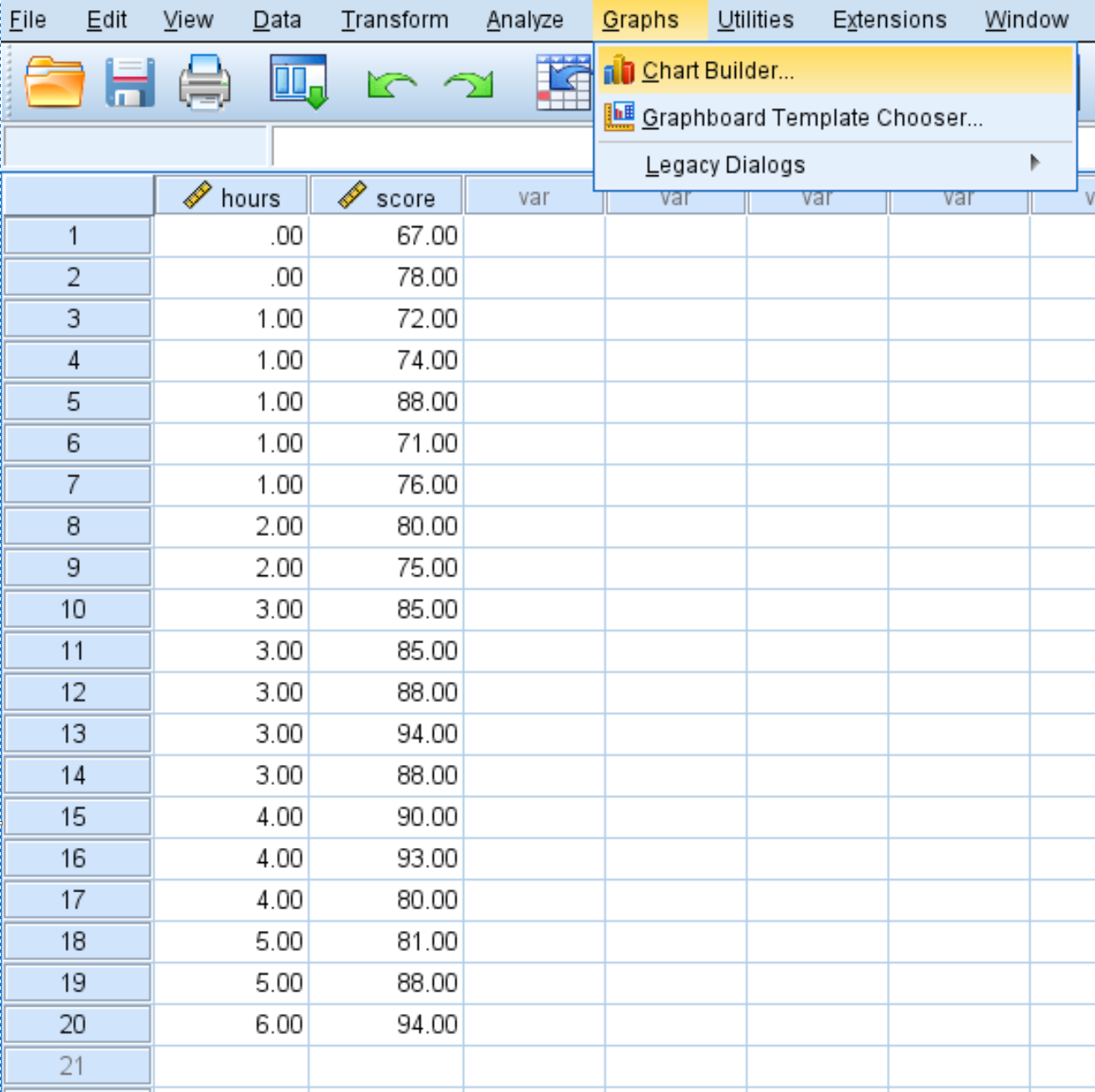
انقر فوق علامة التبويب “المخططات” ، ثم انقر فوق “منشئ المخططات” :

من قائمة “اختيار من” ، انقر واسحب Scatter/Dot إلى نافذة التحرير الرئيسية. ثم اسحب الأوقات المتغيرة إلى المحور السيني والنتيجة على المحور الصادي.

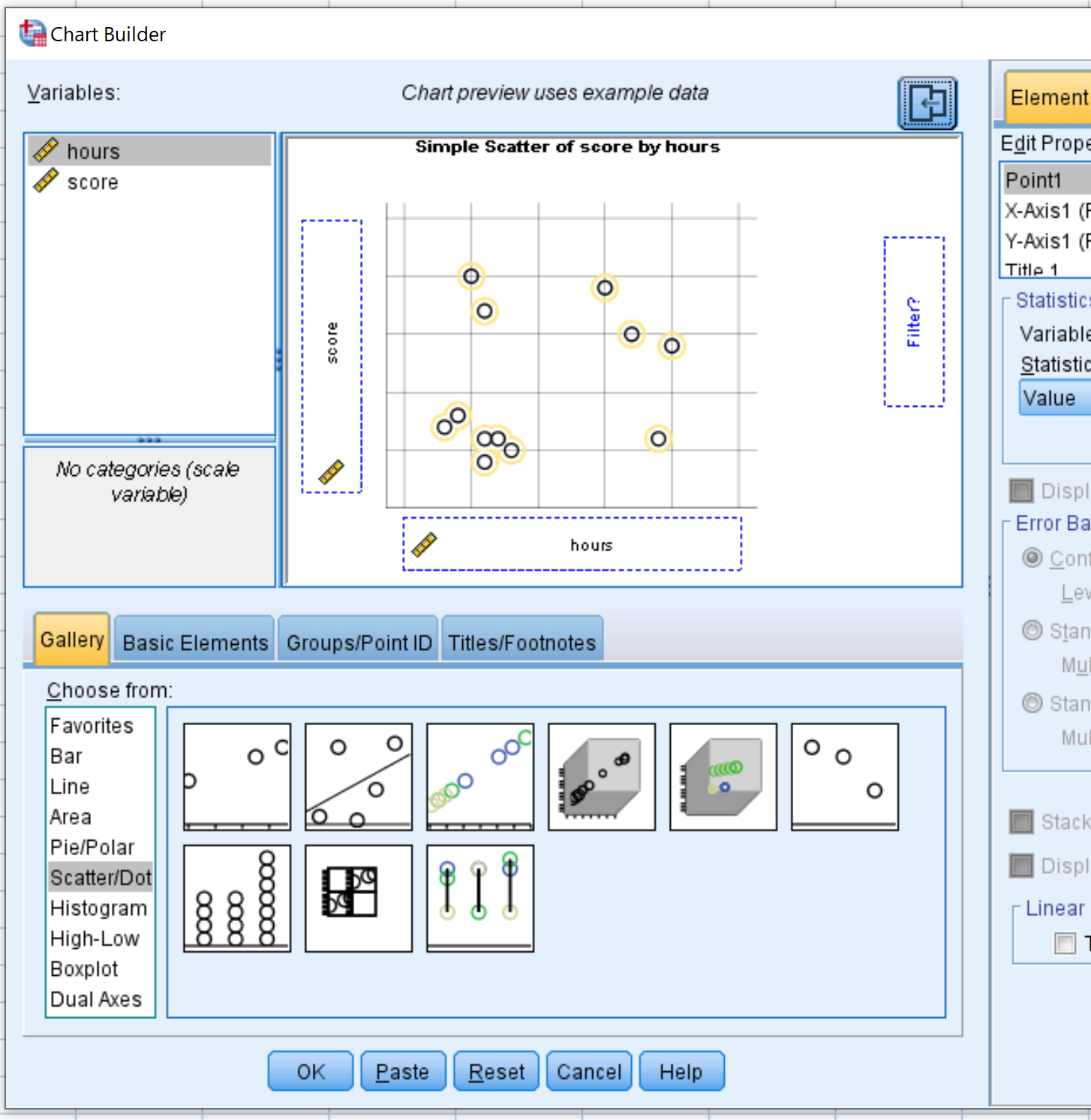
بمجرد النقر فوق “موافق” ، سيظهر المخطط المبعثر التالي:

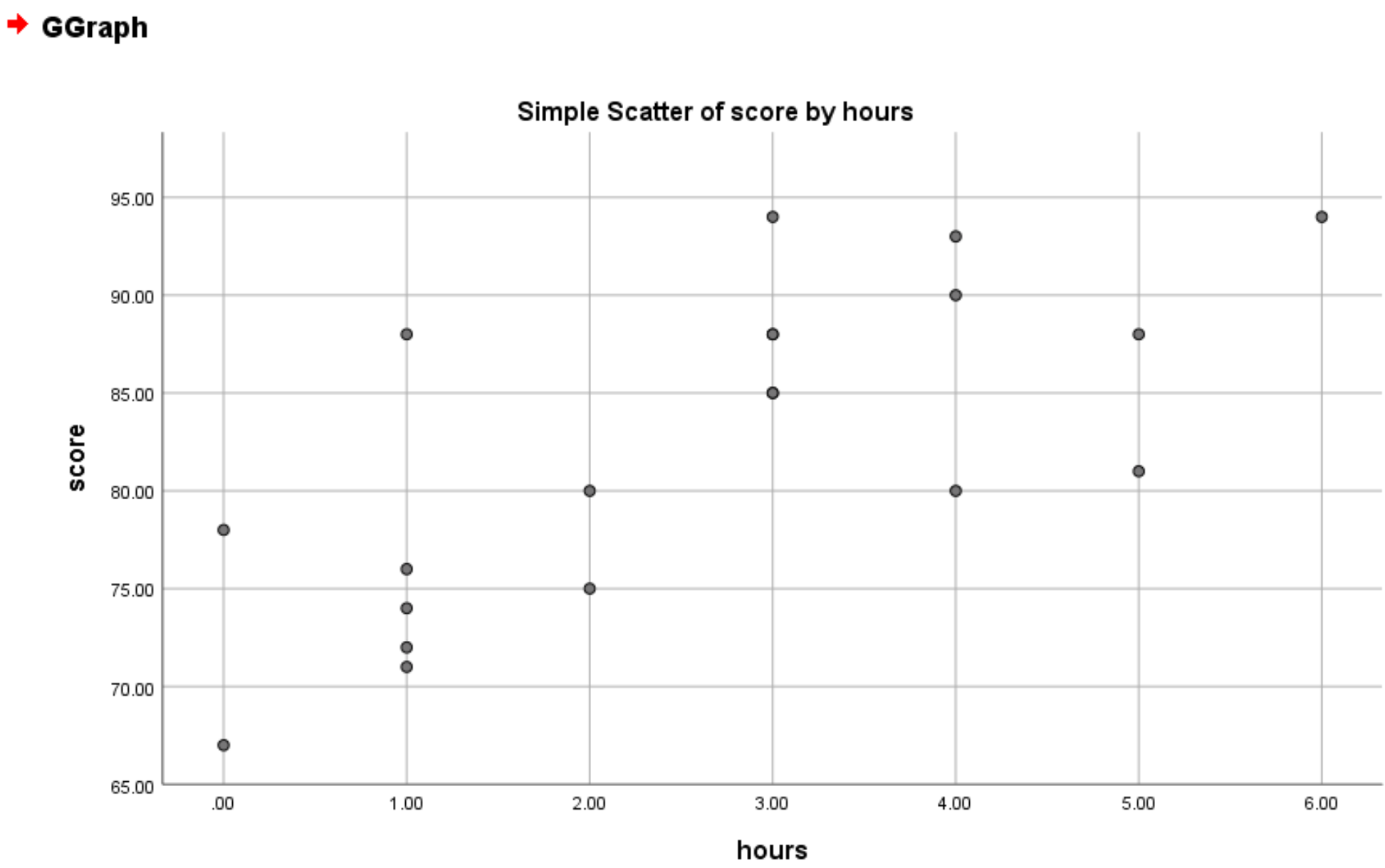
من الرسم البياني، يمكننا أن نرى أن هناك علاقة خطية موجبة بين الساعات والنتيجة. بشكل عام، الطلاب الذين يدرسون ساعات أكثر يميلون إلى الحصول على درجات أعلى.

وبما أن هناك علاقة خطية واضحة بين المتغيرين، فسوف ننتقل إلى ملاءمة نموذج الانحدار الخطي البسيط لمجموعة البيانات.

الخطوة 2: تناسب نموذج الانحدار الخطي البسيط.

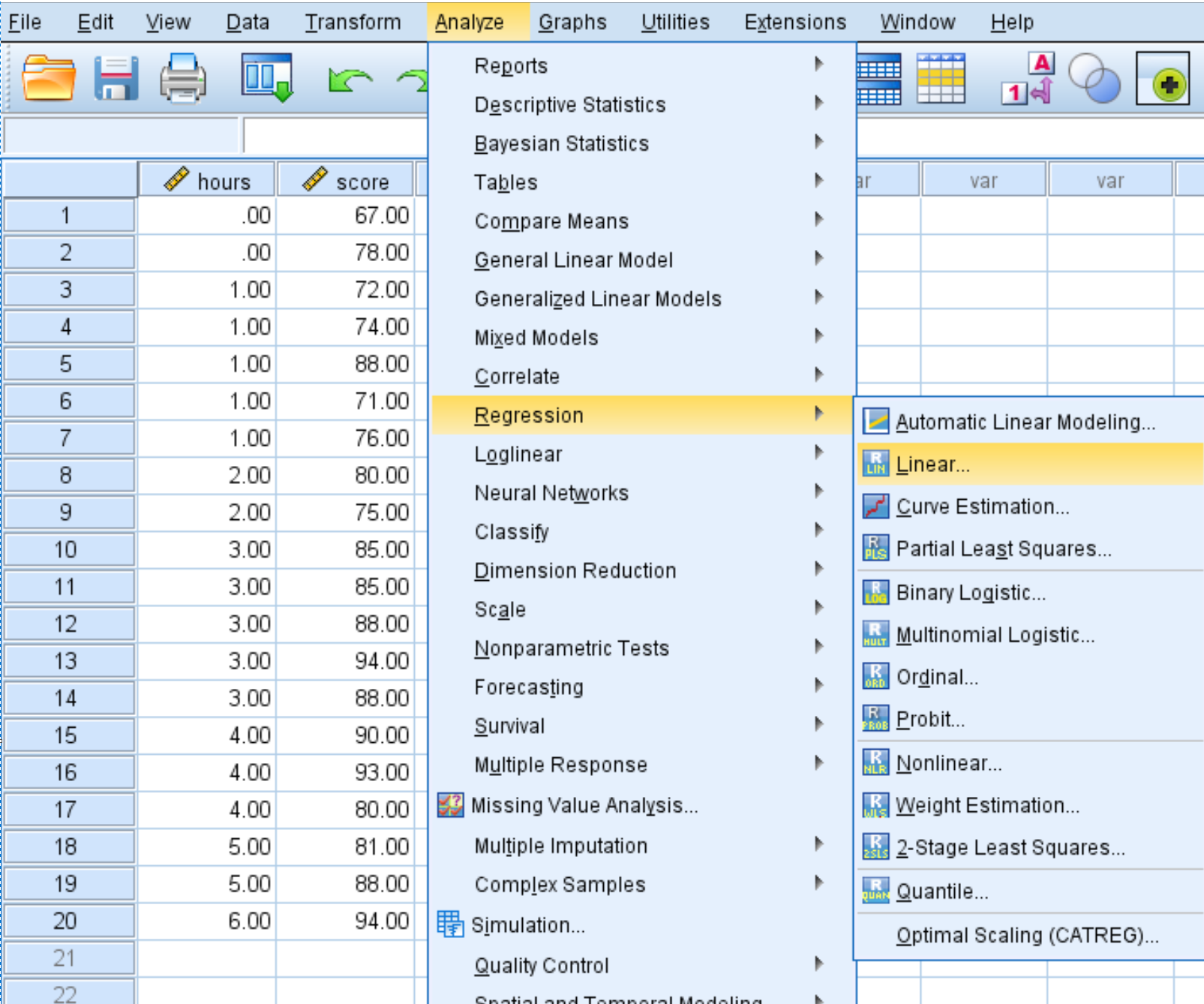
انقر فوق علامة التبويب تحليل ، ثم الانحدار ، ثم الخطي :

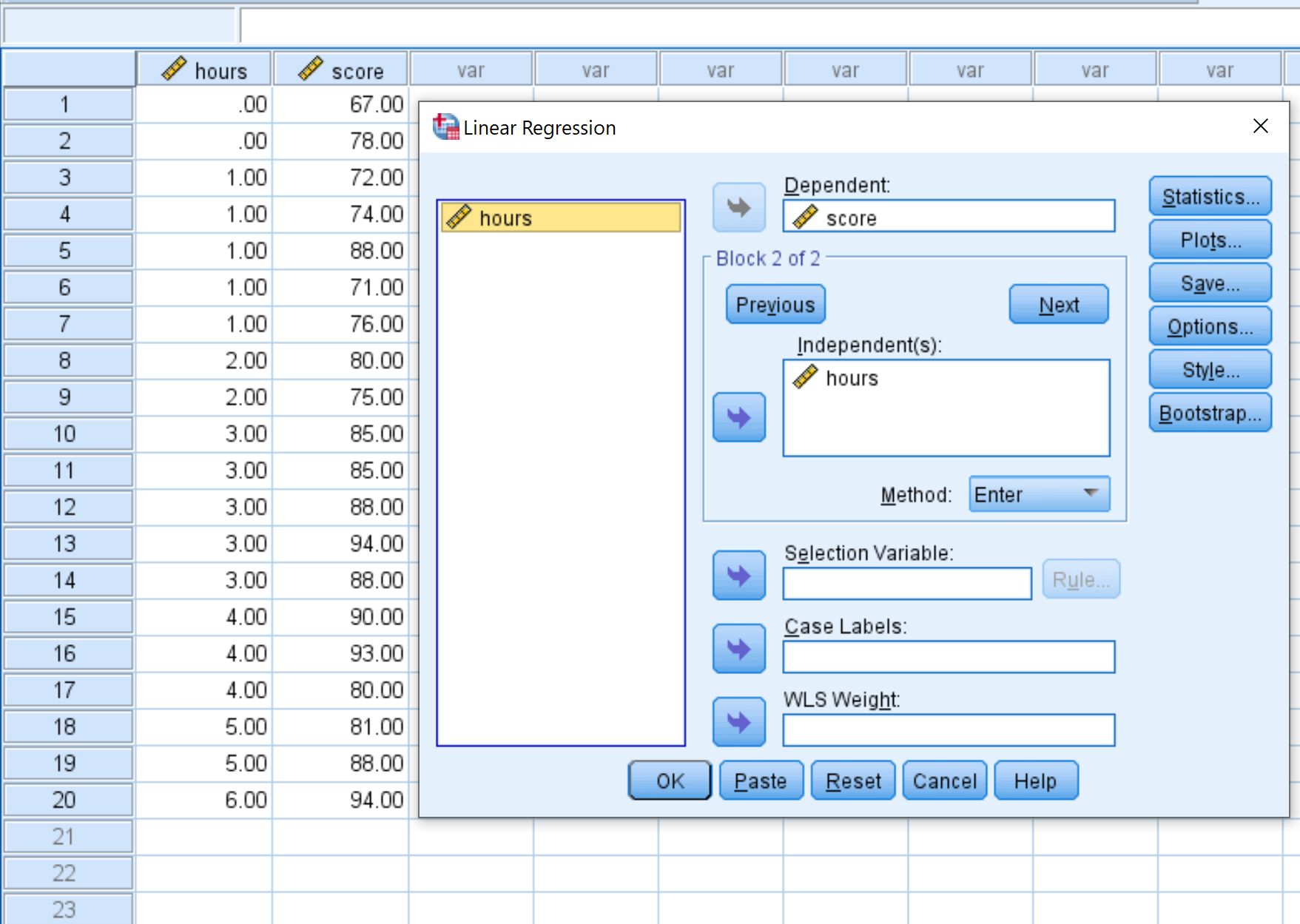
في النافذة الجديدة التي تظهر، اسحب درجة المتغير إلى المربع المسمى “تابع” واسحب الساعات إلى المربع المسمى “مستقل”. ثم انقر فوق موافق .

الخطوة 3: تفسير النتائج.

بمجرد النقر فوق “موافق” ، ستظهر نتائج الانحدار الخطي البسيط. الجدول الأول الذي يهمنا هو الجدول الذي يحمل عنوان ملخص النموذج :

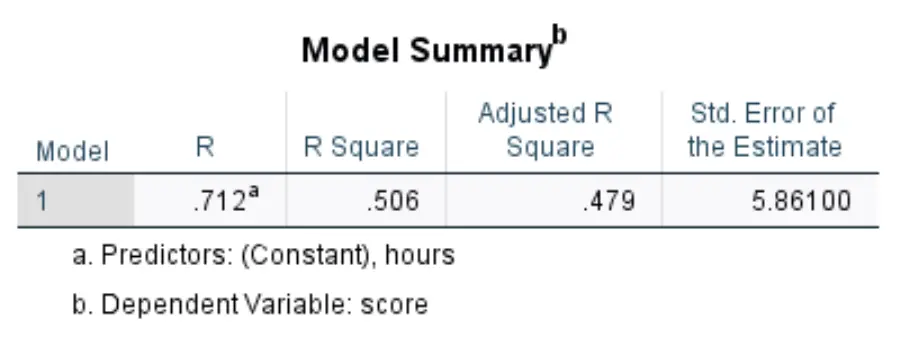
فيما يلي كيفية تفسير الأرقام الأكثر صلة في هذا الجدول:

• مربع R: هو نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بالمتغير التوضيحي. في هذا المثال، يمكن تفسير 50.6% من التباين في درجات الامتحان من خلال ساعات الدراسة.
• معيار. خطأ التقدير: الخطأ القياسي هو متوسط المسافة بين القيم المرصودة وخط الانحدار. في هذا المثال، تنحرف القيم المرصودة في المتوسط بمقدار 5861 وحدة عن خط الانحدار.

الجدول التالي الذي يهمنا هو بعنوان المعاملات :

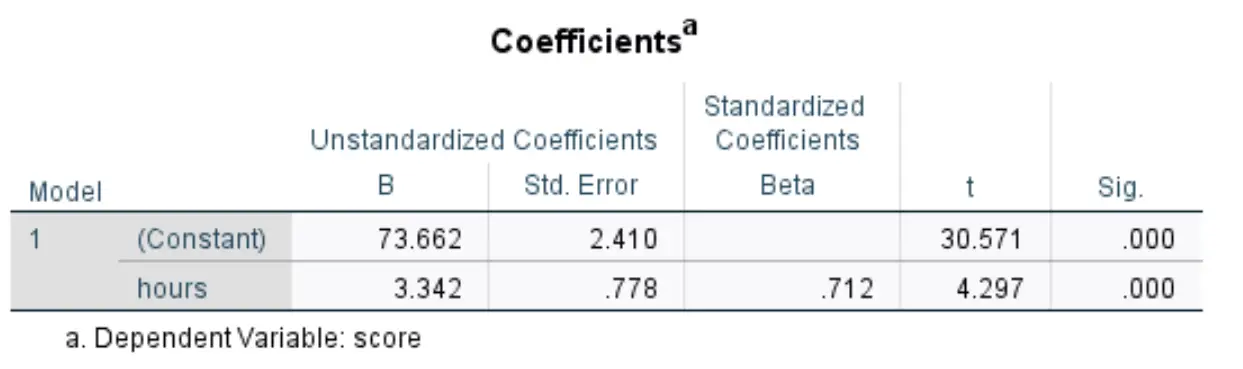
فيما يلي كيفية تفسير الأرقام الأكثر صلة في هذا الجدول:

• غير قياسي B (ثابت) : يخبرنا هذا بالقيمة المتوسطة لمتغير الاستجابة عندما يكون المتغير المتنبئ صفراً. في هذا المثال، متوسط درجات الامتحان هو 73.662 عندما تكون الساعات المدروسة صفرًا.
• ب غير قياسي (ساعات): يخبرنا بمتوسط التغير في متغير الاستجابة المرتبط بزيادة وحدة واحدة في المتغير المتنبئ. في هذا المثال، ترتبط كل ساعة إضافية تتم دراستها بزيادة قدرها 3342 في درجة الاختبار في المتوسط.
• Sig (ساعات): هذه هي القيمة p المرتبطة بإحصائيات الاختبار خلال الساعات. في هذه الحالة، وبما أن هذه القيمة أقل من 0.05، يمكننا أن نستنتج أن متغير الساعات المتنبئ له دلالة إحصائية.

وأخيرا يمكننا تكوين معادلة انحدار باستخدام قيم الثابت والساعات . وفي هذه الحالة ستكون المعادلة:

درجة الامتحان المقدرة = 73.662 + 3.342*(ساعات)

يمكننا استخدام هذه المعادلة للعثور على درجة الامتحان المقدرة للطالب، بناءً على عدد الساعات المدروسة.

على سبيل المثال، الطالب الذي يدرس لمدة 3 ساعات يجب أن يحقق درجة الامتحان 83.688:

درجة الاختبار المقدرة = 73.662 + 3.342*(3) = 83.688

الخطوة 4: الإبلاغ عن النتائج.

وأخيرًا، نريد تلخيص نتائج الانحدار الخطي البسيط. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء الانحدار الخطي البسيط لتحديد العلاقة بين ساعات الدراسة ودرجة الامتحان. تم استخدام عينة مكونة من 20 طالبا في التحليل.

وأظهرت النتائج أن هناك علاقة ذات دلالة إحصائية بين ساعات الدراسة ودرجة الامتحان (t = 4.297، p <0.000) وأن ساعات الدراسة شكلت 50.6٪ من التباين الموضح في درجة الامتحان. الامتحان.

وتبين أن معادلة الانحدار هي:

درجة الامتحان المقدرة = 73.662 + 3.342*(ساعات)

وترتبط كل ساعة إضافية تتم دراستها بزيادة قدرها 3342 في درجة الامتحان في المتوسط.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في SPSS:

كيفية إجراء الانحدار الخطي المتعدد في SPSS
كيفية إجراء الانحدار التربيعي في SPSS
كيفية إجراء الانحدار اللوجستي في SPSS