كيفية إجراء الانحدار الكمي في r

الانحدار الخطي هو أسلوب يمكننا استخدامه لفهم العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .

عادةً، عندما نقوم بإجراء الانحدار الخطي، نريد تقدير متوسط قيمة متغير الاستجابة.

ومع ذلك، يمكننا بدلاً من ذلك استخدام طريقة تُعرف باسم الانحدار الكمي لتقدير أي قيمة كمية أو مئوية لقيمة الاستجابة، مثل المئين السبعين، والمئين التسعين، والمئين 98، وما إلى ذلك.

لإجراء الانحدار الكمي في R، يمكننا استخدام الدالة rq() من الحزمة quantreg ، والتي تستخدم بناء الجملة التالي:

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

ذهب:

• y: متغير الاستجابة
• x: المتغير (المتغيرات) التنبؤية
• البيانات: اسم مجموعة البيانات
• تاو: النسبة المئوية للعثور عليها. الافتراضي هو الوسيط (tau = 0.5)، ولكن يمكنك تعيينه على أي رقم بين 0 و1.

يوفر هذا البرنامج التعليمي مثالاً خطوة بخطوة حول كيفية استخدام هذه الوظيفة لإجراء الانحدار الكمي في R.

الخطوة 1: أدخل البيانات

في هذا المثال، سنقوم بإنشاء مجموعة بيانات تحتوي على الساعات التي تمت دراستها ونتائج الامتحانات التي تم الحصول عليها لـ 100 طالب مختلف في إحدى الجامعات:

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

الخطوة 2: تنفيذ الانحدار الكمي

بعد ذلك، سنلائم نموذج الانحدار الكمي باستخدام ساعات الدراسة كمتغير متوقع ودرجات الامتحان كمتغير الاستجابة.

سوف نستخدم النموذج للتنبؤ بنسبة التسعين المئوية المتوقعة من درجات الامتحان بناءً على عدد ساعات الدراسة:

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

من النتيجة يمكننا أن نرى معادلة الانحدار المقدرة:

درجة الامتحان المئوي التسعون = 60.25 + 2.437*(ساعات)

على سبيل المثال، يجب أن تكون النتيجة المئوية التسعين لجميع الطلاب الذين يدرسون 8 ساعات 79.75:

المئين التسعون من درجة الامتحان = 60.25 + 2.437*(8) = 79.75 .

يعرض الإخراج أيضًا حدود الثقة العلوية والسفلية للتقاطع وأوقات متغير التوقع.

الخطوة 3: تصور النتائج

يمكننا أيضًا تصور نتائج الانحدار عن طريق إنشاء مخطط مبعثر مع معادلة الانحدار الكمي المجهزة المتراكبة على الرسم البياني:

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

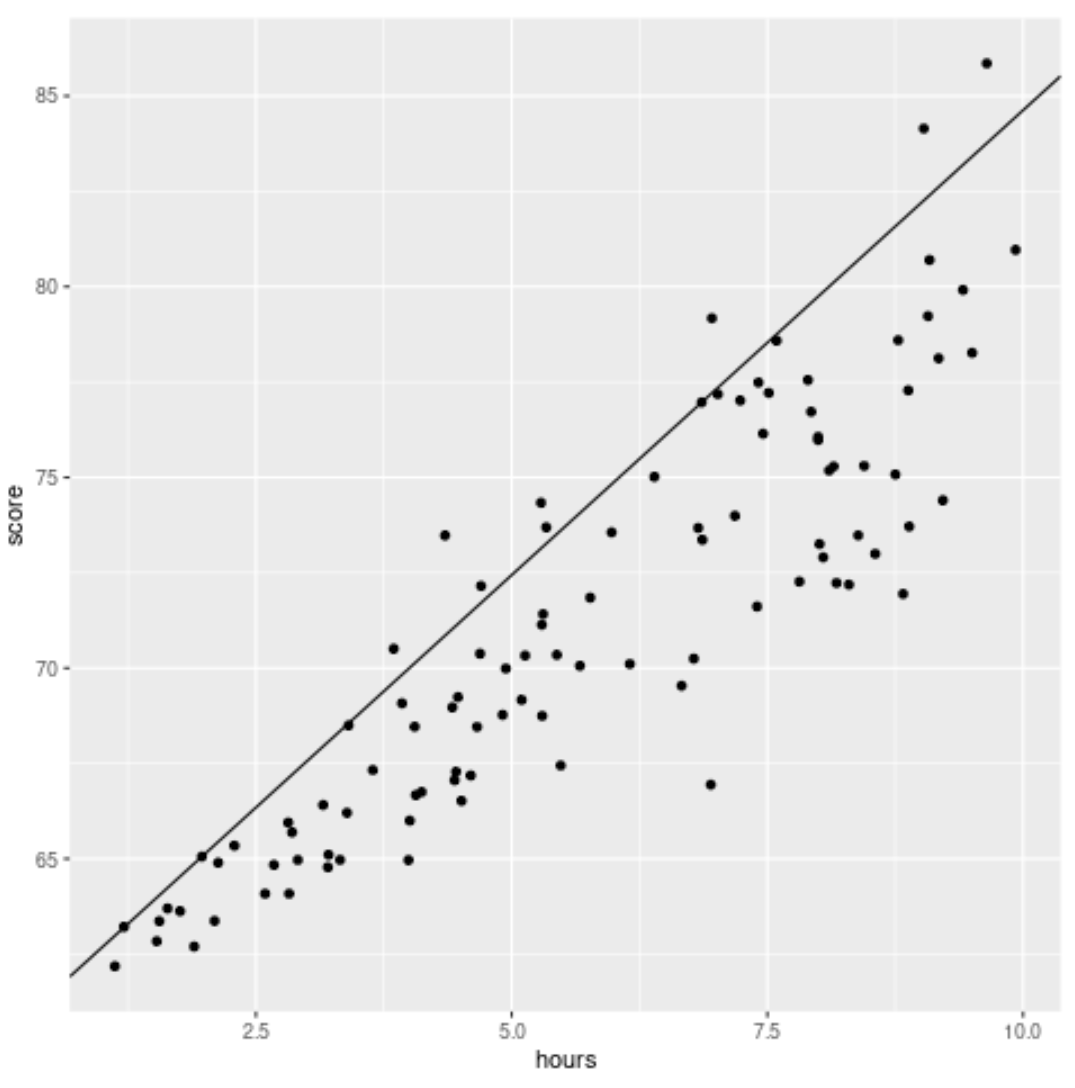
على عكس خط الانحدار الخطي التقليدي، لاحظ أن هذا الخط المجهز لا يمر عبر قلب البيانات. وبدلاً من ذلك، فإنه يمر عبر النسبة المئوية التسعين المقدرة في كل مستوى من متغير التوقع.

يمكننا أن نرى الفرق بين معادلة الانحدار الكمي المجهزة ومعادلة الانحدار الخطي البسيطة عن طريق إضافة الوسيطة Geom_smooth() :

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

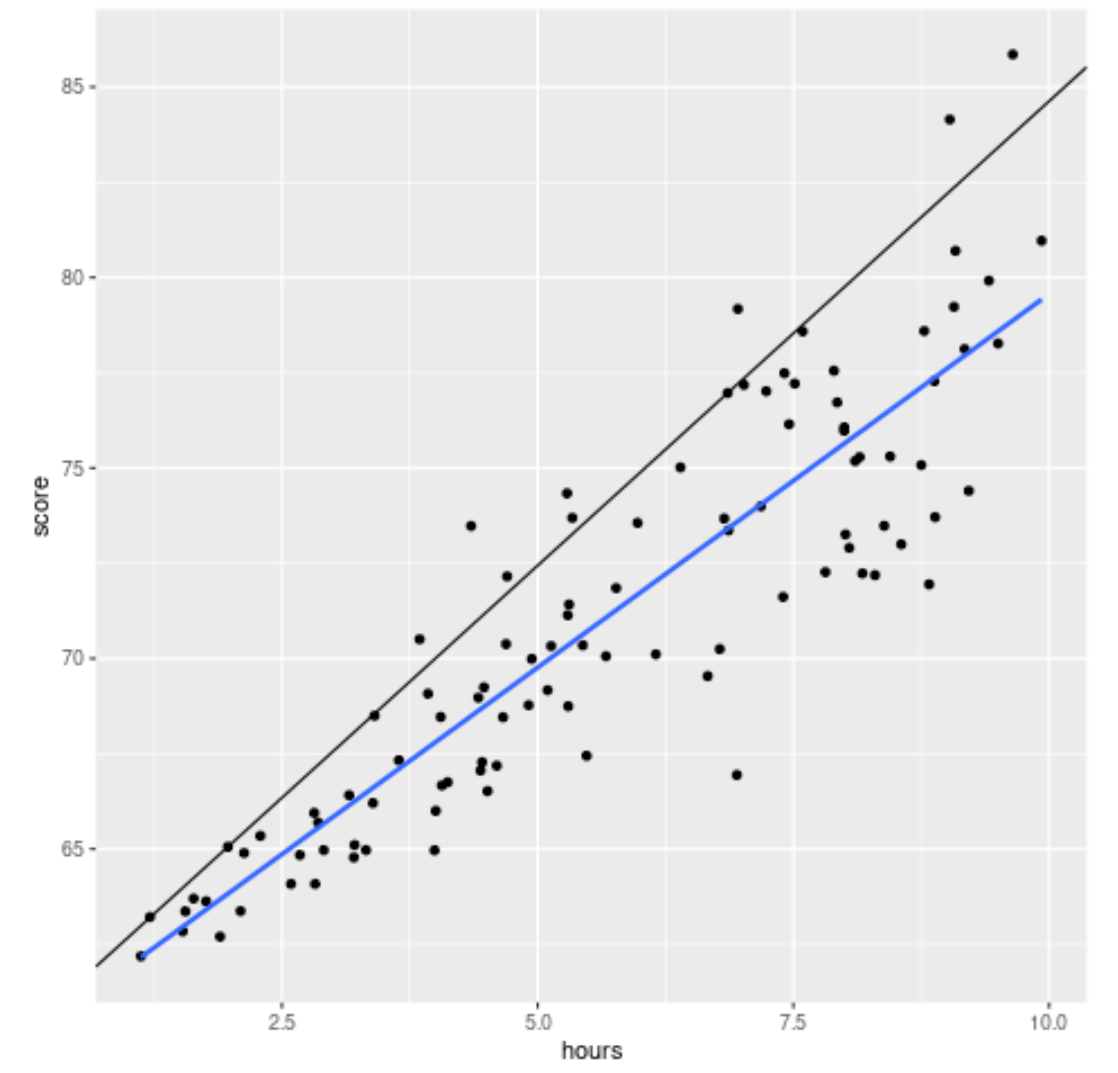
يعرض الخط الأسود خط الانحدار الكمي المعدل للشريحة المئوية التسعين ويعرض الخط الأزرق خط الانحدار الخطي البسيط، الذي يقدر القيمة المتوسطة لمتغير الاستجابة.

كما هو متوقع، يمر خط الانحدار الخطي البسيط عبر البيانات ويوضح لنا القيمة المتوسطة المقدرة لدرجات الاختبار في كل مستوى ساعة.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في R:

كيفية إجراء الانحدار الخطي البسيط في R
كيفية إجراء الانحدار الخطي المتعدد في R
كيفية إجراء الانحدار التربيعي في R