الانحدار اللوجستي مقابل الانحدار الخطي: الاختلافات الرئيسية

اثنان من نماذج الانحدار الأكثر استخدامًا هما الانحدار الخطي والانحدار اللوجستي .

يتم استخدام كلا النوعين من نماذج الانحدار لتحديد العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة ، ولكن هناك بعض الاختلافات الرئيسية بين النموذجين:

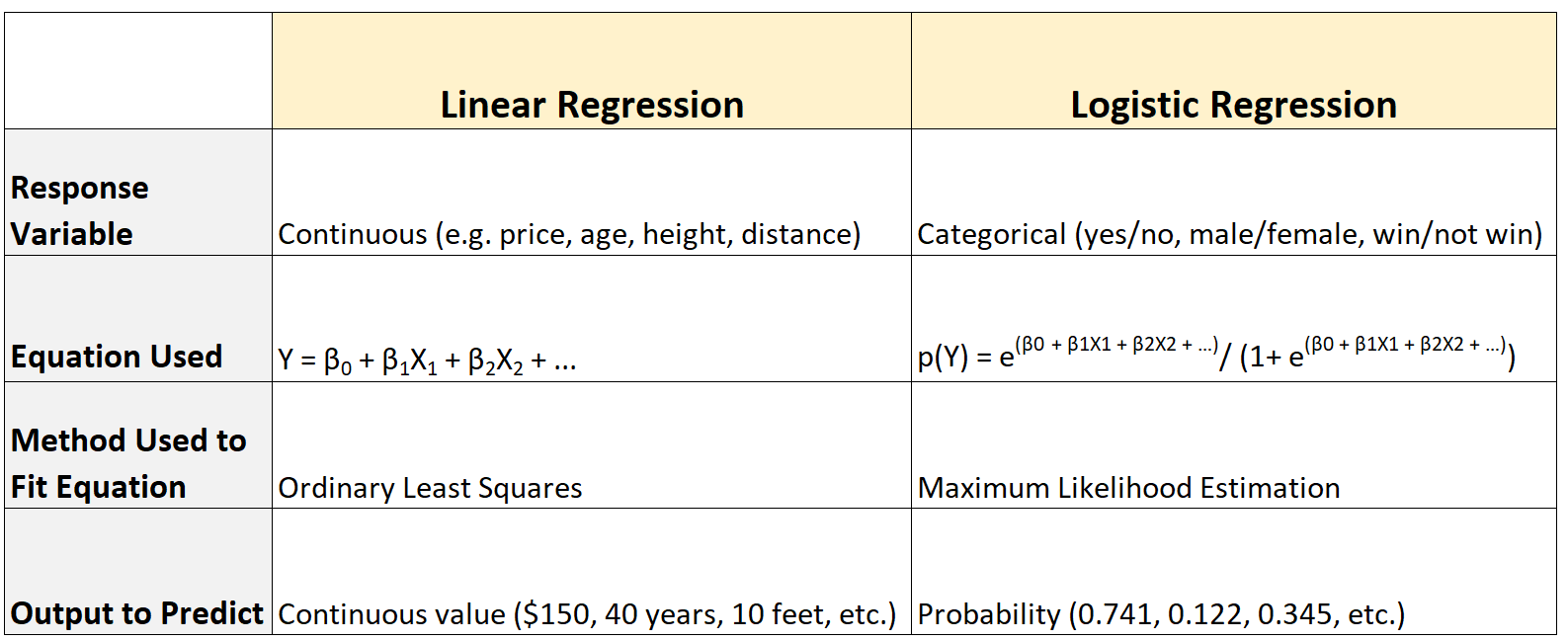
وفيما يلي ملخص للاختلافات:

الفرق رقم 1: نوع متغير الاستجابة

يتم استخدام نموذج الانحدار الخطي عندما يأخذ متغير الاستجابة قيمة مستمرة مثل:

• سعر
• ارتفاع
• عمر
• مسافة

وعلى العكس من ذلك، يتم استخدام نموذج الانحدار اللوجستي عندما يأخذ متغير الاستجابة قيمة فئوية مثل:

• نعم أو لا
• ذكر أم أنثى
• الفوز أو عدم الفوز

الفرق رقم 2: المعادلة المستخدمة

يستخدم الانحدار الخطي المعادلة التالية لتلخيص العلاقة بين متغير (متغيرات) التوقع ومتغير الاستجابة:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

ذهب:

• Y: متغير الاستجابة
• X _j : ^{المتغير} التنبئي j
• β _j : متوسط التأثير على Y لزيادة وحدة واحدة في X _j ، مع تثبيت جميع المتنبئات الأخرى

وعلى العكس من ذلك، يستخدم الانحدار اللوجستي المعادلة التالية:

ص(X) = ه ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} ص

تُستخدم هذه المعادلة للتنبؤ باحتمالية وقوع ملاحظة فردية ضمن فئة معينة.

الفرق رقم 3: الطريقة المستخدمة لملاءمة المعادلة

يستخدم الانحدار الخطي طريقة تعرف باسم المربعات الصغرى العادية للعثور على معادلة الانحدار الأكثر ملائمة.

على العكس من ذلك، يستخدم الانحدار اللوجستي طريقة تعرف باسم تقدير الاحتمالية القصوى للعثور على معادلة الانحدار الأكثر ملائمة.

الفرق رقم 4: الإخراج المتوقع

يتنبأ الانحدار الخطي بقيمة مستمرة كمخرجات. على سبيل المثال:

• السعر (150 دولارًا، 199 دولارًا، 400 دولارًا، وما إلى ذلك)
• الارتفاع (14 بوصة، 2 قدم، 94.32 سم، إلخ.)
• العمر (شهرين، 6 سنوات، 41.5 سنة، إلخ.)
• المسافة (1.23 ميل، 4.5 كيلومتر، إلخ)

وعلى العكس من ذلك، يتنبأ الانحدار اللوجستي بالاحتمالات كنتيجة. على سبيل المثال:

• 40.3% فرصة للقبول في إحدى الجامعات.
• فرصة الفوز باللعبة 93.2%.
• 34.2% فرصة لإقرار القانون.

متى يتم استخدام الانحدار اللوجستي أو الخطي

يمكن أن تساعدك المشكلات التدريبية التالية على فهم أفضل للوقت الذي يجب فيه استخدام الانحدار اللوجستي أو الانحدار الخطي.

المشكلة رقم 1: الدخل السنوي

لنفترض أن أحد الاقتصاديين يريد استخدام المتغيرات المتوقعة (1) ساعات العمل الأسبوعية و(2) سنوات التعليم للتنبؤ بالدخل السنوي للأفراد.

في هذا السيناريو، سيستخدم الانحدار الخطي لأن متغير الاستجابة (الدخل السنوي) مستمر.

المشكلة رقم 2: القبول في الكلية

لنفترض أن مسؤول القبول في الكلية يريد استخدام متغيرات التوقع (1) المعدل التراكمي (GPA) و(2) درجة ACT للتنبؤ باحتمالية قبول الطالب في جامعة معينة.

في هذا السيناريو، ستستخدم الانحدار اللوجستي لأن متغير الاستجابة قاطع ويمكن أن يأخذ قيمتين فقط: مقبول أو غير مقبول.

المشكلة رقم 3: أسعار العقارات

لنفترض أن وكيل عقاري يريد استخدام المتغيرات المتوقعة (1) بالقدم المربع، (2) عدد غرف النوم، و(3) عدد الحمامات للتنبؤ بأسعار مبيعات المنازل.

في هذا السيناريو، ستستخدم الانحدار الخطي لأن متغير الاستجابة (السعر) مستمر.

المشكلة رقم 4: اكتشاف البريد العشوائي

لنفترض أن مبرمج كمبيوتر يريد استخدام متغيرات التوقع (1) عدد الكلمات و(2) بلد المنشأ للتنبؤ باحتمال أن تكون رسالة بريد إلكتروني معينة بريدًا عشوائيًا.

في هذا السيناريو، سيتم استخدام الانحدار اللوجستي لأن متغير الاستجابة قاطع ويمكن أن يأخذ قيمتين فقط: بريد عشوائي أو ليس بريد عشوائي.

مصادر إضافية

تقدم البرامج التعليمية التالية مزيدًا من التفاصيل حول الانحدار الخطي:

• مقدمة إلى الانحدار الخطي البسيط
• مقدمة في الانحدار الخطي المتعدد
• 4 أمثلة لاستخدام الانحدار الخطي في الحياة الحقيقية

تقدم البرامج التعليمية التالية مزيدًا من التفاصيل حول الانحدار اللوجستي:

• مقدمة في الانحدار اللوجستي
• 4 أمثلة لاستخدام الانحدار اللوجستي في الحياة الحقيقية