الانحدار متعدد الحدود في r (خطوة بخطوة)

الانحدار متعدد الحدود هو أسلوب يمكننا استخدامه عندما تكون العلاقة بين متغير التوقع ومتغير الاستجابة غير خطية.

هذا النوع من الانحدار يأخذ الشكل:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

حيث h هي “درجة” كثيرة الحدود.

يوفر هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية تنفيذ الانحدار متعدد الحدود في R.

الخطوة 1: إنشاء البيانات

في هذا المثال، سنقوم بإنشاء مجموعة بيانات تحتوي على عدد ساعات الدراسة ودرجة الاختبار النهائي لفئة مكونة من 50 طالبًا:

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

الخطوة 2: تصور البيانات

قبل ملاءمة نموذج الانحدار للبيانات، دعونا أولاً ننشئ مخططًا مبعثرًا لتصور العلاقة بين ساعات الدراسة ودرجة الامتحان:

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

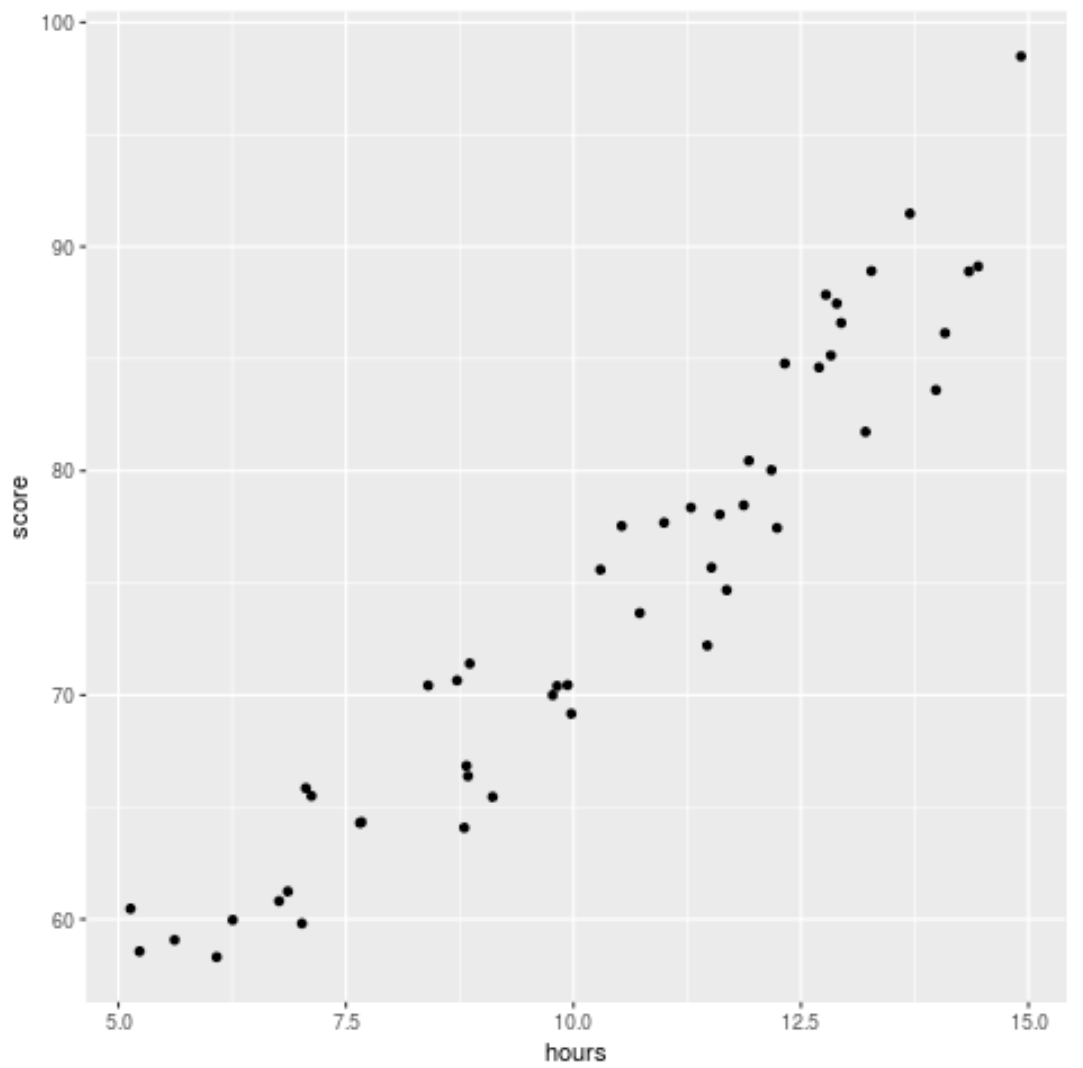
يمكننا أن نرى أن البيانات لها علاقة تربيعية قليلاً، مما يشير إلى أن الانحدار متعدد الحدود قد يناسب البيانات بشكل أفضل من الانحدار الخطي البسيط.

الخطوة 3: تناسب نماذج الانحدار متعدد الحدود

بعد ذلك، سنلائم خمسة نماذج انحدار متعددة الحدود مختلفة بالدرجات h = 1…5 ونستخدم التحقق المتقاطع k-fold مع k = 10 مرات لحساب اختبار MSE لكل نموذج:

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

ومن النتيجة يمكننا أن نرى اختبار MSE لكل نموذج:

• اختبار MSE بدرجة h = 1: 9.80
• اختبار MSE بدرجة ح = 2: 8.75
• اختبار MSE بدرجة ح = 3: 9.60
• اختبار MSE بدرجة h = 4: 10.59
• اختبار MSE بدرجة h = 5: 13.55

تبين أن النموذج ذو أدنى اختبار MSE هو نموذج الانحدار متعدد الحدود بدرجة h = 2.

يتطابق هذا مع حدسنا من مخطط التشتت الأصلي: نموذج الانحدار التربيعي يناسب البيانات بشكل أفضل.

الخطوة 4: تحليل النموذج النهائي

وأخيرا يمكننا الحصول على معاملات النموذج الأفضل أداء:

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ومن النتيجة نرى أن النموذج النهائي المجهز هو:

النتيجة = 54.00526 – 0.07904*(ساعات) + 0.18596*(ساعات) ²

يمكننا استخدام هذه المعادلة لتقدير الدرجة التي سيحصل عليها الطالب بناءً على عدد الساعات التي يدرسها.

على سبيل المثال الطالب الذي يدرس 10 ساعات يجب أن يحصل على درجة 71.81 :

النتيجة = 54.00526 – 0.07904*(10) + 0.18596*(10) ² = 71.81

يمكننا أيضًا رسم النموذج المجهز لمعرفة مدى ملاءمته للبيانات الأولية:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

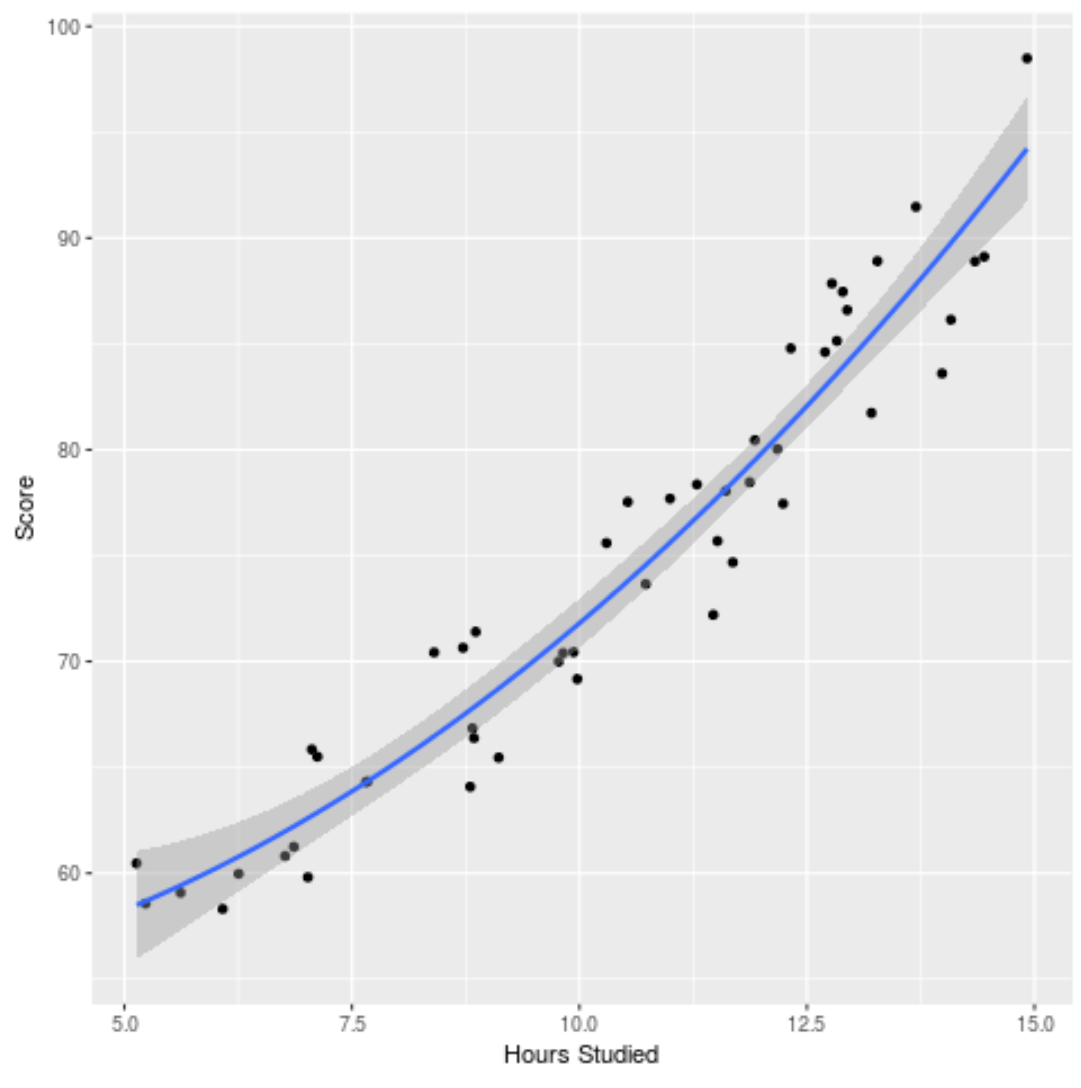
يمكنك العثور على رمز R الكامل المستخدم في هذا المثال هنا .