الانحدار متعدد الحدود

By دكتور بنيامين أندرسون زومار 2, 2023 إحصائيات 0 Comments

تشرح هذه المقالة ما هو الانحدار متعدد الحدود في الإحصائيات وكيفية تنفيذه. بالإضافة إلى ذلك، سوف تكون قادرًا على رؤية مثال يتم فيه تنفيذ الانحدار متعدد الحدود.

ما هو الانحدار متعدد الحدود؟

الانحدار متعدد الحدود ، أو الانحدار متعدد الحدود ، هو نموذج انحدار يتم فيه نمذجة العلاقة بين المتغير المستقل X والمتغير التابع Y باستخدام متعدد الحدود.

على سبيل المثال، معادلة نموذج الانحدار التربيعي متعدد الحدود هي y=β ₀ +β ₁ x+β ₂ x ² +ε.

يعد الانحدار متعدد الحدود مفيدًا لتركيب مجموعات البيانات التي تكون رسومها البيانية عبارة عن منحنيات متعددة الحدود. لذلك، إذا كان المخطط النقطي لعينة البيانات له شكل القطع المكافئ، فسيكون من الأفضل بناء نموذج الانحدار التربيعي بدلاً من نموذج الانحدار الخطي. بهذه الطريقة، ستناسب معادلة نموذج الانحدار عينة البيانات بشكل أفضل.

لاحظ أن الانحدار متعدد الحدود هو نوع من الانحدار غير الخطي، تمامًا مثل الانحدار الأسي والانحدار اللوغاريتمي.

صيغة الانحدار متعدد الحدود

معادلة نموذج الانحدار متعدد الحدود هي y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

ذهب:

$y$

هو المتغير التابع.
$x$

هو المتغير المستقل.
$\beta_0$

هو ثابت معادلة الانحدار متعدد الحدود.
$\beta_i$

هو معامل الانحدار المرتبط بالمتغير

$x^i$

.
$\bm{\varepsilon}$

هذا هو الخطأ أو المتبقي، أي الفرق بين القيمة المرصودة والقيمة المقدرة بواسطة النموذج.

لذلك إذا كان لدينا عينة بإجمالي

$n$

الملاحظات، يمكننا اقتراح نموذج الانحدار متعدد الحدود في شكل مصفوفة:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

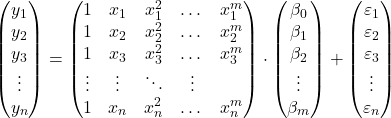
يمكن إعادة كتابة تعبير المصفوفة أعلاه عن طريق تخصيص حرف لكل مصفوفة:

$Y=X\beta+\varepsilon$

وبالتالي، من خلال تطبيق معيار المربعات الصغرى ، يمكننا الوصول إلى صيغة تقدير معاملات نموذج الانحدار متعدد الحدود :

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

ومع ذلك، فإن إجراء هذه الحسابات يدويًا أمر شاق للغاية ويستغرق وقتًا طويلاً، لذا فمن الملائم أكثر استخدام برامج الكمبيوتر (مثل Minitab أو Excel) التي تتيح لك تنفيذ نموذج انحدار متعدد الحدود بشكل أسرع بكثير.

مثال على نموذج الانحدار متعدد الحدود

الآن بعد أن عرفنا تعريف الانحدار متعدد الحدود وكيفية تنفيذه، دعونا نلقي نظرة على مثال واقعي لفهم المفهوم بشكل كامل.

أولا وقبل كل شيء، يجب أن نأخذ في الاعتبار أنه ينبغي تنفيذ نموذج الانحدار متعدد الحدود عندما يكون الرسم البياني للبيانات على شكل منحنى متعدد الحدود. على سبيل المثال، إذا كانت النقطة النقطية على شكل منحنى مكعب، فنحن بحاجة إلى إنشاء نموذج انحدار متعدد الحدود من الدرجة الثالثة.

لذا، كما ترون في الصورة التالية، فإن المخطط النقطي لبياناتنا له شكل تربيعي، لأنه كلما قمنا بزيادة قيمة المتغير المستقل، ينمو المتغير التابع بشكل أسرع. في هذه الحالة تم تنفيذ نموذج الانحدار الخطي وكما ترون فهو لا يتناسب مع النقاط بشكل جيد لأنه يحتوي على أقسام يكون فيها الخط أسفل جميع النقاط وأقسام يكون فيها الخط فوقها.

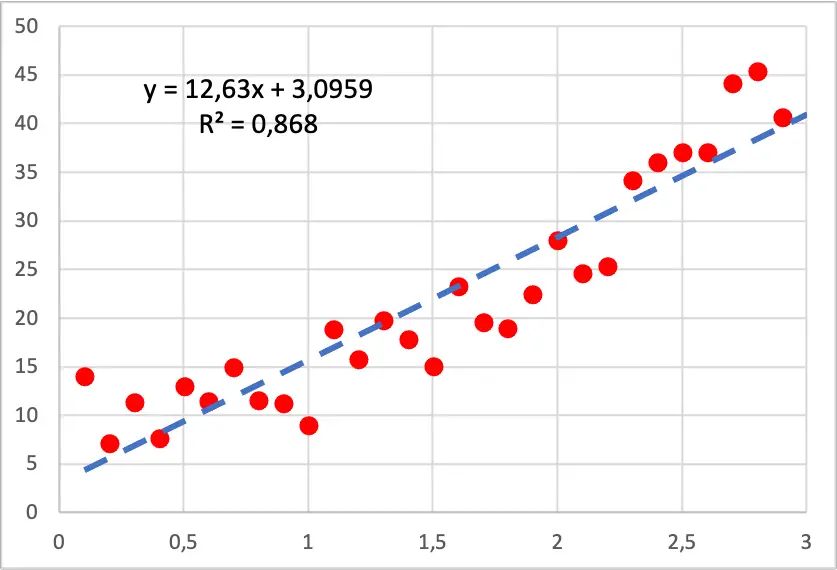
من ناحية أخرى، إذا قمنا بتشغيل نموذج انحدار متعدد الحدود من الدرجة الثانية، فإنه يناسب بيانات العينة بشكل أفضل، كما ترون في الصورة أدناه.

بالإضافة إلى ذلك، عند تطوير نموذج الانحدار متعدد الحدود، تحسن معامل التحديد بشكل كبير حيث انتقل من 86.80% إلى 94.05%. ولذلك، فإن نموذج الانحدار الجديد يشرح مجموعة البيانات بشكل أفضل.

من ناحية أخرى، هناك إشارة أخرى إلى أننا بحاجة إلى إجراء انحدار متعدد الحدود وهو رسم البقايا. إذا كان الرسم البياني للبقايا في الانحدار الخطي على شكل قطع مكافئ أو نوع آخر من كثيرات الحدود، فإن نموذج الانحدار متعدد الحدود يناسب بالتأكيد البيانات التي تمت دراستها بشكل أفضل.

أنواع أخرى من الانحدار غير الخطي

هناك ثلاثة أنواع رئيسية من الانحدار غير الخطي:

الانحدار متعدد الحدود – معادلة نموذج الانحدار هي في شكل كثير الحدود.
الانحدار اللوغاريتمي : يتم أخذ لوغاريتم المتغير المستقل.
الانحدار الأسي : المتغير المستقل موجود في أس المعادلة.

➤ انظر: الانحدار اللوغاريتمي
➤ انظر: الانحدار الأسي

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر