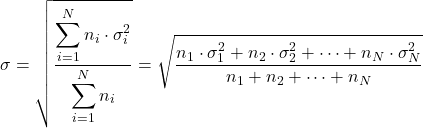الانحراف المعياري (أو الانحراف المعياري)

By دكتور بنيامين أندرسون زومار 5, 2023 إحصائيات 0 Comments

تشرح هذه المقالة ما هو الانحراف المعياري، والذي يسمى أيضًا الانحراف المعياري. سوف تتعلم كيفية حساب الانحراف المعياري، ومثال عملي خطوة بخطوة وآلة حاسبة عبر الإنترنت للعثور على الانحراف المعياري لأي عينة بيانات.

ما هو الانحراف المعياري (أو الانحراف المعياري)؟

الانحراف المعياري ، ويسمى أيضًا الانحراف المعياري ، هو مقياس للتشتت الإحصائي. وبعبارة أخرى، الانحراف المعياري هو القيمة التي تشير إلى تشتت مجموعة من البيانات الإحصائية.

ولذلك، يتم استخدام الانحراف المعياري (أو الانحراف المعياري) لقياس تشتت السكان أو العينة الإحصائية. كلما زاد الانحراف المعياري لسلسلة البيانات، زادت تشتت البيانات. ويمكن أيضًا أن يتم التفسير في الاتجاه الآخر، فإذا كان الانحراف المعياري منخفضًا فهذا يعني أن البيانات بشكل عام قريبة جدًا من متوسطها.

عند حساب الانحراف المعياري أو النموذجي على مجتمع ما، فإن رمز الانحراف المعياري هو الحرف اليوناني سيجما (σ). ولكن عندما يتعلق الأمر بعينة الانحراف المعياري، يتم استخدام الحرف s لتمثيل القياس الإحصائي.

في بعض كتب الإحصاء والاحتمالات، يُسمى الانحراف المعياري أيضًا بالانحراف المعياري.

صيغة الانحراف المعياري (أو الانحراف المعياري).

الانحراف المعياري (أو الانحراف المعياري) يساوي الجذر التربيعي لمجموع مربعات انحرافات سلسلة البيانات مقسومًا على إجمالي عدد الملاحظات.

وبالتالي فإن صيغة حساب الانحراف المعياري (أو الانحراف المعياري) هي:

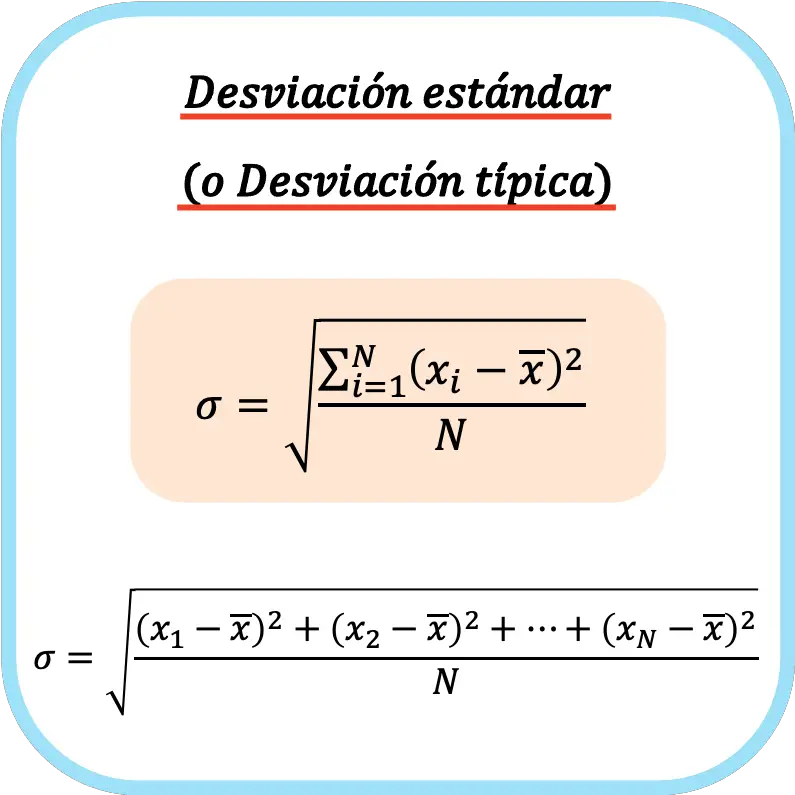
👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب الانحراف المعياري لأي مجموعة بيانات.

In conclusion, to find the standard deviation of a data set, you need to calculate all the deviations (defined as the difference between a data point and the arithmetic mean), increase the deviations to two, add them all up, then divide by the مجموع. عدد البيانات، وأخيرًا خذ الجذر التربيعي.

مثال على الانحراف المعياري (أو الانحراف المعياري)

بالنظر إلى تعريف الانحراف المعياري (أو الانحراف النموذجي)، يوجد أدناه مثال خطوة بخطوة حتى تتمكن من معرفة كيفية حساب الانحراف المعياري لسلسلة البيانات.

احسب الانحراف المعياري للقيم التالية: 3، 6، 2، 9، 4.

أول شيء يتعين علينا القيام به هو تحديد متوسط العينة. للقيام بذلك، نقوم بجمع كافة البيانات وتقسيمها على إجمالي عدد الملاحظات، وهو خمسة:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

نستخدم الآن صيغة الانحراف المعياري:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

نعوض البيانات في الصيغة:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

وأخيرا نحسب الانحراف المعياري:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

حاسبة الانحراف المعياري (أو الانحراف المعياري).

أدخل مجموعة من البيانات الإحصائية في الآلة الحاسبة الإلكترونية التالية لحساب انحرافها المعياري (أو الانحراف المعياري). يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.

الانحراف المعياري (أو النموذجي) للبيانات المجمعة

لحساب الانحراف المعياري (أو الانحراف المعياري) للبيانات المجمعة في فترات ، يجب اتباع الخطوات التالية:

أوجد متوسط البيانات المجمعة.
حساب انحرافات البيانات المجمعة.
قم بتربيع كل فجوة.
اضرب كل نتيجة سابقة في تكرار الفاصل الزمني لها.
أضف مجموع كل القيم التي تم الحصول عليها في الخطوة السابقة.
قسّم على العدد الإجمالي للملاحظات.
خذ الجذر التربيعي للقيمة السابقة. الرقم الناتج هو الانحراف المعياري للبيانات المجمعة.

في الختام، فإن صيغة حساب الانحراف المعياري للبيانات المجمعة في فترات هي:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

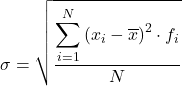
على الرغم من أن الصيغة المذكورة أعلاه تستخدم عادة، إلا أنه يمكن استخدام التعبير الجبري التالي أيضًا حيث يتم الحصول على نفس النتيجة:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

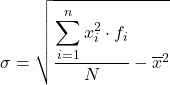
حتى تتمكن من رؤية كيفية القيام بذلك، فيما يلي تمرين خطوة بخطوة حول الانحراف المعياري للبيانات المجمعة في فواصل زمنية. وبتعبير أدق، سيتم حساب الانحراف المعياري للبيانات الإحصائية التالية:

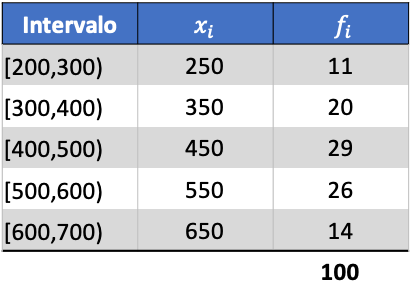
أولاً، نضرب درجة الفصل لكل فترة في تكرارها لحساب المتوسط الحسابي:

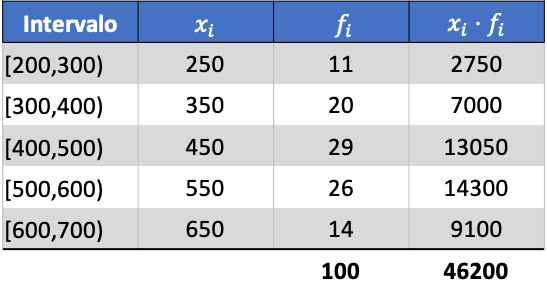
وبالتالي فإن متوسط البيانات المجمعة سيكون:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

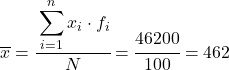
الآن بعد أن عرفنا قيمة المتوسط، نحتاج إلى إضافة الأعمدة الثلاثة التالية إلى جدول البيانات:

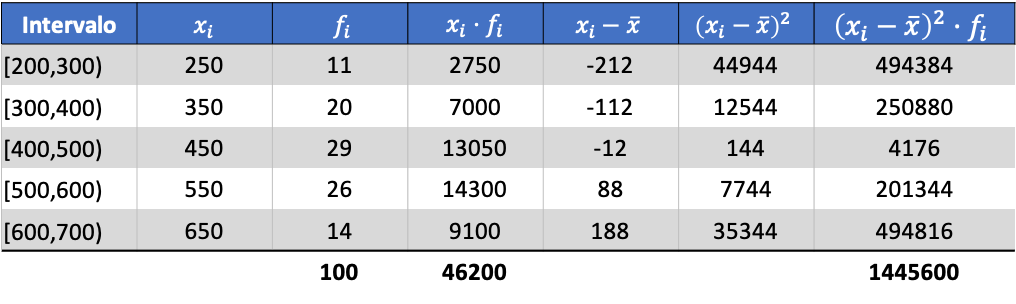
حل تمرين الانحراف المعياري أو الانحراف المعياري للبيانات المجمعة

سيكون الانحراف المعياري للبيانات المجمعة نتيجة الجذر التربيعي لإجمالي العمود الأخير مقسومًا على إجمالي عدد الملاحظات:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

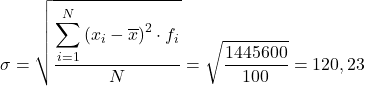
الانحراف والتباين القياسي (أو النموذجي).

العلاقة بين الانحراف المعياري (أو الانحراف النموذجي) والتباين هو أن الانحراف المعياري هو الجذر التربيعي للتباين.

لذا، إذا كنا نعرف قيمة التباين لمجموعة بيانات، فيمكننا بسهولة حساب الانحراف المعياري عن طريق أخذ الجذر التربيعي. أو على العكس من ذلك، إذا عرفنا الانحراف المعياري، فيمكننا إيجاد التباين بتربيع القيمة.

$Var(X)=\sigma^2$

في الواقع، يمكن تمثيل التباين ببساطة باستخدام رمز الانحراف المعياري المربع. ولذلك فإن رمز تباين السكان هو مربع سيجما (σ ² ) ورمز تباين العينة هو s مربع (s ² ).

بالإضافة إلى ذلك، فإن مفهومي الانحراف المعياري والتباين لهما تفسير مماثل، حيث أن كلاهما يظهر تشتت سلسلة من البيانات الإحصائية.

خصائص الانحراف المعياري (أو الانحراف المعياري)

الانحراف المعياري له الخصائص التالية:

لا يمكن أن يكون الانحراف المعياري لعينة البيانات سالبًا.

$\sigma \ge 0$

سيكون الانحراف المعياري صفرًا إذا كانت جميع البيانات متماثلة.

$\sigma =0$

إذا تمت إضافة مصطلح ثابت إلى جميع البيانات، فلن تتغير قيمة الانحراف المعياري.

$\sigma (X+k)=\sigma (X)$

إذا تم ضرب جميع البيانات برقم، فسيتم ضرب الانحراف المعياري بالقيمة المطلقة للرقم المذكور.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

الانحراف المعياري لمجموع متغيرين عشوائيين يساوي الجذر التربيعي لمجموع تباينات المتغيرات بالإضافة إلى ضعف التباين بين المتغيرين.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

إذا عرفنا الانحرافات المعيارية للتوزيعات المختلفة (σ _i ) وعدد بياناتها (n _i ) فيمكننا حساب الانحراف المعياري الإجمالي بتطبيق الصيغة التالية:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر