الانحدار من خلال الأصل: التعريف والمثال

الانحدار الخطي البسيط هو أسلوب يمكن استخدامه لقياس العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .

يأخذ نموذج الانحدار الخطي البسيط الشكل التالي:

ص = β ₀ + β ₁ س

ذهب:

• y : قيمة متغير الاستجابة
• β ₀ : قيمة متغير الاستجابة عندما يكون x = 0 (يُسمى مصطلح “الاعتراض”)
• β ₁ : متوسط الزيادة في متغير الاستجابة المرتبط بزيادة وحدة واحدة في x
• x : قيمة المتغير التنبؤي

تُعرف النسخة المعدلة من هذا النموذج باسم الانحدار من خلال الأصل ، والذي يجبر y على أن يساوي 0 عندما يكون x يساوي 0.

ويأخذ هذا النوع من النماذج الشكل التالي:

ص = _β1x

لاحظ أنه تمت إزالة مصطلح التقاطع بالكامل من النموذج.

يُستخدم هذا النموذج أحيانًا عندما يعلم الباحثون أن متغير الاستجابة يجب أن يكون صفرًا عندما يكون المتغير المتوقع صفرًا.

في العالم الحقيقي، يُستخدم هذا النوع من النماذج غالبًا في الدراسات الحرجية أو البيئية .

على سبيل المثال، يمكن للباحثين استخدام محيط الشجرة للتنبؤ بارتفاع الشجرة. إذا كان محيط الشجرة صفرًا، فيجب أن يكون ارتفاعها صفرًا.

لذلك، عند ملاءمة نموذج الانحدار لهذه البيانات، لن يكون من المنطقي أن يكون المصطلح الأصلي غير صفري.

يوضح المثال التالي الفرق بين تركيب نموذج الانحدار الخطي البسيط العادي والنموذج الذي ينفذ الانحدار عبر الأصل.

مثال: الانحدار من خلال الأصل

لنفترض أن عالم الأحياء يريد ملاءمة نموذج الانحدار باستخدام محيط الشجرة للتنبؤ بارتفاع الشجرة. خرجت وجمعت القياسات التالية لعينة مكونة من 15 شجرة:

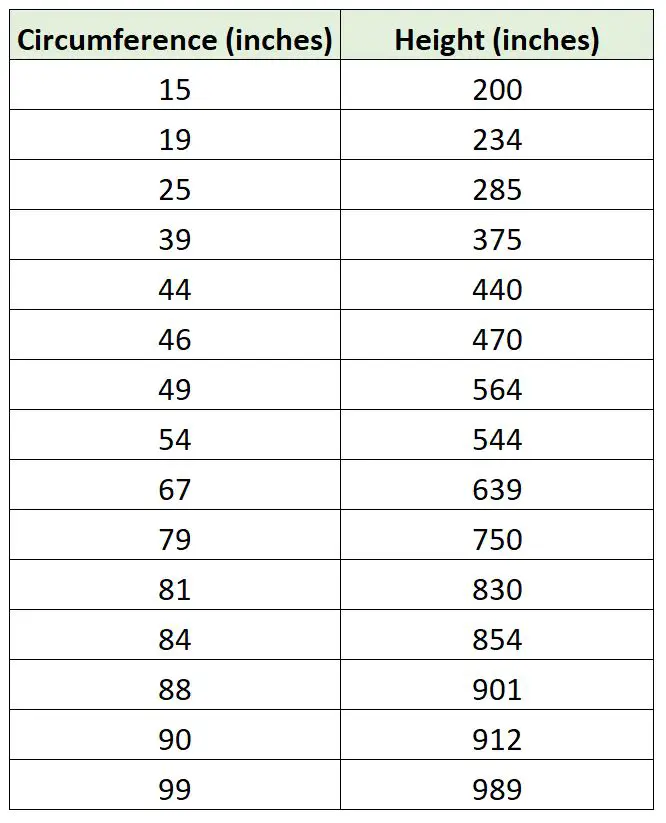
يمكننا استخدام الكود التالي في R لتناسب نموذج الانحدار الخطي البسيط مع نموذج الانحدار الذي لا يستخدم أي اعتراضات ويرسم خطي الانحدار:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

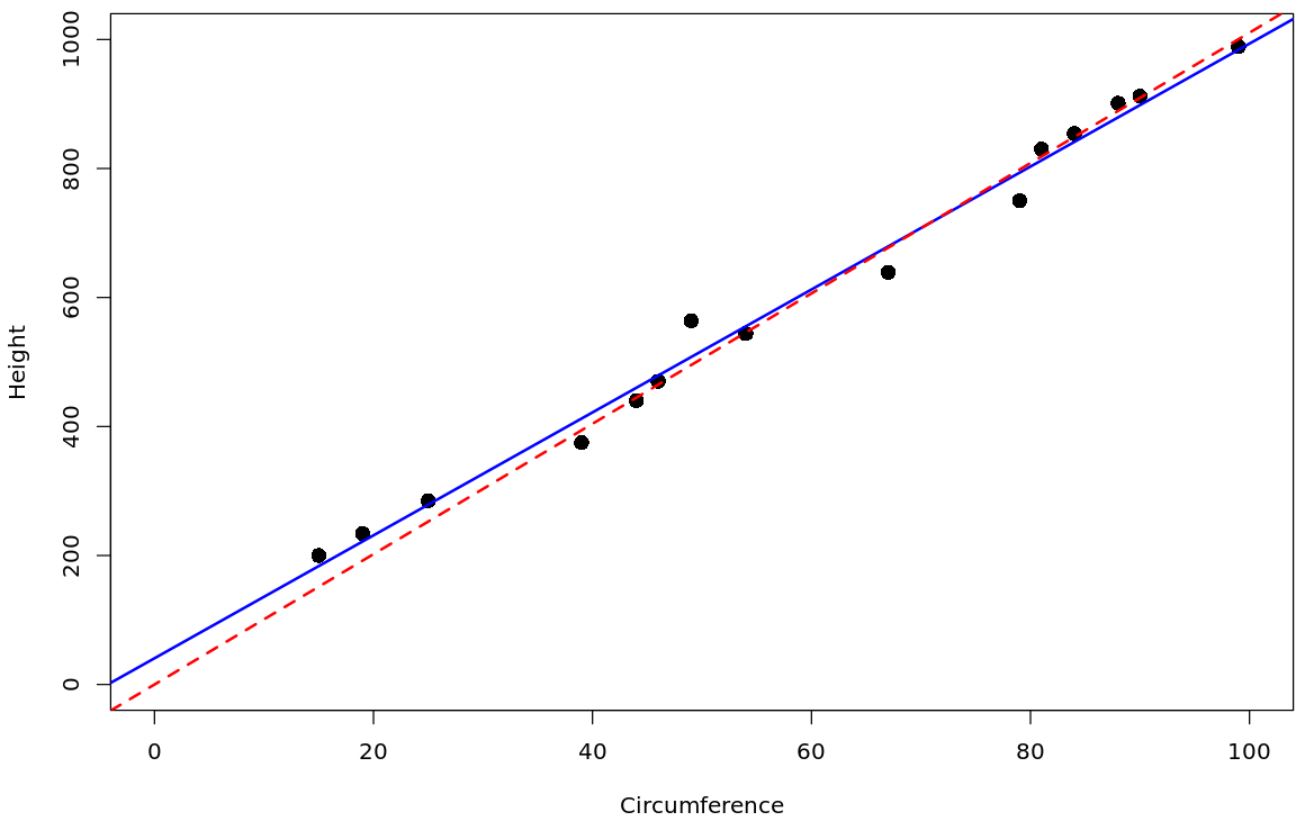
يمثل الخط الأحمر المنقط نموذج الانحدار الذي يمر عبر نقطة الأصل، ويمثل الخط الأزرق الصلب نموذج الانحدار الخطي البسيط العادي.

يمكننا استخدام الكود التالي في R للحصول على تقديرات المعامل لكل نموذج:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

المعادلة المجهزة لنموذج الانحدار الخطي البسيط هي:

الارتفاع = 40.6969 + 9.5296 (المحيط)

والمعادلة الملائمة لنموذج الانحدار عبر نقطة الأصل هي:

الارتفاع = 10.1057 (المحيط)

لاحظ أن تقديرات المعامل لمتغير المحيط تختلف قليلاً.

احتياطات لاستخدام الانحدار عبر الأصل

قبل استخدام انحدار التقاطع، يجب أن تكون متأكدًا تمامًا من أن القيمة 0 لمتغير التوقع تتضمن قيمة 0 لمتغير الاستجابة. في العديد من السيناريوهات، يكاد يكون من المستحيل معرفة ذلك على وجه اليقين.

وإذا كنت تستخدم الانحدار عبر الأصل لتوفير درجة من الحرية في تقدير الأصل، فإنه نادرًا ما يحدث فرقًا كبيرًا إذا كان حجم عينتك كبيرًا بدرجة كافية.

إذا اخترت استخدام الانحدار عبر الأصل، فتأكد من توضيح أسبابك في التحليل النهائي أو التقرير.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول الانحدار الخطي:

مقدمة إلى الانحدار الخطي البسيط
مقدمة في الانحدار الخطي المتعدد
كيفية قراءة وتفسير جدول الانحدار