التوزيع الطبيعي
تشرح هذه المقالة ما هو التوزيع الطبيعي في الإحصائيات. لذا ستجد تعريف التوزيع الطبيعي وأمثلة على التوزيع الطبيعي وما هي خصائص التوزيع الطبيعي.
ما هو التوزيع الطبيعي؟
التوزيع الطبيعي هو توزيع احتمالي مستمر يكون رسمه البياني على شكل جرس ومتماثل حول متوسطه. في الإحصاء، يُستخدم التوزيع الطبيعي لنمذجة الظواهر ذات الخصائص المختلفة جدًا، ولهذا السبب يعد هذا التوزيع مهمًا جدًا.
في الواقع، في الإحصاء، يعتبر التوزيع الطبيعي هو التوزيع الأكثر أهمية على الإطلاق لجميع التوزيعات الاحتمالية، لأنه لا يمكنه فقط وضع نموذج لعدد كبير من ظواهر العالم الحقيقي، ولكن يمكن أيضًا استخدام التوزيع الطبيعي لتقريب أنواع أخرى من الظواهر. توزيعات. تحت ظروف معينة.
رمز التوزيع الطبيعي هو الحرف الكبير N. لذا، للإشارة إلى أن المتغير يتبع التوزيع الطبيعي، تتم الإشارة إليه بالحرف N وتضاف قيم وسطه الحسابي وانحرافه المعياري بين قوسين.
![]()
للتوزيع الطبيعي العديد من الأسماء المختلفة، بما في ذلك التوزيع الغاوسي ، والتوزيع الغاوسي ، وتوزيع لابلاس-غاوس .
أمثلة على التوزيعات العادية
عادةً، تحتوي مجموعات البيانات التي تتبع التوزيع الطبيعي على عدد كبير من الملاحظات وتغطي موضوعات عامة جدًا. فيما يلي عدة أمثلة للعينات الإحصائية التي يمكن نمذجتها عمومًا بالتوزيع الطبيعي.
أمثلة على التوزيع الطبيعي:
- حجم الطلاب في الدورة.
- معدل الذكاء للعاملين في الشركة.
- عدد الأجزاء المعيبة التي ينتجها المصنع في يوم واحد.
- الدرجات التي حصل عليها الطلاب في الامتحان في المقرر الدراسي.
- ربحية أسهم الشركات المدرجة في البورصة.
الرسم البياني للتوزيع الطبيعي
بعد أن رأينا ما هو التوزيع الطبيعي وبعض الأمثلة على هذا النوع من التوزيع الاحتمالي، دعونا نرى كيف يبدو الرسم البياني الخاص به لفهم المفهوم بشكل أفضل.
في الرسم البياني التالي، يمكنك أن ترى كيف تختلف دالة الكثافة للتوزيع الطبيعي باختلاف قيم وسطها الحسابي وانحرافها المعياري.
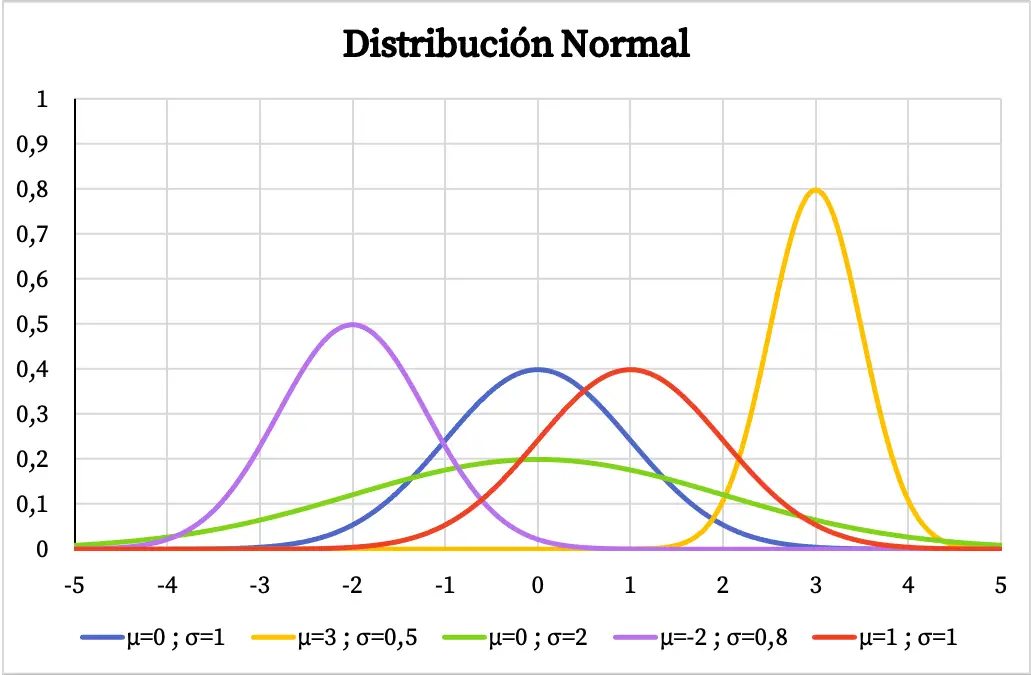
وجود شكل جرس متمركز حول الوسط الحسابي، إذا كان للمتغير توزيع طبيعي فهذا يعني أن القيمة الأكثر تكرارًا هي المتوسط وأن القيم حول المتوسط تتكرر بشكل متكرر أكثر من القيم المتطرفة. وبالمثل، كلما زاد الانحراف المعياري للتوزيع الطبيعي، أصبح شكل تمثيله البياني أكثر استواءً.
ومن ناحية أخرى فإن الرسم البياني لدالة الاحتمالية التراكمية للتوزيع الطبيعي يعتمد أيضًا على قيم وسطها الحسابي وانحرافها المعياري، كما ترون في الصورة التالية:
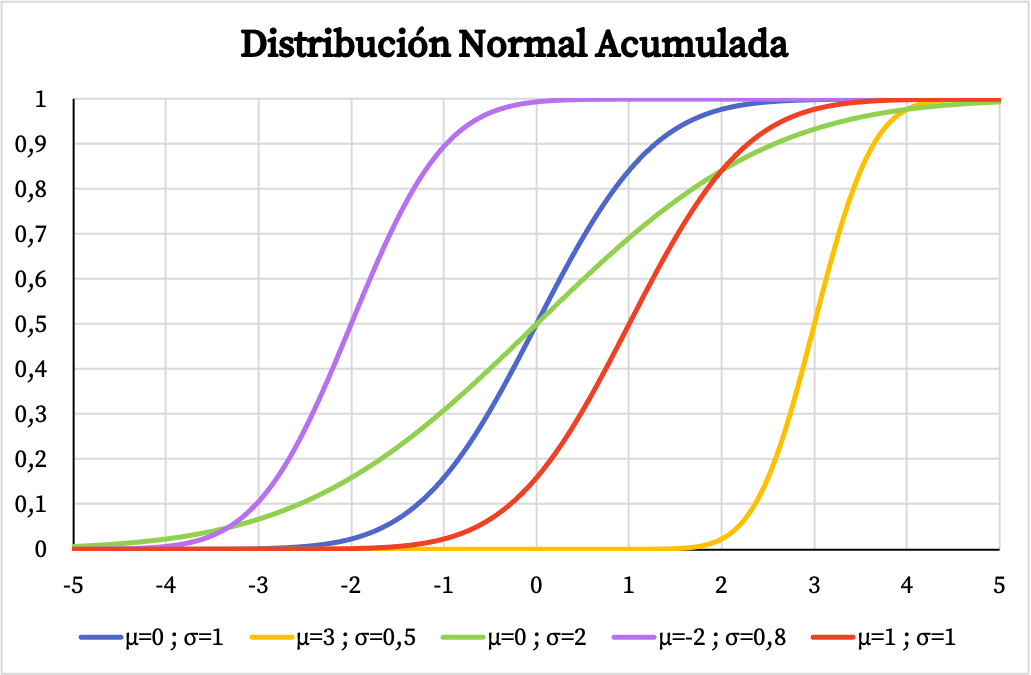
تتيح دالة الكثافة ودالة التوزيع للتوزيع الطبيعي حساب الاحتمالات المرتبطة بهذا التوزيع. ومع ذلك، بدلاً من استخدام صيغها، يمكنك استخدام جداول التوزيع العادية مباشرة لأنها أسرع. ويمكن الاطلاع على هذه الجداول على الرابط التالي:
خصائص التوزيع الطبيعي
يتميز التوزيع الطبيعي بالخصائص التالية:
- يعتمد التوزيع الطبيعي على معلمتين مميزتين، وهما وسطه الحسابي (μ) وانحرافه المعياري (σ).
![]()
- يمكن أن يأخذ التوزيع الطبيعي قيمًا موجبة وسالبة، وبالتالي فإن مجال التوزيع الطبيعي يتكون من أرقام حقيقية.
![]()
- الوسيط وطريقة التوزيع الطبيعي يساويان الوسط الحسابي للتوزيع.
![]()
- معامل التواء ومعامل التفرطح للتوزيع الطبيعي يساوي صفر.
![]()
- صيغة دالة الكثافة للتوزيع الطبيعي هي:
![]()
- وبالمثل، فإن صيغة دالة الاحتمال التراكمي للتوزيع الطبيعي هي:
![]()
- أحد تطبيقات نظرية الحد المركزي هو أن توزيع بواسون يمكن أن يقترب من التوزيع الطبيعي عندما تكون قيمة lect كبيرة بما فيه الكفاية.
![]()
- تطبيق آخر لنظرية الحد المركزي هو أنه يمكن تقريب التوزيع ذي الحدين عن طريق التوزيع الطبيعي لمجموعات البيانات التي تحتوي على عدد كبير من الملاحظات.
![]()
التوزيع القياسي
التوزيع الطبيعي القياسي ، ويسمى أيضًا التوزيع الطبيعي للوحدة ، هو أبسط حالة للتوزيع الطبيعي. بتعبير أدق، التوزيع الطبيعي القياسي هو توزيع طبيعي بقيم متوسط وانحراف معياري يساوي 0 و1 على التوالي.
![Rendered by QuickLaTeX.com \displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ca26cb58ac445099df12aeebda27e38_l3.png)
لاحظ أنه يمكن تحويل أي توزيع طبيعي إلى توزيع طبيعي قياسي من خلال تطبيق عملية تسمى الكتابة، والتي تتضمن طرح متوسطها الحسابي من كل قيمة ثم القسمة على انحرافها المعياري.
بالإضافة إلى ذلك، يتم استخدام التوزيع الطبيعي القياسي لتحديد أي احتمال للتوزيع الطبيعي باستخدام جدول الاحتمالات الخاص به. لذلك، للعثور على احتمال التوزيع الطبيعي، يتم إدخال المتغير أولاً لتحويله إلى توزيع عادي قياسي، ثم ننظر في الجدول لنرى ما هي قيمة الاحتمال المقابلة. لمعرفة المزيد اضغط على الرابط التالي:
التوزيع الطبيعي والقاعدة التجريبية
في الإحصاء، القاعدة العامة ، وتسمى أيضًا قاعدة 68-95-99.7 ، هي قاعدة تحدد النسبة المئوية للقيم في التوزيع الطبيعي التي تقع ضمن ثلاثة انحرافات معيارية عن المتوسط.
وبشكل أكثر تحديدًا، تنص القاعدة العامة على ما يلي:
- 68% من القيم في التوزيع الطبيعي تقع ضمن انحراف معياري واحد عن الوسط.
- 95% من القيم في التوزيع الطبيعي تقع ضمن انحرافين معياريين عن المتوسط.
- 99.7% من القيم في التوزيع الطبيعي تقع ضمن ثلاثة انحرافات معيارية عن المتوسط.
