كيفية محاكاة ورسم التوزيع الطبيعي ثنائي المتغير في r

في الإحصاء، يتبع متغيران التوزيع الطبيعي ثنائي المتغير إذا كان لهما توزيع طبيعي عند إضافتهما معًا.

يشرح هذا البرنامج التعليمي كيفية تنفيذ المهام التالية في R:

• محاكاة التوزيع الطبيعي ثنائي المتغير
• رسم التوزيع الطبيعي ثنائي المتغير باستخدام مخطط كفاف (مخطط ثنائي الأبعاد)
• رسم التوزيع الطبيعي ثنائي المتغير باستخدام قطعة أرض (مؤامرة ثلاثية الأبعاد)

دعنا نذهب!

مثال 1: محاكاة التوزيع الطبيعي ثنائي المتغير في R

إن أبسط طريقة لمحاكاة التوزيع الطبيعي ثنائي المتغير في R هي استخدام الدالة mvrnorm() من الحزمة MASS .

يوضح الكود التالي كيفية استخدام هذه الوظيفة لمحاكاة التوزيع الطبيعي ثنائي المتغير عمليًا:

 library (MASS)

#make this example reproducible
set. seed ( 0 )

#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238

إليك ما تفعله كل وسيطة للدالة mvrnorm() :

• n : يحدد حجم العينة
• mu : يحدد متوسط كل متغير
• سيجما : يحدد مصفوفة التباين للمتغيرين

والنتيجة النهائية هي إطار بيانات بمتغيرين يتبعان التوزيع الطبيعي عند إضافتهما معًا.

المثال 2: رسم التوزيع الطبيعي ثنائي المتغير

أسهل طريقة لرسم التوزيع الطبيعي ثنائي المتغير في لغة R هي استخدام الوظائف الموجودة في الحزمة mnormt() .

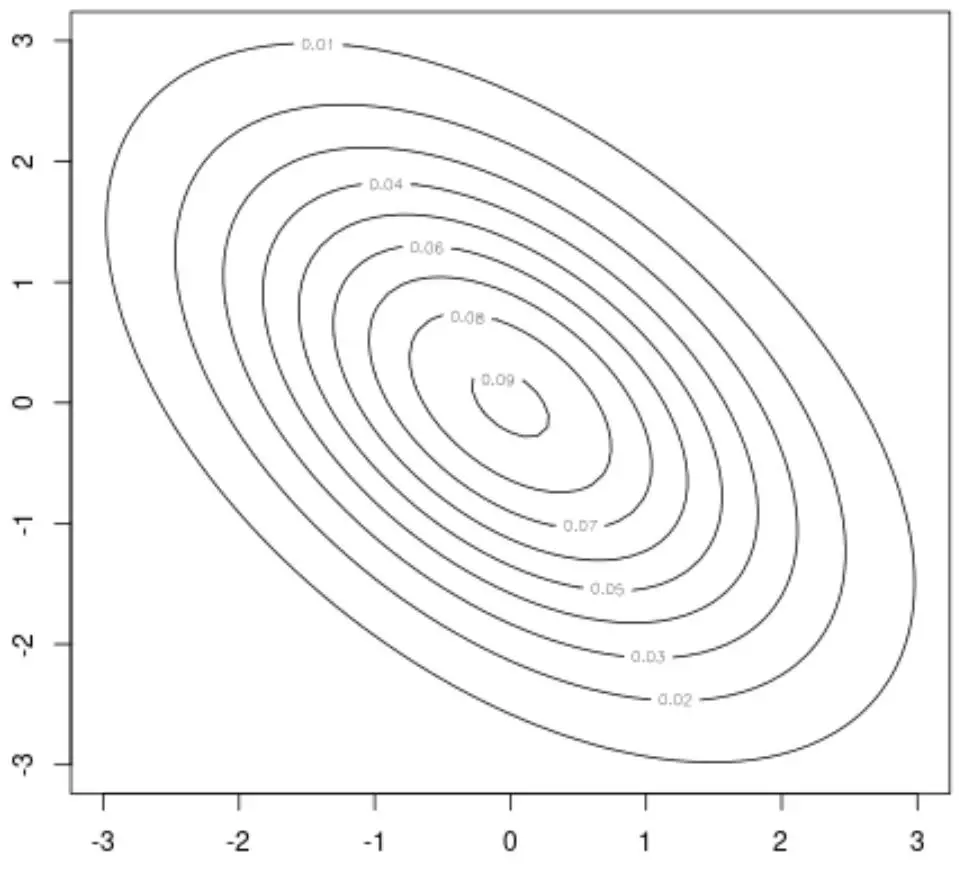
على سبيل المثال، يمكننا استخدام الدالة الكنتورية () لهذه الحزمة لإنشاء مخطط كفاف، والذي يوفر تصورًا ثنائي الأبعاد للتوزيع الطبيعي ثنائي المتغير:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create contour plot
contour(x, y, z)

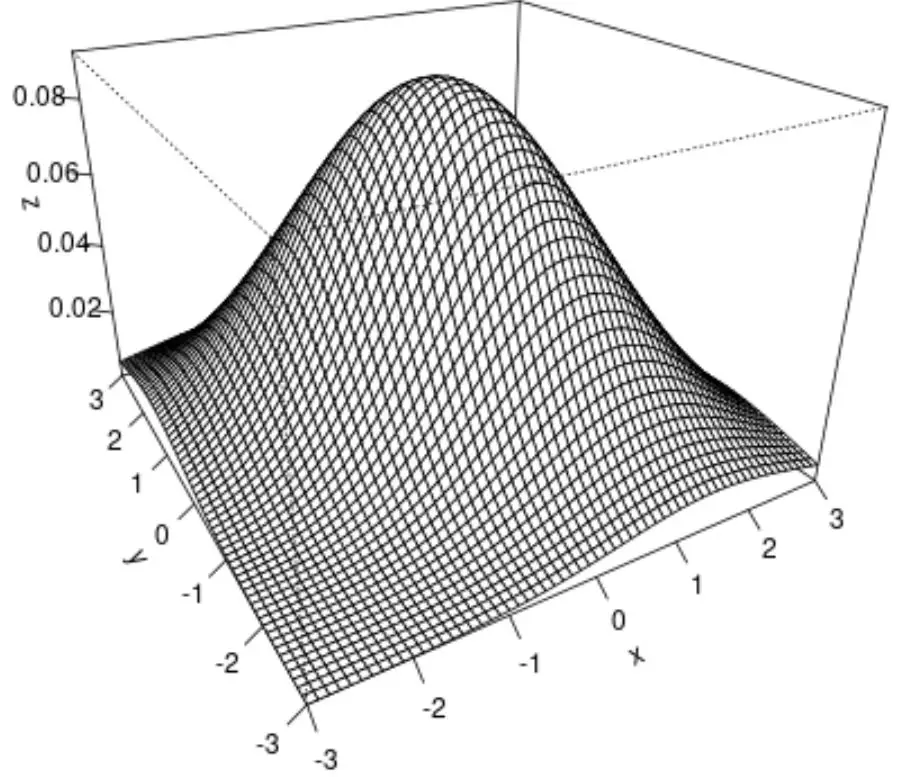
يمكننا أيضًا استخدام الدالة persp() لإنشاء مخطط سطحي، والذي يوفر تصورًا ثلاثي الأبعاد للتوزيع الطبيعي ثنائي المتغير:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')

إليك ما تفعله كل وسيطة للدالة persp() :

• ثيتا، فاي : يضبط زوايا اتجاه العرض.
• توسيع : التحكم في حجم المحور ع.
• Ticktype : يتحكم في ظهور علامات التجزئة على المحاور.

والنتيجة النهائية هي مؤامرة سطحية ثلاثية الأبعاد للتوزيع الطبيعي ثنائي المتغير.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية استخدام التوزيعات الاحتمالية الأخرى في R:

كيفية استخدام التوزيع الطبيعي في R
كيفية استخدام التوزيع ذي الحدين في R
كيفية استخدام توزيع بواسون في R
كيفية استخدام التوزيع متعدد الحدود في R