التوزيع الطبيعي

التوزيع الطبيعي هو التوزيع الاحتمالي الأكثر شيوعا في الإحصاء.

التوزيعات الطبيعية لها الخصائص التالية:

• شكل الجرس
• متماثل
• المتوسط والوسيط متساويان؛ وكلاهما يقع في وسط التوزيع
• يقع حوالي 68% من البيانات ضمن انحراف معياري واحد عن المتوسط
• يقع حوالي 95% من البيانات ضمن انحرافين معياريين عن المتوسط.
• يقع حوالي 99.7% من البيانات ضمن ثلاثة انحرافات معيارية عن المتوسط.

تُعرف النقاط الثلاث الأخيرة بالقاعدة العامة ، والتي تسمى أحيانًا بقاعدة 68-95-99.7 .

ذات صلة: القاعدة العامة (قضايا الممارسة)

كيفية رسم منحنى عادي

لرسم منحنى عادي، علينا معرفة المتوسط والانحراف المعياري.

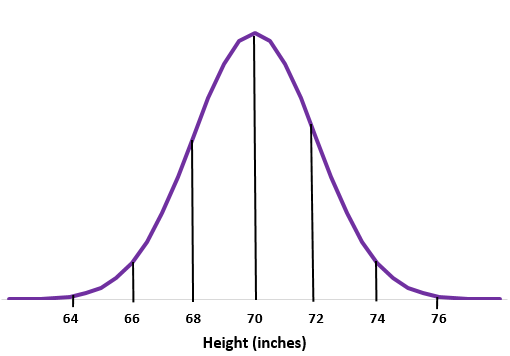
مثال 1: لنفترض أن طول الرجال في مدرسة معينة يتم توزيعه بشكل طبيعي بمتوسط $\mu =\; 70\; بوصة\; وانحراف$ معياري قدره $\sigma \; =\; 2\; بوصة.\; رسم\; المنحنى\; العادي.$

الخطوة 1: رسم منحنى عادي.

الخطوة 2: متوسط 70 بوصة في المنتصف.

الخطوة 3: كل انحراف معياري يتوافق مع مسافة 2 بوصة.

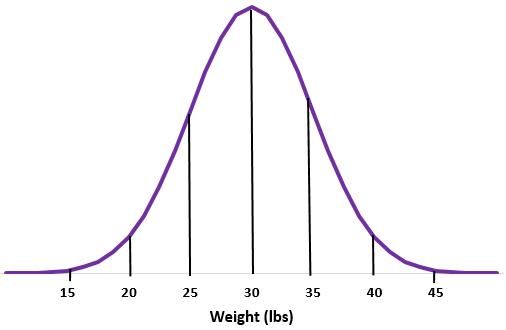
مثال 2: لنفترض أن وزن نوع معين من ثعالب الماء يتم توزيعه بشكل طبيعي بمتوسط $\mu =\; 30\; رطل\; وانحراف$ معياري قدره $\sigma \; =\; 5\; رطل.\; رسم\; المنحنى\; العادي.$

الخطوة 1: رسم منحنى عادي.

الخطوة 2: يقع متوسط الـ 30 رطلاً في المنتصف.

الخطوة 3: كل انحراف معياري يتوافق مع مسافة 5 رطل

كيفية إيجاد النسب المئوية باستخدام التوزيع الطبيعي

القاعدة الأساسية ، والتي تسمى أحيانًا قاعدة 68-95-99.7 ، تنص على أنه بالنسبة للمتغير العشوائي الموزع بشكل طبيعي، فإن 68% من البيانات تقع ضمن نطاق انحراف معياري واحد عن المتوسط، و95% تقع ضمن نطاق معيارين انحرافات عن المتوسط و 99.7% تقع ضمن ثلاثة انحرافات معيارية عن المتوسط.

باستخدام هذه القاعدة يمكننا الإجابة على الأسئلة المتعلقة بالنسب المئوية.

مثال: لنفترض أن طول الرجال في مدرسة معينة يتم توزيعه بشكل طبيعي بمتوسط $\mu =\; 70\; بوصة\; وانحراف$ معياري قدره $\sigma \; =\; 2\; بوصة.$

$ما\; هي\; النسبة\; المئوية\; تقريبًا\; للرجال\; في\; هذه\; المدرسة\; الذين\; يزيد\; طولهم\; عن\; 74\; بوصة؟$

حل:

الخطوة 1: رسم التوزيع الطبيعي بمتوسط $\mu =\; 70\; بوصة\; وانحراف$ معياري قدره $\sigma \; =\; 2\; بوصة.$

الخطوة 2: ارتفاع 74 بوصة هو انحرافان معياريان عن المتوسط. أضف النسب المئوية فوق هذه النقطة إلى التوزيع الطبيعي.

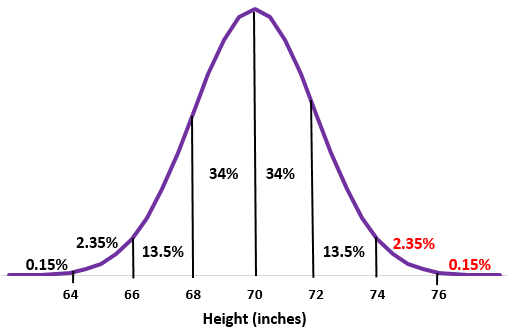
2.35% + 0.15% = 2.5%

يبلغ طول حوالي 2.5% من الرجال في هذه المدرسة أكثر من 74 بوصة.

$ما\; هي\; النسبة\; المئوية\; تقريبًا\; للرجال\; في\; هذه\; المدرسة\; الذين\; يتراوح\; طولهم\; بين\; 68\; بوصة\; و72\; بوصة؟$

حل:

الخطوة 1: رسم التوزيع الطبيعي بمتوسط $\mu =\; 70\; بوصة\; وانحراف$ معياري قدره $\sigma \; =\; 2\; بوصة.$

الخطوة 2: ارتفاع 68 بوصة و72 بوصة هو انحراف معياري واحد أقل من المتوسط وفوقه، على التوالي. ما عليك سوى إضافة النسب المئوية بين هاتين النقطتين في التوزيع الطبيعي.

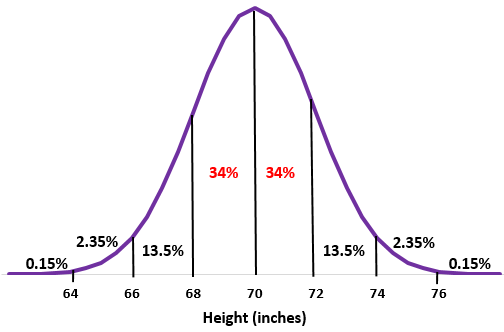
34% + 34% = 68%

يتراوح طول حوالي 68% من الرجال في هذه المدرسة بين 68 بوصة و72 بوصة.

كيفية العثور على الأعداد باستخدام التوزيع الطبيعي

يمكننا أيضًا استخدام القاعدة العامة للإجابة عن الأسئلة المتعلقة بالأعداد.

مثال: لنفترض أن وزن نوع معين من ثعالب الماء يتم توزيعه بشكل طبيعي بمتوسط $\mu =\; 30\; رطل\; وانحراف$ معياري قدره $\sigma \; =\; 5\; رطل.$

مستعمرة معينة لديها 200 من هذه ثعالب الماء. كم عدد ثعالب الماء التي تزن أكثر من 35 رطلاً تقريبًا؟

حل:

الخطوة 1: رسم التوزيع الطبيعي بمتوسط $\mu =\; 30\; رطل\; وانحراف$ معياري قدره $\sigma \; =\; 5\; رطل.$

الخطوة 2: الوزن 35 رطلاً هو انحراف معياري واحد فوق المتوسط. أضف النسب المئوية فوق هذه النقطة إلى التوزيع الطبيعي.

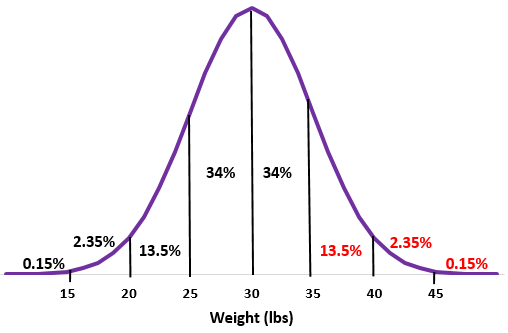
13.5% + 2.35% + 0.15% = 16%

الخطوة 3: بما أن هناك 200 ثعالب ماء في المستعمرة، 16% من 200 = 0.16 * 200 = 32

يبلغ وزن حوالي 32 ثعالب الماء في هذه المستعمرة أكثر من 35 رطلاً.

كم عدد ثعالب الماء تقريبًا في هذه المستعمرة التي يقل وزنها عن 30 رطلاً؟

بدلًا من اتباع جميع الخطوات التي اتخذناها أعلاه، يمكننا أن ندرك أن متوسط التوزيع الطبيعي يساوي المتوسط، وهو 30 رطلاً في هذه الحالة.

وهذا يعني أن نصف ثعالب الماء يزن أكثر من 30 رطلاً والنصف الآخر يزن أقل من 30 رطلاً. هذا يعني أن 50% من الـ 200 ثعالب الماء تزن أقل من 30 رطلًا، وبالتالي 0.5 * 200 = 100 ثعالب الماء .

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول التوزيع الطبيعي:

6 أمثلة ملموسة للتوزيع الطبيعي
التوزيع الطبيعي مقابل التوزيع t: الفرق
كيفية إنشاء منحنى الجرس في إكسل
كيفية إنشاء منحنى الجرس في بايثون