توزيع ثنائي
تشرح هذه المقالة ماهية التوزيع ذي الحدين في الإحصائيات وفيم يتم استخدامه. ولذلك ستجد تعريف التوزيع ذي الحدين، وأمثلة على التوزيعات ذات الحدين وخصائص هذا النوع من التوزيع الاحتمالي. بالإضافة إلى ذلك، سوف تكون قادرًا على حساب أي احتمال للتوزيع ذي الحدين باستخدام الآلة الحاسبة عبر الإنترنت.
ما هو التوزيع ذو الحدين؟
التوزيع ذو الحدين هو توزيع احتمالي يحسب عدد النجاحات عند إجراء سلسلة من التجارب الثنائية المستقلة مع احتمال ثابت للنجاح.
بمعنى آخر، التوزيع ذو الحدين هو توزيع يصف عدد النتائج الناجحة لسلسلة من تجارب برنولي.
تذكر أن اختبار برنولي هو تجربة لها نتيجتان محتملتان: “النجاح” و”الفشل”. لذلك، إذا كان احتمال “النجاح” هو p ، فإن احتمال “الفشل” هو q=1-p .
بشكل عام، يتم تحديد العدد الإجمالي للتجارب التي تم إجراؤها باستخدام المعلمة n ، بينما p هو احتمال نجاح كل تجربة. وبالتالي، يتم كتابة المتغير العشوائي الذي يتبع التوزيع ذي الحدين على النحو التالي:
![]()
لاحظ أنه في التوزيع ذي الحدين، يتم تكرار نفس التجربة بالضبط n مرات وتكون التجارب مستقلة عن بعضها البعض، وبالتالي فإن احتمال نجاح كل تجربة هو نفسه (p) .
التوزيع ذو الحدين يمكن أن يسمى أيضًا التوزيع ذو الحدين .
أمثلة التوزيع ذي الحدين
بمجرد أن رأينا تعريف التوزيع ذي الحدين، سنرى عدة أمثلة للمتغيرات التي تتبع هذا النوع من التوزيع لفهم المفهوم بشكل أفضل.
- عدد مرات ظهور الوجه عند رمي قطعة النقود 25 مرة.
- عدد التسديدات التي ينفذها لاعب كرة السلة عندما يسدد باتجاه السلة 60 مرة من نفس الموقع.
- عدد المرات التي حصلنا فيها على الرقم 6 عن طريق رمي حجر النرد 30 مرة.
- عدد الناجحين في الامتحان من أصل 50 طالباً.
- عدد الوحدات المعيبة في عينة مكونة من 100 منتج.
صيغة التوزيع ذات الحدين
بالنظر إلى المعلمات x، n، p، يتم تعريف الدالة الاحتمالية للتوزيع ذي الحدين على أنها الرقم التوافقي لـ n في x مرات p x مرات (1-p) nx .
ولذلك، فإن صيغة حساب احتمال التوزيع ذي الحدين هي:

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب احتمال وجود متغير يتبع التوزيع ذي الحدين.
ومن ناحية أخرى، يتم حساب الاحتمال التراكمي للتوزيع ذي الحدين من خلال جمع احتمالات عدد حالات النجاح المعنية وجميع الاحتمالات السابقة. لذا، فإن صيغة حساب الاحتمال التراكمي للتوزيع ذي الحدين هي:
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e31ef4ae023b8bf51c0b6816bc787c91_l3.png)
تمرين محلول على التوزيع ذي الحدين
- ألقينا قطعة نقود 10 مرات، ما احتمال الحصول على 6 صور؟
المتغير في هذه المشكلة يتبع التوزيع ذي الحدين لأن جميع عمليات الإطلاق مستقلة عن بعضها البعض ولها أيضًا نفس احتمالية النجاح.
بشكل ملموس، احتمال النجاح هو 50٪، حيث أن نتيجة واحدة فقط من النتيجتين المحتملتين تعتبر ناجحة.
![]()
لذلك، فإن توزيع هذا التمرين هو ذو حدين بإجمالي 10 تجارب واحتمال 0.5.
![]()
لذا، لتحديد احتمال الحصول على ستة صور، علينا تطبيق صيغة التوزيع ذات الحدين.
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-17346d59c641378880b734dfe88210f6_l3.png)
لذا، فإن احتمال الحصول على ستة صور بالضبط من خلال رمي قطعة نقود عشر مرات هو 20.51%.
خصائص التوزيع ذي الحدين
التوزيع ذو الحدين له الخصائص التالية:
- يتم تعريف التوزيع ذي الحدين بمعلمتين: n هو العدد الإجمالي لتجارب برنولي، ومن ناحية أخرى، p هو احتمال نجاح كل تجربة برنولي.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cd9728a237a5f49107bf14f440620936_l3.png)
- متوسط التوزيع ذو الحدين يساوي حاصل ضرب العدد الإجمالي للتجارب مضروبًا في احتمال نجاح كل تجربة. لذلك، لحساب متوسط التوزيع ذي الحدين، يجب ضرب n في p .
![]()
- تباين التوزيع ذي الحدين يساوي إجمالي عدد المحاولات مضروبًا في احتمال النجاح واحتمال الفشل.
![]()
- صيغة دالة الاحتمال للتوزيع ذي الحدين هي كما يلي:
![]()
- وبالمثل، فإن صيغة دالة التوزيع التراكمي للتوزيع ذي الحدين هي:
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e31ef4ae023b8bf51c0b6816bc787c91_l3.png)
- مجموع توزيعين مستقلين ذوي الحدين بنفس الاحتمال يعادل توزيع ذي الحدين بنفس قيمة الاحتمال p و n هو مجموع العدد الإجمالي لمحاولات التوزيعين.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dbc1a01b2d5654864d688cc46ac3a2e6_l3.png)
![]()
- توزيع برنولي هو حالة خاصة من التوزيع ذي الحدين حيث n=1 ، أي يتم تنفيذ تجربة واحدة فقط.
![]()
- إذا كان X 1 , X 2 ,…, X k متغيرات عشوائية مستقلة من هذا القبيل
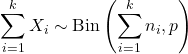
حاسبة التوزيع ذات الحدين
أدخل قيم المعلمات p وn و x للتوزيع ذي الحدين في الآلة الحاسبة التالية لحساب الاحتمال. تحتاج إلى تحديد الاحتمالية التي تريد حسابها وإدخال الأرقام باستخدام النقطة كفاصل عشري، على سبيل المثال 0.1667.