كيفية حساب الارتباط بين المتغيرات المستمرة والفئوية

عندما نريد حساب الارتباط بين متغيرين متصلين، نستخدم بشكل عام معامل ارتباط بيرسون .

ومع ذلك، عندما نريد حساب الارتباط بين متغير مستمر ومتغير قاطع ، يمكننا استخدام ما يسمى الارتباط الثنائي النقطي .

يتم استخدام الارتباط الثنائي النقطي لحساب الارتباط بين متغير فئوي ثنائي (متغير يمكن أن يأخذ قيمتين فقط) ومتغير مستمر وله الخصائص التالية:

• يمكن أن يتراوح الارتباط بين النقطة الثنائية بين -1 و1.
• لكل مجموعة تم إنشاؤها بواسطة المتغير الثنائي، من المفترض أن المتغير المستمر يتم توزيعه بشكل طبيعي بتباينات متساوية.
• لكل مجموعة تم إنشاؤها بواسطة المتغير الثنائي، من المفترض أنه لا توجد قيم متطرفة.

يوضح المثال التالي كيفية حساب الارتباط النقطي الثنائي عمليًا.

مثال: حساب الارتباط النقطي الثنائي

لنفترض أن أستاذًا جامعيًا يريد تحديد ما إذا كانت هناك علاقة بين الجنس والنتيجة في اختبار مؤهل معين.

قام بجمع البيانات التالية عن 12 ولدًا و12 فتاة في فصله:

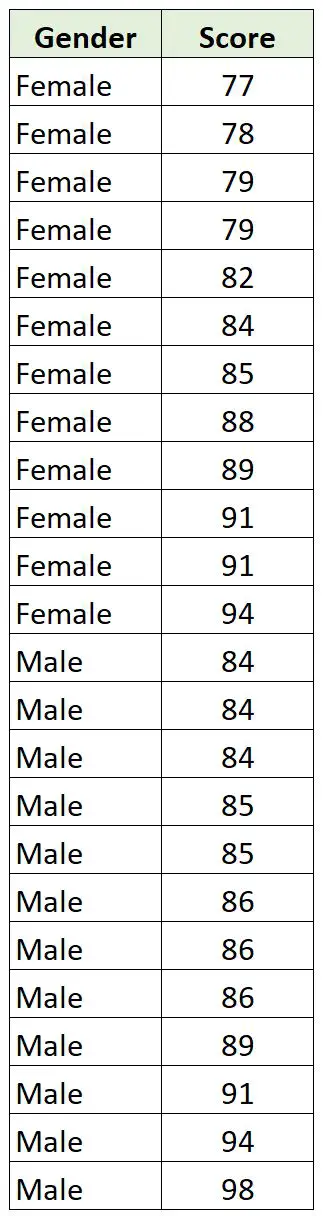
وبما أن الجنس متغير قاطع والنتيجة متغير مستمر، فمن المنطقي حساب علاقة ترابط ثنائية النقطة بين المتغيرين.

يمكن للأستاذ استخدام أي برنامج إحصائي (بما في ذلك Excel وR وPython وSPSS وStata) لحساب الارتباط الثنائي النقطة بين المتغيرين.

يوضح الكود التالي كيفية حساب الارتباط النقطي الثنائي في R، باستخدام القيمة 0 لتمثيل الإناث و1 لتمثيل الذكور لمتغير الجنس:

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

من النتيجة يمكننا أن نرى أن معامل الارتباط ثنائي النقطة هو 0.281 والقيمة p المقابلة هي 0.1833 .

وبما أن معامل الارتباط إيجابي، فإن هذا يخبرنا بوجود ارتباط إيجابي بين الجنس والنتيجة.

نظرًا لأننا قمنا بترميز الذكور بـ 1 والإناث بـ 0، فهذا يشير إلى أن الدرجات تميل إلى أن تكون أعلى بالنسبة للذكور (أي أن الدرجات تميل إلى الزيادة مع “زيادة” الجنس). » من 0 إلى 1).

ومع ذلك، بما أن القيمة p لا تقل عن 0.05، فإن معامل الارتباط هذا ليس ذا دلالة إحصائية.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية حساب الارتباط الثنائي النقطي باستخدام برامج إحصائية مختلفة:

كيفية حساب الارتباط بين النقطة والثنائي في إكسيل
كيفية حساب الارتباط النقطي الثنائي في R
كيفية حساب الارتباط النقطي الثنائي في بايثون