المثلية

تشرح هذه المقالة ماهية المثلية في الإحصائيات. لذا، ستجد تعريف المثلية الجنسية، وما هي أسباب عدم وجود المثلية في نموذج الانحدار والمزيد، وكيفية إصلاحها.

ما هي المثلية؟

التماثل هو سمة من سمات نموذج الانحدار الذي تكون أخطاء المتغيرات التوضيحية فيه تباينًا ثابتًا. أي أنه عندما يكون تباين الخطأ لنموذج الانحدار ثابتًا، فإن النموذج المذكور يُظهر التماثل، وبالتالي فهو نموذج مثلي.

تذكر أن الخطأ (أو المتبقي) يتم تعريفه على أنه الفرق بين القيمة الحقيقية والقيمة المقدرة بواسطة نموذج الانحدار.

عند تشغيل نموذج الانحدار، سنحصل على قيمة مختلفة عن التعبير السابق لكل ملاحظة. وبالتالي، فإن النموذج الإحصائي المتجانس هو النموذج الذي يكون فيه تباين الأخطاء المحسوبة ثابتًا خلال الملاحظات.

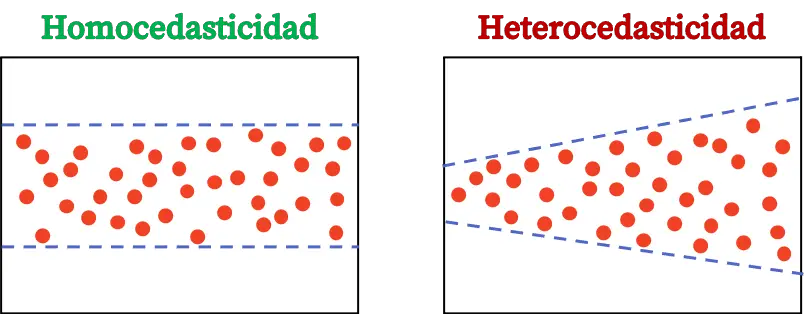
من المهم أن يُظهر نموذج الانحدار المثلية؛ في الواقع، هذا هو أحد الافتراضات السابقة لنماذج الانحدار. إذا لم تكن البقايا متجانسة، فمن الأفضل إعادة النموذج بطريقة أخرى للحصول على المتجانسة. وبخلاف ذلك، فمن المرجح أن يكون تقدير معاملات الانحدار خاطئًا، كما ستحدث أخطاء في اختبار الفرضيات عند قبول الفرضيات الصفرية التي يجب رفضها بالفعل.

أسباب عدم وجود المثلية

الأسباب الأكثر شيوعًا لعدم احتواء النموذج على المثلية هي:

• عندما يكون نطاق البيانات واسعًا جدًا مقارنة بالمتوسط. إذا كانت هناك قيم كبيرة جدًا وقيم صغيرة جدًا في نفس العينة الإحصائية، فمن المحتمل أن نموذج الانحدار الذي تم الحصول عليه ليس متجانسًا.
• يؤدي حذف المتغيرات في نموذج الانحدار أيضًا إلى نقص التجانس. ومن الناحية المنطقية، إذا لم يتم تضمين متغير ذي صلة في النموذج، فسيتم تضمين تغيره في البقايا ولن يتم إصلاحه بالضرورة.
• قد يؤدي التغيير في البنية إلى عدم ملاءمة النموذج لمجموعة البيانات، وبالتالي، فإن تباين البقايا ليس ثابتًا.
• عندما تكون لبعض المتغيرات قيم أكبر بكثير من المتغيرات التوضيحية الأخرى، فقد لا يكون للنموذج تجانس. في هذه الحالة، يمكن نسبية المتغيرات لحل المشكلة.

ومع ذلك، هناك بعض الحالات التي يصعب بطبيعتها تقديمها على أنها مثلية. على سبيل المثال، إذا قمنا بنمذجة دخل شخص ما من خلال إنفاقه على الطعام، فإن الأشخاص الأكثر ثراءً لديهم تباين أكبر بكثير في إنفاقهم على الطعام مقارنة بالأشخاص الأكثر فقراً. لأن الغني يأكل أحياناً في مطاعم غالية وأحياناً أخرى في مطاعم رخيصة، على عكس الفقير الذي يأكل دائماً في المطاعم الرخيصة. ولذلك، فمن الصعب تحقيق المثلية في نموذج الانحدار.

تصحيح البيانات لتحقيق المثلية

عندما لا يكون نموذج الانحدار الذي تم الحصول عليه متجانسًا، يمكن محاولة التصحيحات التالية لتحقيق التجانس:

• احسب اللوغاريتم الطبيعي للمتغير المستقل، وهذا مفيد بشكل عام عندما يزيد تباين البقايا في الرسم البياني.
• اعتمادًا على قطعة الأرض المتبقية، قد يكون هناك نوع آخر من تحويل المتغير المستقل أكثر عملية. على سبيل المثال، إذا كان الرسم البياني على شكل قطع مكافئ، فيمكننا حساب مربع المتغير المستقل وإضافة هذا المتغير إلى النموذج.
• يمكن أيضًا استخدام متغيرات أخرى للنموذج؛ عن طريق إزالة أو إضافة متغير، يمكن تعديل تباين البقايا.
• بدلاً من استخدام معيار المربعات الصغرى، يمكن استخدام معيار المربعات الصغرى المرجحة.

المثلية والتباين

أخيرًا، سنرى ما هو الفرق بين المثلية والتباين، حيث أنهما مفهومان إحصائيان مهمان لنماذج الانحدار.

تعد التغايرية خاصية إحصائية تشير إلى أن بقايا نموذج الانحدار لا تحتوي على تباين ثابت، وبالتالي فإن تباين الأخطاء ليس هو نفسه في جميع أنحاء المخطط.

الفرق بين المثلية والتغايرية هو ثبات تباين الخطأ. تشير التماثلية إلى أن تباين الخطأ ثابت، بينما تشير التباينية إلى أن تباين الخطأ ليس ثابتًا.