تحليل التباين أحادي الاتجاه أو ثنائي الاتجاه: متى يتم استخدامه؟

يتم استخدام تحليل التباين (ANOVA) ، وهو اختصار لعبارة “تحليل التباين”، لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

النوعان الأكثر شيوعًا من ANOVA هما ANOVA أحادي الاتجاه وANOVA ثنائي الاتجاه.

تحليل التباين أحادي الاتجاه: يستخدم لتحديد كيفية تأثير العامل على متغير الاستجابة.

تحليل التباين ثنائي الاتجاه: يستخدم لتحديد كيفية تأثير عاملين على متغير الاستجابة ولتحديد ما إذا كان هناك تفاعل بين العاملين على متغير الاستجابة أم لا.

توفر الأمثلة التالية مثالاً لكيفية تنفيذ كل نوع من أنواع ANOVA.

مثال: تحليل التباين أحادي الاتجاه

لنفترض أن الأستاذ يريد معرفة ما إذا كانت ثلاث تقنيات دراسة مختلفة تؤدي إلى درجات اختبار مختلفة. ولاختبار ذلك، قام بتجنيد 30 طالبًا للمشاركة في دراسة وطلب من كل واحد منهم بشكل عشوائي استخدام إحدى التقنيات الثلاثة للتحضير للامتحان. وبعد شهر، يأخذ جميع الطلاب نفس الاختبار.

تظهر أدناه نتائج اختبار كل طالب:

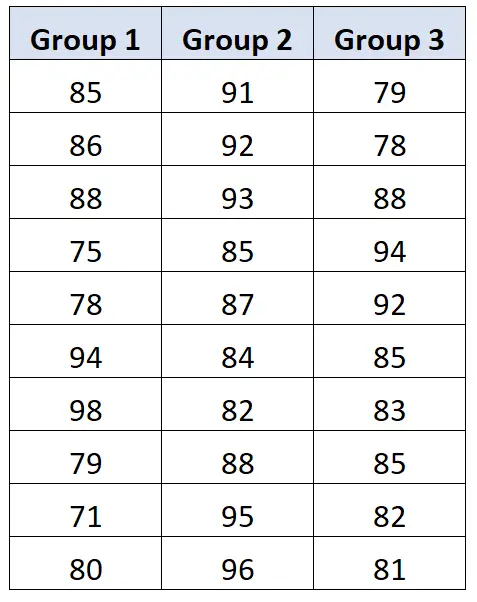
يقوم الأستاذ بإجراء تحليل التباين أحادي الاتجاه ويحصل على النتائج التالية:

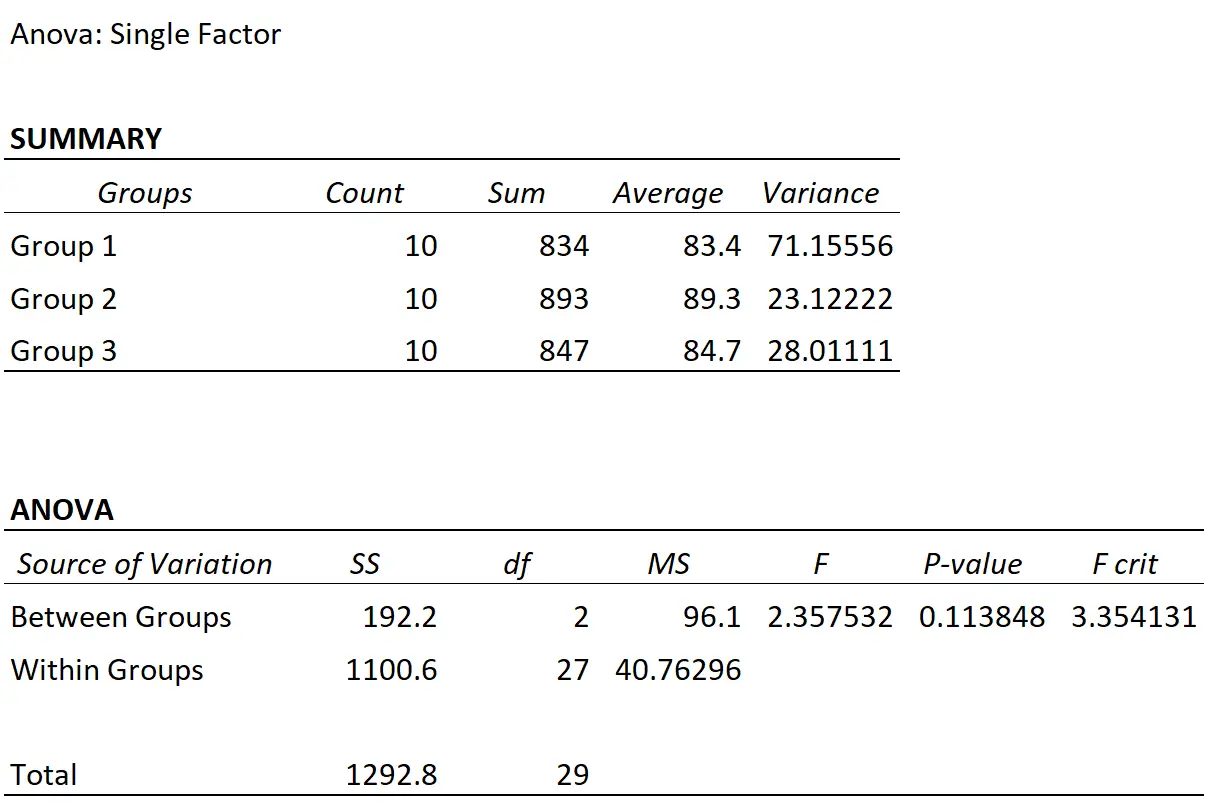
إحصائيات اختبار F هي 2.3575 والقيمة p المقابلة هي 0.1138 . وبما أن هذه القيمة الاحتمالية لا تقل عن 0.05، فليس لدينا أدلة كافية للقول بأن تقنيات الدراسة الثلاثة تؤدي إلى متوسط درجات مختلفة في الامتحانات.

مثال: تحليل التباين ثنائي الاتجاه

لنفترض أن عالم النبات يريد معرفة ما إذا كان نمو النبات يتأثر بالتعرض لأشعة الشمس وتكرار الري. تزرع 40 بذرة وتتركها تنمو لمدة شهرين في ظروف مختلفة من التعرض لأشعة الشمس وتكرار الري. وبعد شهرين، تسجل ارتفاع كل نبات. النتائج موضحة أدناه:

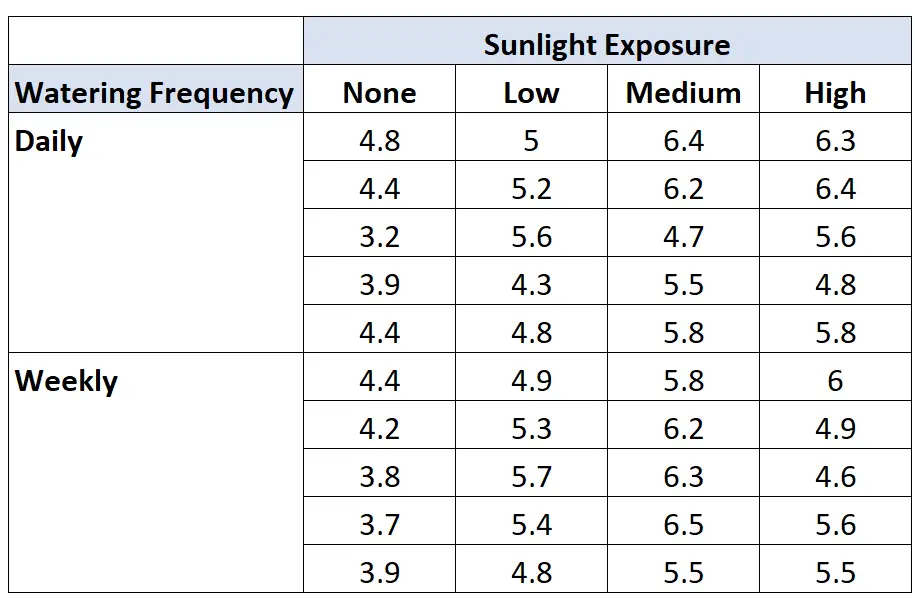
يقوم الأستاذ بإجراء تحليل التباين ثنائي الاتجاه ويحصل على النتائج التالية:

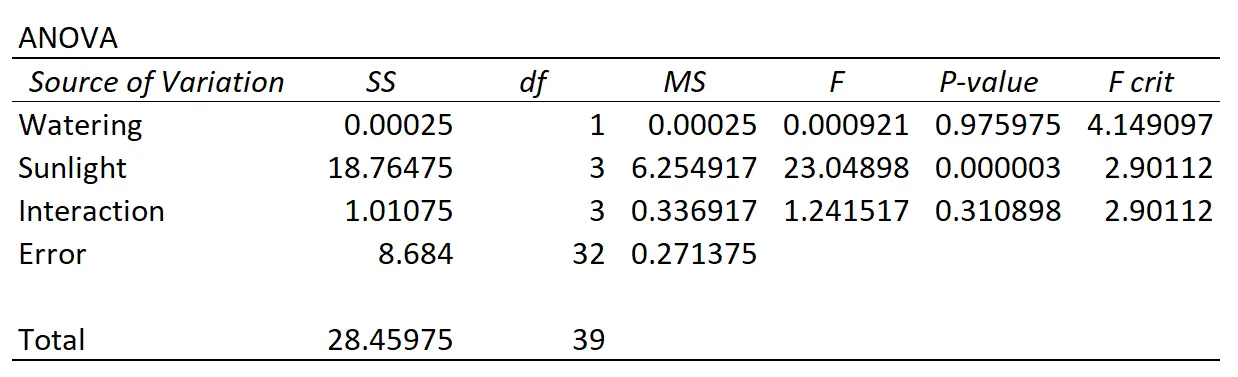
وإليك كيفية تفسير النتائج:

• وكانت القيمة p للتفاعل بين تكرار الري والتعرض للشمس 0.310898 . وهذا ليس ذو دلالة إحصائية عند مستوى 0.05 ألفا.
• وكانت القيمة p لتكرار الري 0.975975 . وهذا ليس ذو دلالة إحصائية عند مستوى 0.05 ألفا.
• وكانت القيمة p للتعرض لأشعة الشمس 0.000003 . وهذا ذو دلالة إحصائية عند مستوى ألفا 0.05.

تشير هذه النتائج إلى أن التعرض لأشعة الشمس هو العامل الوحيد الذي له تأثير ذو دلالة إحصائية على ارتفاع النبات.

وبما أنه لا يوجد أي تأثير تفاعلي، فإن تأثير التعرض لأشعة الشمس يكون ثابتًا عند كل مستوى من مستويات تكرار الري. ببساطة، ما إذا كان يتم ري النبات يوميًا أو أسبوعيًا ليس له أي تأثير على كيفية تأثير التعرض لأشعة الشمس على النبات.

عملي: ما هو تحليل التباين (ANOVA) الذي يجب عليك استخدامه؟

استخدم المسائل التدريبية التالية لفهم متى يجب عليك استخدام ANOVA أحادي الاتجاه أو ثنائي الاتجاه بشكل أفضل.

المشكلة رقم 1: الزراعة

يريد أحد المزارعين معرفة ما إذا كانت ثلاثة أنواع مختلفة من الأسمدة تؤدي إلى عوائد مختلفة. ولاختبار ذلك، قام بنشر كل نوع من الأسمدة في 10 حقول مختلفة وقياس إجمالي العائد في نهاية موسم النمو.

ما نوع تحليل التباين (ANOVA) الذي ينبغي عليه استخدامه لتحديد ما إذا كانت الأسمدة المختلفة تؤدي إلى إنتاجية محاصيل مختلفة؟

الإجابة: يجب عليه استخدام تحليل التباين أحادي الاتجاه لأنه ينظر إلى عامل واحد فقط: الأسمدة. يمكن أن يخبره تحليل التباين الأحادي الاتجاه ما إذا كان هناك فرق ذو دلالة إحصائية في إنتاجية المحاصيل بين الأنواع الثلاثة المختلفة للأسمدة أم لا.

المشكلة رقم 2: علم الأحياء

يريد عالم الأحياء أن يعرف مدى تأثير مستويات التربة المختلفة (منخفضة ومتوسطة وعالية) وتكرار الري (أسبوعيًا وشهريًا) على نمو نبات معين.

ما نوع تحليل التباين (ANOVA) الذي ينبغي استخدامه لتحديد ما إذا كانت مجموعات مختلفة من التعرض لأشعة الشمس وتكرار الري تؤدي إلى مستويات مختلفة من نمو النبات؟

الإجابة: يجب عليها استخدام تحليل التباين ثنائي الاتجاه لأنها تنظر إلى عاملين: التعرض لأشعة الشمس وتكرار الري. يمكن لـ ANOVA ثنائي الاتجاه معرفة ما إذا كانت المستويات المختلفة لكل عامل تؤثر على نمو النبات بشكل مختلف وما إذا كان هناك تأثير تفاعل بين ضوء الشمس وتكرار الري على نمو النبات أم لا.

المشكلة رقم 3: الأدوية

يريد أحد الباحثين الطبيين معرفة ما إذا كانت أربعة أدوية مختلفة تسبب انخفاضات مختلفة في متوسط ضغط الدم لدى المرضى. تم تعيين 20 مريضًا عشوائيًا لاستخدام كل دواء لمدة شهر، ثم قياس الانخفاض في ضغط الدم لدى كل مريض.

ما نوع تحليل التباين (ANOVA) الذي ينبغي استخدامه لتحديد ما إذا كانت الأدوية الأربعة المختلفة لها تأثيرات مختلفة على خفض ضغط الدم؟

الجواب: يجب عليه استخدام تحليل التباين الأحادي لأنه ينظر إلى عامل واحد فقط: نوع الدواء. يمكن لـ ANOVA أحادي الاتجاه أن يخبره ما إذا كان هناك فرق ذو دلالة إحصائية في متوسط انخفاض ضغط الدم بين الأنواع الأربعة من الأدوية أم لا.

مصادر إضافية

استخدم البرامج التعليمية التالية لفهم تحليل التباين أحادي الاتجاه بشكل أفضل:

• مقدمة إلى تحليل التباين الأحادي (One-Way ANOVA).
• كيفية إجراء ANOVA أحادي الاتجاه في Excel
• كيفية إجراء ANOVA أحادي الاتجاه في R

واستخدم هذه البرامج التعليمية لفهم تحليل التباين ثنائي الاتجاه بشكل أفضل:

• مقدمة إلى تحليل التباين ثنائي الاتجاه
• كيفية إجراء ANOVA ثنائي الاتجاه في Excel
• كيفية إجراء ANOVA ثنائي الاتجاه في R