أنواع عدم التماثل

ستتعرف في هذه المقالة على عدد أنواع عدم التماثل الموجودة في الإحصائيات. وبالتالي، يتم شرح كل نوع من عدم التماثل بالأمثلة، وبالإضافة إلى ذلك، ستتمكن من رؤية كيفية حساب عدم التماثل في التوزيع.

ما هي أنواع عدم التماثل؟

في الإحصاء، هناك ثلاثة أنواع من عدم التماثل :

• الانحراف الإيجابي : يحتوي التوزيع على قيم مختلفة على يمين الوسط أكثر من اليسار.
• الانحراف السلبي : يحتوي التوزيع على قيم مختلفة على يسار الوسط أكثر من قيمه على يمينه.
• التناظر : التوزيع له نفس عدد القيم على يسار ويمين المتوسط.

يتم شرح كل نوع من عدم التماثل بمزيد من التفاصيل أدناه.

عدم التماثل الإيجابي

عندما يكون للتوزيع انحراف إيجابي ، فهذا يعني أن الرسم البياني له الذيل الأيمن أطول من الذيل الأيسر. أي أن التوزيع له قيم مختلفة أكثر على يمين المتوسط.

المنحنى في المثال السابق غير متماثل بشكل إيجابي لأن هناك قيمًا أكثر بكثير على يمين المتوسط منها على يساره. كما ترون من الرسم البياني، فإن الشريط الموضح باللون الأخضر أكبر بكثير من الشريط البرتقالي.

عدم التماثل السلبي

في الإحصائيات، يُقال إن التوزيع لديه انحراف سلبي عندما يكون للرسم البياني الخاص به الذيل الأيسر أطول من الذيل الأيمن. أي أن التوزيع المنحرف سلبًا يعني أنه يحتوي على قيم أكثر اختلافًا على يسار الوسط.

إذا نظرت إلى الرسم البياني السابق، فستجد أن هناك قيمًا على يسار المتوسط أكثر من القيم على اليمين، وبالتالي فإن المنحنى منحرف بشكل سلبي.

تناظر

يكون التوزيع متماثلًا عندما يكون عدد القيم الموجودة على يسار المتوسط مساويًا لعدد القيم الموجودة على يمين المتوسط. وبالتالي فإن المتوسط يعمل كمحور التماثل.

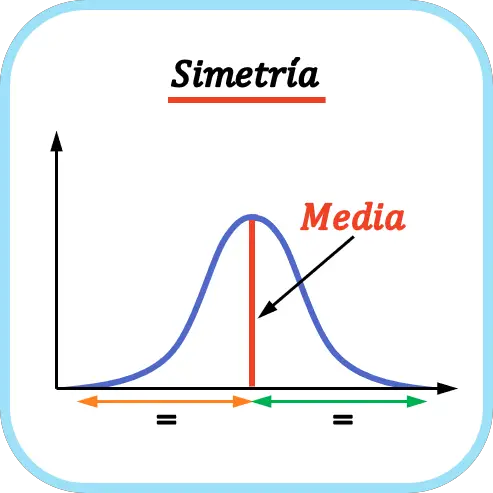
كما هو موضح في المثال أعلاه، فإن عدد القيم الموجودة على يسار متوسط التوزيع الاحتمالي الممثل يتطابق مع عدد القيم الموجودة على يمين المتوسط، لذلك فهو توزيع متماثل.

كيفية تحديد نوع عدم التماثل

الآن بعد أن عرفنا ما هي أنواع عدم التماثل المختلفة في الإحصائيات، دعونا نرى كيفية معرفة نوع عدم التماثل الذي يتوافق معه التوزيع الاحتمالي.

تقليديًا، يتم توضيح أنه يمكننا معرفة نوع انحراف التوزيع بناءً على العلاقة بين متوسطه ووسيطه (سواء كان أكبر أو مكافئًا أو أصغر). ومع ذلك، هذه الخاصية ليست دائما راضية. وبالتالي، لتحديد انحراف التوزيع، يجب حساب معامل الانحراف فيشر.

يتم حساب معامل عدم تناسق فيشر باستخدام الصيغة التالية:

أو ما يعادلها:

ذهب

هو التوقع الرياضي

الوسط الحسابي و

الانحراف المعياري .

وبمجرد حساب معامل فيشر، فإن علامته تجعل من الممكن تحديد نوع عدم التماثل الذي يمثله التوزيع:

• إذا كان معامل انحراف فيشر موجبًا، يكون التوزيع منحرفًا بشكل إيجابي.
• إذا كان معامل انحراف فيشر سالبًا، يكون التوزيع منحرفًا سلبيًا.
• إذا كان التوزيع متماثلًا، فإن معامل التواء فيشر يساوي الصفر (والعكس ليس صحيحًا دائمًا).