Anova في اتجاه واحد والتدابير المتكررة anova: الفرق

هناك نوعان من نماذج ANOVA التي غالبًا ما يخلط الطلاب بينهما هما ANOVA أحادي الاتجاه ومقاييس ANOVA المتكررة أحادية الاتجاه.

وهنا الفرق البسيط:

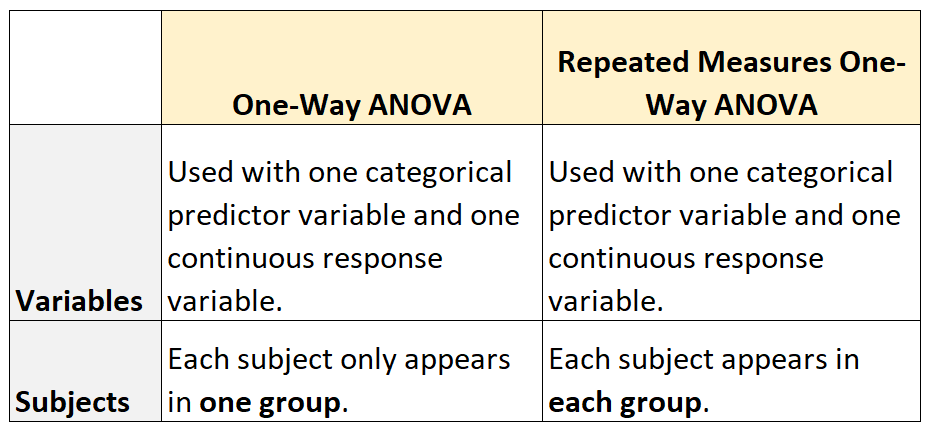
يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

يتم استخدام المقاييس المتكررة أحادية الاتجاه ANOVA لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات أو أكثر تظهر فيها نفس المواضيع في كل مجموعة أم لا .

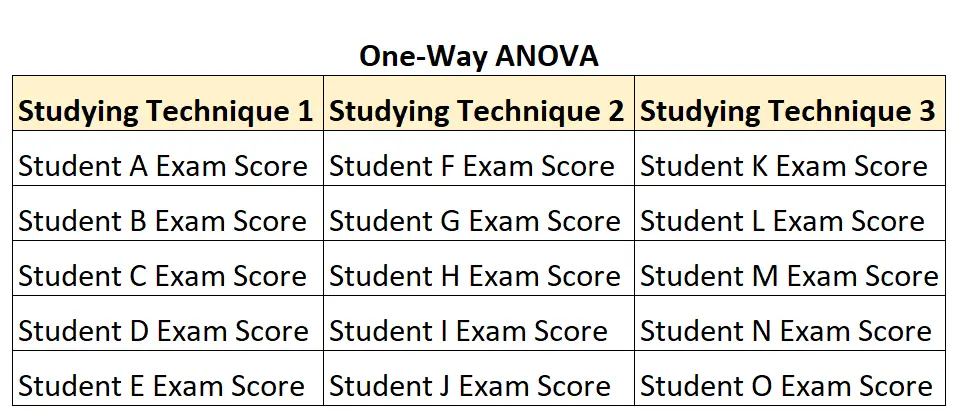
على سبيل المثال، لنفترض أن الأستاذ يريد تحديد ما إذا كانت ثلاث تقنيات دراسة مختلفة تؤدي إلى متوسط درجات مختلف في الامتحانات. ولاختبار ذلك، قام بتجنيد 15 طالبًا وتخصيص 5 طلاب بشكل عشوائي لاستخدام كل أسلوب من أساليب الدراسة لمدة أسبوع قبل الامتحان.

يمكنه استخدام تحليل التباين (ANOVA) أحادي الاتجاه لاختبار الاختلافات بين متوسطات المجموعة، نظرًا لأن كل طالب يظهر فقط في مجموعة واحدة فقط.

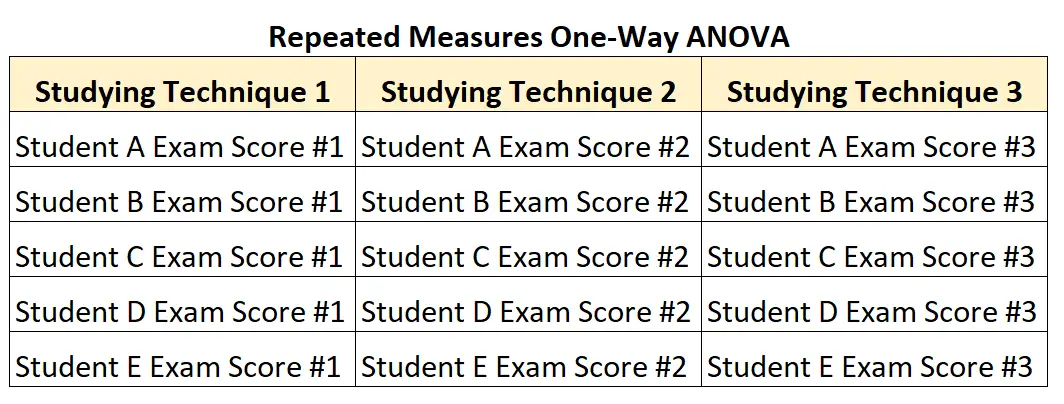
ومع ذلك، لنفترض أن الأستاذ قام بتجنيد 5 طلاب فقط وطلب من كل طالب استخدام كل أسلوب دراسة لمدة ثلاثة أسابيع مختلفة للتحضير للاختبارات ذات الصعوبة المتساوية.

في هذا السيناريو، يمكنه استخدام تحليل التباين (ANOVA) المتكرر أحادي الاتجاه لاختبار متوسطات الاختلافات بين المجموعات حيث يظهر كل طالب في كل مجموعة.

متى يتم استخدام التدابير المتكررة ANOVA

يتم استخدام التدابير المتكررة ANOVA في حالتين محددتين:

1. قم بقياس متوسط درجات الأشخاص عبر ثلاث نقاط زمنية أو أكثر. على سبيل المثال، قد ترغب في قياس معدل ضربات القلب أثناء الراحة قبل شهر واحد من بدء برنامج تدريبي، ومرة واحدة في منتصف البرنامج، وشهر واحد بعد البرنامج لمعرفة ما إذا كان هناك اختلاف كبير في متوسط معدل ضربات القلب أثناء الراحة. من خلال هذه اللحظات الثلاث.

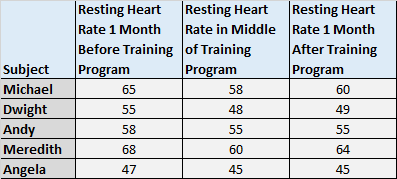
نظرًا لأنه يتم قياس معدل ضربات قلب كل شخص عدة مرات ، يمكننا استخدام تحليل التباين (ANOVA) المتكرر لتحديد ما إذا كان هناك اختلاف كبير في متوسط معدل ضربات القلب عبر هذه الفترات الزمنية الثلاث.

2. قم بقياس متوسط درجات المواد في ثلاث حالات مختلفة. على سبيل المثال، قد تطلب من المشاركين مشاهدة ثلاثة أفلام مختلفة وتقييم كل منها بناءً على مدى إعجابهم بها.

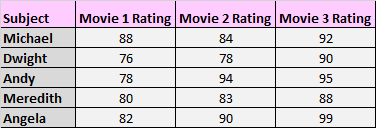
مرة أخرى، تظهر نفس المواضيع في كل مجموعة، لذلك نحتاج إلى استخدام مقاييس ANOVA المتكررة لاختبار الفرق في المتوسطات بين هذه الحالات الثلاثة.

مزايا وعيوب التدابير المتكررة ANOVA

توفر المقاييس المتكررة أحادية الاتجاه ANOVA المزايا التالية مقارنة بـ ANOVA العادية أحادية الاتجاه:

1. من الأسرع والأكثر فعالية من حيث التكلفة تعيين عدد صغير من الأفراد للمشاركة في تحليل التباين (ANOVA) للتدابير المتكررة في اتجاه واحد لأن الباحثين يمكنهم ببساطة الحصول على البيانات من نفس الأفراد عدة مرات.

2. يمكن للباحثين أن ينسبوا بعض التباين في البيانات إلى الأفراد أنفسهم، مما يسهل اكتشاف الاختلافات الحقيقية الموجودة بين المعالجات المختلفة.

ومع ذلك، فإن التدابير المتكررة أحادية الاتجاه ANOVA لها العيوب التالية:

1. إذا انسحب أحد الأفراد من التجربة، يفقد الباحثون المزيد من البيانات مقارنة بتحليل التباين العادي أحادي الاتجاه.

2. من الممكن أن يعاني الأفراد من تأثيرات الترتيب ، أي اختلافات في سلوك المشاركين بسبب الترتيب الذي تقدم به العلاجات لهم. على سبيل المثال، قد يصبح الأفراد متعبين أو متعبين بحلول الوقت الذي يخضعون فيه للعلاج الأخير.

مصادر إضافية

مقدمة إلى تحليل التباين الأحادي (One-Way ANOVA).
آلة حاسبة ANOVA أحادية الاتجاه
مقدمة للتدابير المتكررة ANOVA
حاسبة ANOVA للتدابير المتكررة في اتجاه واحد