ما أهمية المتوسط في الإحصاء؟

يمثل متوسط مجموعة البيانات متوسط قيمة مجموعة البيانات. يتم حسابه على النحو التالي:

المتوسط = Σx _ط / ن

ذهب:

• Σ: رمز يعني “المجموع”
• _xi : ^{الملاحظة} i في مجموعة بيانات
• n: إجمالي عدد الملاحظات في مجموعة البيانات

على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية مع 11 ملاحظة:

مجموعة البيانات: 3، 4، 4، 6، 7، 8، 12، 13، 15، 16، 17

يتم حساب متوسط مجموعة البيانات على النحو التالي:

المتوسط = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9.54

في الإحصاء، المتوسط مهم للأسباب التالية:

1. يعطينا المتوسط فكرة عن مكان “مركز” مجموعة البيانات.

2. بسبب طريقة حسابه، يحتوي المتوسط على معلومات من كل ملاحظة في مجموعة البيانات.

ويوضح المثال التالي هذين السببين.

مثال: احسب متوسط مجموعة من البيانات

لنفترض أن لدينا مجموعة بيانات تحتوي على أسعار مبيعات 10000 منزل مختلف في مدينة معينة.

بدلاً من النظر إلى آلاف صفوف البيانات الأولية ، يمكننا حساب متوسط القيمة لفهم متوسط سعر مبيعات المنازل في تلك المدينة بسرعة.

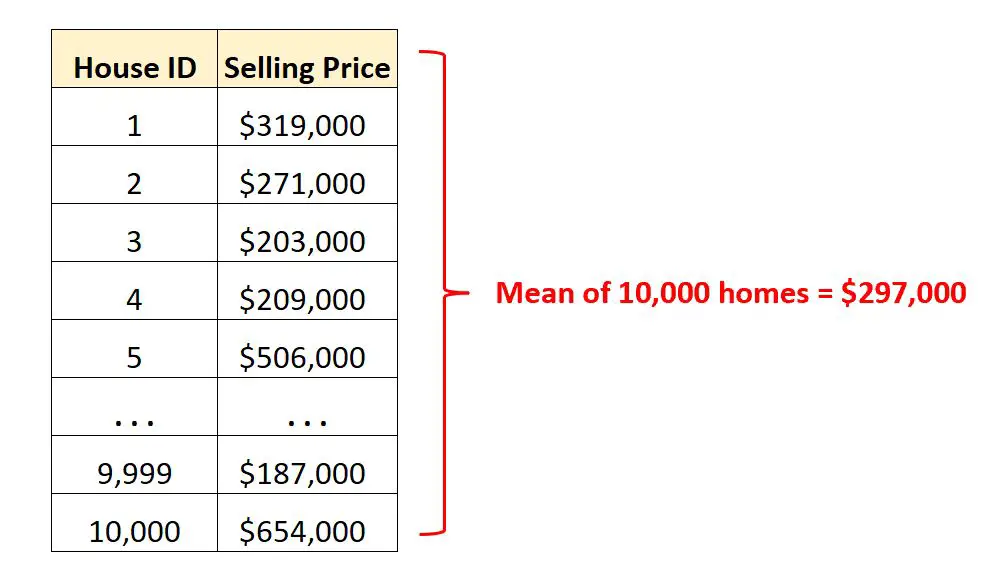
ومعرفة أن متوسط سعر البيع هو 297 ألف دولار، يعطينا فكرة عن سعر بيع المنزل “النموذجي” في هذه المدينة.

يعد تفسير هذه القيمة الفردية للمتوسط أسهل بكثير من النظر إلى جميع صفوف البيانات الأولية.

وبما أنه تم استخدام سعر بيع كل منزل لحساب المتوسط، فيمكننا ضرب متوسط سعر البيع في إجمالي عدد المنازل للعثور على إجمالي سعر البيع لجميع المنازل في تلك المدينة:

• إجمالي سعر البيع لجميع المنازل = متوسط سعر البيع * عدد المنازل
• إجمالي سعر البيع لجميع المنازل = 297.000 دولار * 10.000
• إجمالي سعر البيع لجميع المنازل = 2,970,000,000 دولار

يمكننا أن نرى أن إجمالي سعر البيع لجميع المنازل في هذه المدينة هو 2.97 مليار دولار.

متى يستخدم المتوسط

عند تحليل مجموعات البيانات، غالبًا ما نريد أن نفهم أين تكمن القيمة المركزية.

في الإحصائيات، هناك مقياسان شائعان نستخدمهما لقياس مركز مجموعة البيانات:

• المتوسط : القيمة المتوسطة في مجموعة من البيانات
• الوسيط : القيمة المتوسطة في مجموعة البيانات

المتوسط هو الطريقة الأكثر شيوعًا لقياس مركز مجموعة البيانات، ولكنه قد يكون مضللاً في المواقف التالية:

• عندما يكون التوزيع غير متماثل .
• عندما يحتوي التوزيع على القيم المتطرفة .

لتوضيح ذلك، خذ بعين الاعتبار المثالين التاليين.

مثال 1: حساب متوسط التوزيع المنحرف

خذ بعين الاعتبار التوزيع التالي للرواتب لسكان مدينة معينة:

الأجور المرتفعة على الجانب الأيمن من التوزيع تدفع المتوسط بعيدا عن مركز التوزيع.

وبالتالي فإن المتوسط يعكس الراتب “النموذجي” الذي يتقاضاه المقيم بشكل أفضل من المتوسط، لأن التوزيع منحرف نحو اليمين.

في هذا المثال بالذات، يبلغ متوسط الراتب 47000 دولار بينما يبلغ متوسط الراتب 32000 دولار.

وبالتالي، فإن الوسيط يمثل أكثر بكثير الراتب النموذجي في تلك المدينة.

مثال 2: حساب المتوسط في وجود القيم المتطرفة

خذ بعين الاعتبار الرسم البياني التالي الذي يوضح المساحة المربعة للمنازل في شارع معين:

ويتأثر المتوسط بشدة بعدد قليل من المنازل الكبيرة للغاية، في حين أن المتوسط لا يتأثر.

يمكننا أن نرى أن الوسيط يقوم بعمل أفضل في التقاط اللقطات المربعة “النموذجية” لمنزل في ذلك الشارع من المتوسط، لأنه لا يتأثر بالقيم المتطرفة.

ملخص

فيما يلي ملخص موجز لأهم الوجبات السريعة من هذه المقالة:

• يمثل المتوسط القيمة المتوسطة في مجموعة من البيانات.
• المتوسط مهم لأنه يعطينا فكرة عن مكان وجود القيمة المركزية في مجموعة البيانات.
• المتوسط مهم أيضًا لأنه يحتوي على معلومات من كل ملاحظة في مجموعة البيانات.
• يمكن أن يكون المتوسط مضللاً عندما تكون مجموعة البيانات منحرفة أو تحتوي على قيم متطرفة. في هذه السيناريوهات، يعطي الوسيط فكرة أكثر دقة عن مكان “مركز” مجموعة البيانات.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول الإحصائيات الوصفية الأخرى:

لماذا يعتبر الوسيط مهم في الإحصاء؟
ما أهمية الانحراف المعياري في الإحصاء؟
متى يتم استخدام المتوسط مقابل الوسيط