كيفية إجراء الانحدار التربيعي في ستاتا

عندما يكون بين متغيرين علاقة خطية، يمكنك غالبًا استخدام الانحدار الخطي البسيط لتحديد العلاقة بينهما.

ومع ذلك، عندما يكون بين متغيرين علاقة تربيعية، يمكنك استخدام الانحدار التربيعي لتحديد العلاقة بينهما.

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار التربيعي في Stata.

مثال: الانحدار التربيعي في ستاتا

لنفترض أننا نريد أن نفهم العلاقة بين عدد ساعات العمل والسعادة. لدينا البيانات التالية عن عدد ساعات العمل أسبوعيًا ومستوى السعادة المُبلغ عنه (على مقياس من 0 إلى 100) لـ 16 شخصًا مختلفًا:

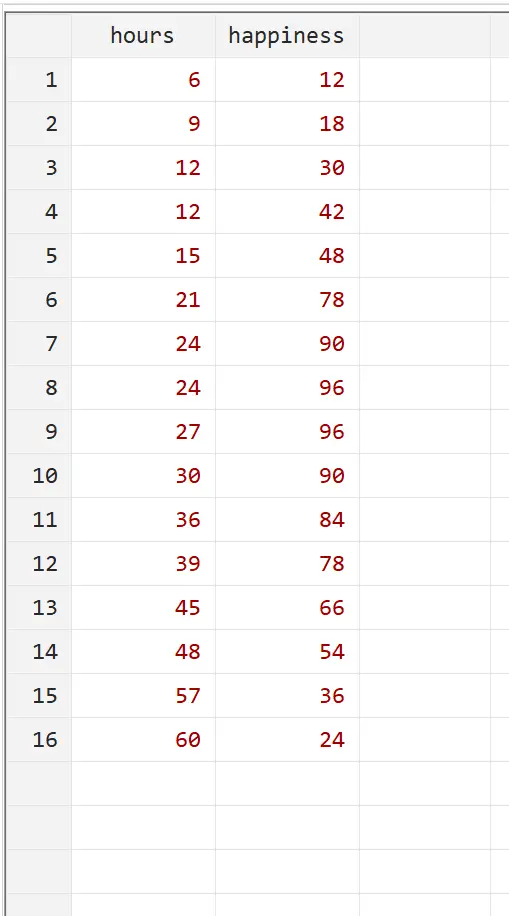
يمكنك إعادة إنتاج هذا المثال عن طريق إدخال هذه البيانات الدقيقة في Stata باستخدام البيانات > محرر البيانات > محرر البيانات (تحرير) في القائمة العلوية.

استخدم الخطوات التالية لإجراء الانحدار التربيعي في Stata.

الخطوة 1: تصور البيانات.

قبل أن نتمكن من استخدام الانحدار التربيعي، يجب أن نتأكد من أن العلاقة بين المتغير التوضيحي (الساعات) ومتغير الاستجابة (السعادة) هي بالفعل علاقة تربيعية. لذلك دعونا نتصور البيانات باستخدام مخطط التشتت عن طريق كتابة ما يلي في مربع الأوامر:

تفريق ساعات السعادة

وينتج عن ذلك المخطط المبعثر التالي:

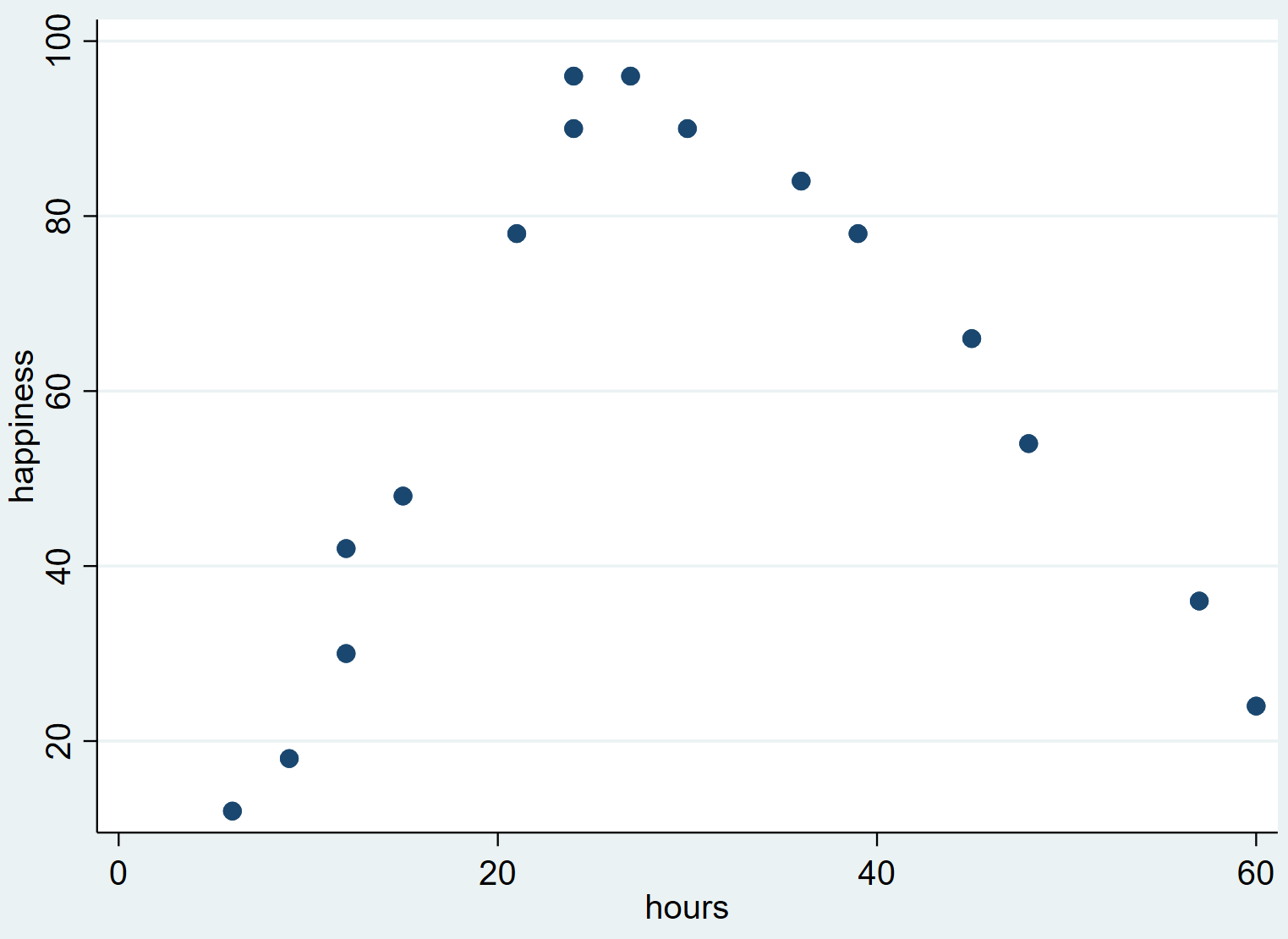
يمكننا أن نرى أن السعادة تميل إلى الزيادة مع زيادة عدد ساعات العمل من الصفر إلى نقطة معينة، ولكنها تبدأ بعد ذلك في الانخفاض عندما يتجاوز عدد ساعات العمل حوالي 30.

يشير هذا الشكل المقلوب “U” في مخطط التشتت إلى وجود علاقة تربيعية بين ساعات العمل والسعادة، مما يعني أننا يجب أن نستخدم الانحدار التربيعي لتحديد هذه العلاقة.

الخطوة 2: تنفيذ الانحدار التربيعي.

قبل ملاءمة نموذج الانحدار التربيعي للبيانات، نحتاج إلى إنشاء متغير جديد للقيم التربيعية لمتغير توقع الساعات الخاص بنا. يمكننا القيام بذلك عن طريق كتابة ما يلي في مربع الأوامر:

ساعات الجيل 2 = ساعات * ساعات

يمكننا عرض هذا المتغير الجديد بالانتقال إلى Data > Data Editor > Data Editor (Browse) من القائمة العلوية.

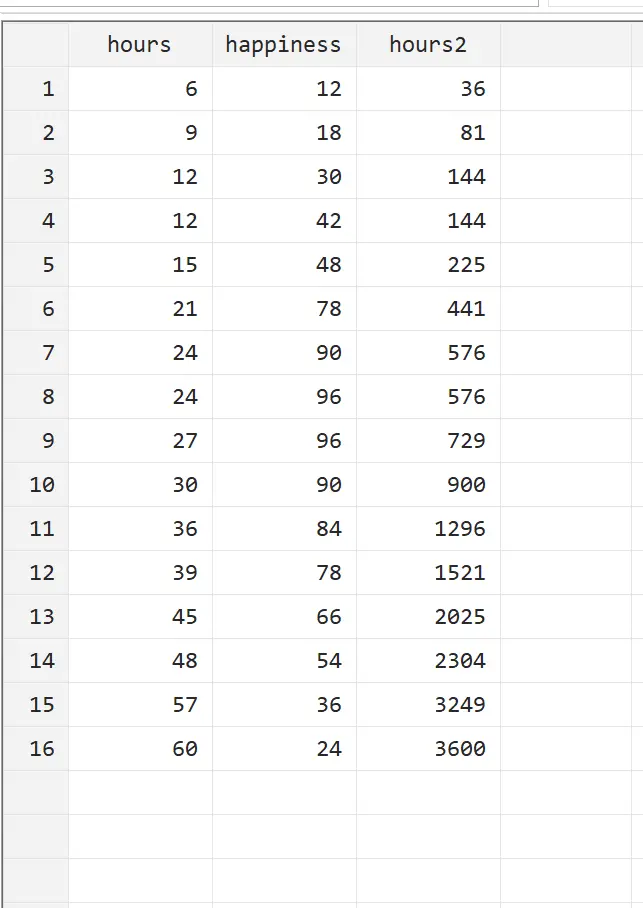
يمكننا أن نرى أنhours2 هي ببساطة ساعات مربعة. يمكننا الآن إجراء الانحدار التربيعي باستخدام الساعات والساعات2 كمتغيرات توضيحية والسعادة كمتغير الاستجابة. لإجراء انحدار تربيعي، اكتب ما يلي في مربع الأوامر:

ساعات التراجع من ساعات السعادة2

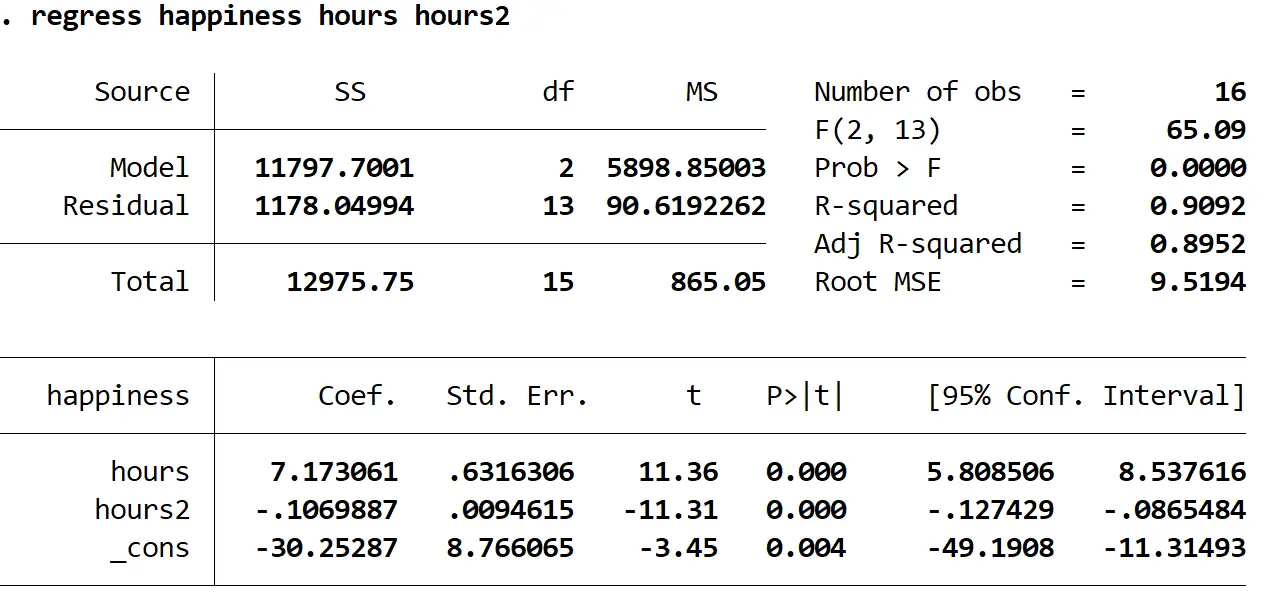
إليك كيفية تفسير الأرقام الأكثر إثارة للاهتمام في النتيجة:

غالب > و: 0.000. هذه هي القيمة p للانحدار الشامل. وبما أن هذه القيمة أقل من 0.05 فهذا يعني أن المتغيرات المتنبئة ساعات وساعات ² مجتمعة لها علاقة ذات دلالة إحصائية مع متغير الاستجابة السعادة .

ص تربيع: 0.9092. وهي نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بالمتغير التوضيحي. في هذا المثال، يمكن تفسير 90.92% من التباين في السعادة بالساعات والساعات ² .

معادلة الانحدار: يمكننا تكوين معادلة انحدار باستخدام قيم المعاملات الموضحة في جدول المخرجات. وفي هذه الحالة ستكون المعادلة:

السعادة المتوقعة = -30.25287 + 7.173061 (ساعة) – 0.1069887 ( ^ساعتان )

يمكننا استخدام هذه المعادلة للعثور على السعادة المتوقعة للفرد، بالنظر إلى عدد الساعات التي يعملها في الأسبوع.

على سبيل المثال، الشخص الذي يعمل 60 ساعة في الأسبوع يجب أن يكون مستوى سعادته 14.97:

السعادة المتوقعة = -30.25287 + 7.173061(60) – .1069887(60 ² ) = 14.97 .

وعلى العكس من ذلك، فإن الشخص الذي يعمل 30 ساعة أسبوعيًا يجب أن يكون مستوى سعادته 88.65:

السعادة المتوقعة = -30.25287 + 7.173061(30) – .1069887(30 ² ) = 88.65 .

الخطوة 3: الإبلاغ عن النتائج.

وأخيرًا، نريد الإبلاغ عن نتائج الانحدار التربيعي. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء الانحدار التربيعي لتحديد العلاقة بين عدد الساعات التي عمل فيها الفرد ومستوى سعادته المقابل (يقاس من 0 إلى 100). تم استخدام عينة مكونة من 16 شخصًا في التحليل.

وأظهرت النتائج وجود علاقة ذات دلالة إحصائية بين المتغيرات التفسيرية ساعات وساعات ² ومتغير الاستجابة السعادة (F(2, 13) = 65.09, p <0.0001).

يمثل هذان المتغيران التوضيحيان معًا 90.92% من التباين الموضح في السعادة.

وتبين أن معادلة الانحدار هي:

السعادة المتوقعة = -30.25287 + 7.173061 (ساعة) – 0.1069887 ( ^ساعتان )