كيفية استخدام الأخطاء القياسية القوية في الانحدار في ستاتا

الانحدار الخطي المتعدد هو طريقة يمكننا استخدامها لفهم العلاقة بين المتغيرات التوضيحية المتعددة ومتغير الاستجابة.

لسوء الحظ، هناك مشكلة تحدث غالبًا في الانحدار تُعرف باسم التغايرية ، حيث يوجد تغيير منهجي في تباين القيم المتبقية على نطاق من القيم المقاسة.

ويؤدي ذلك إلى زيادة التباين في تقديرات معامل الانحدار، ولكن نموذج الانحدار لا يأخذ ذلك في الاعتبار. وهذا يزيد من احتمالية أن يدعي نموذج الانحدار أن المصطلح الموجود في النموذج له دلالة إحصائية، في حين أنه ليس كذلك في الواقع.

إحدى الطرق لحساب هذه المشكلة هي استخدام الأخطاء المعيارية القوية ، والتي تكون أكثر “قوة” لمشكلة التغايرية وتميل إلى توفير قياس أكثر دقة للخطأ المعياري الحقيقي لمعامل الانحدار.

يشرح هذا البرنامج التعليمي كيفية استخدام الأخطاء القياسية القوية في تحليل الانحدار في Stata.

مثال: أخطاء قياسية قوية في Stata

سوف نستخدم مجموعة بيانات Stata المدمجة تلقائيًا لتوضيح كيفية استخدام الأخطاء القياسية القوية في الانحدار.

الخطوة 1: تحميل وعرض البيانات.

أولاً، استخدم الأمر التالي لتحميل البيانات:

الاستخدام التلقائي للنظام

ثم قم بعرض البيانات الأولية باستخدام الأمر التالي:

ر

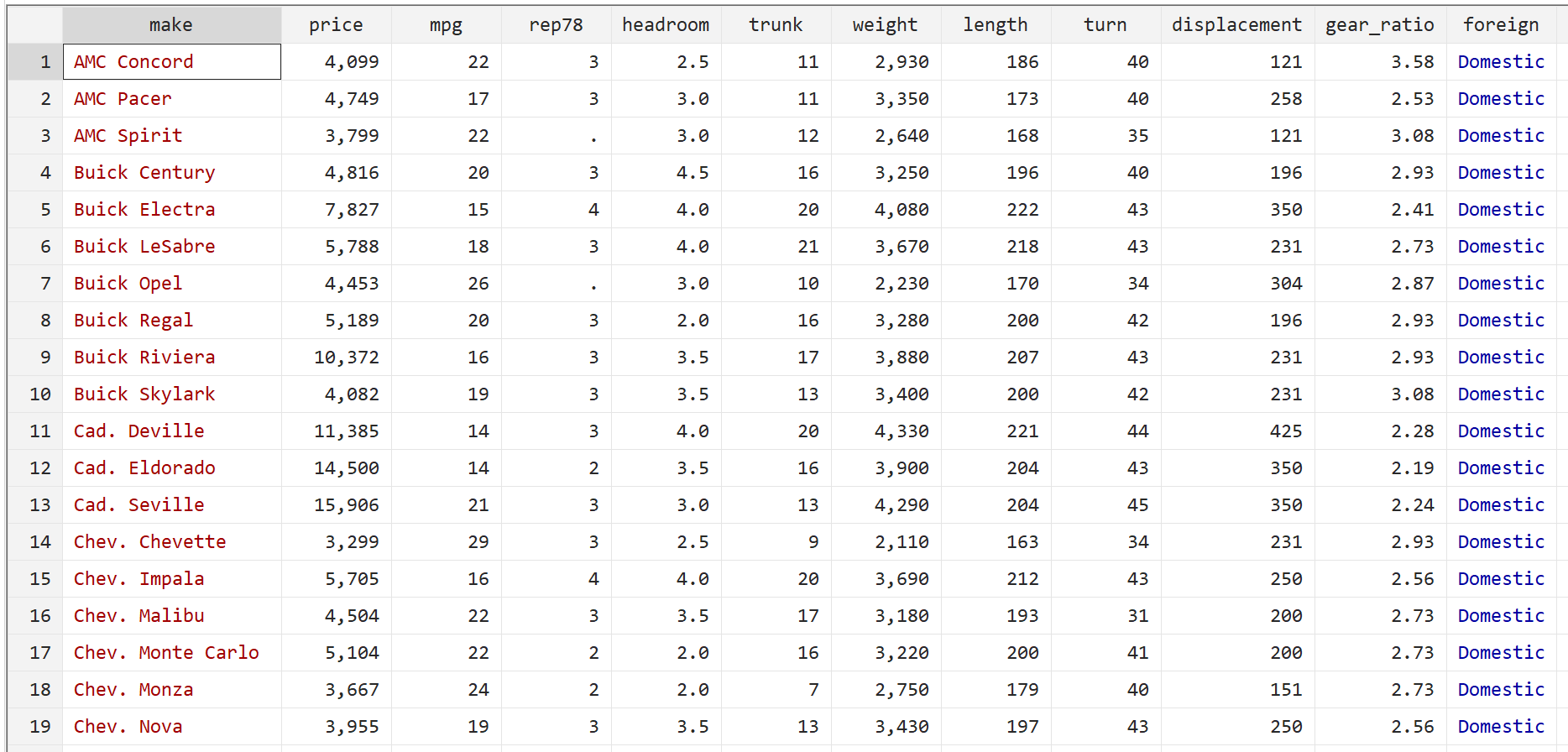
الخطوة 2: تنفيذ الانحدار الخطي المتعدد دون أخطاء قياسية قوية.

بعد ذلك، سوف نقوم بإدخال الأمر التالي لإجراء انحدار خطي متعدد باستخدام السعر كمتغير الاستجابة والميل لكل غالون والوزن كمتغيرات توضيحية:

سعر الانحدار ميلا في الغالون الوزن

الخطوة 3: تنفيذ الانحدار الخطي المتعدد باستخدام الأخطاء القياسية القوية.

سنقوم الآن بتنفيذ نفس الانحدار الخطي المتعدد، ولكن هذه المرة سنستخدم الأمر vce(robust) حتى تعرف Stata كيفية استخدام الأخطاء القياسية القوية:

سعر الانحدار ميلا في الغالون الوزن، vce (قوي)

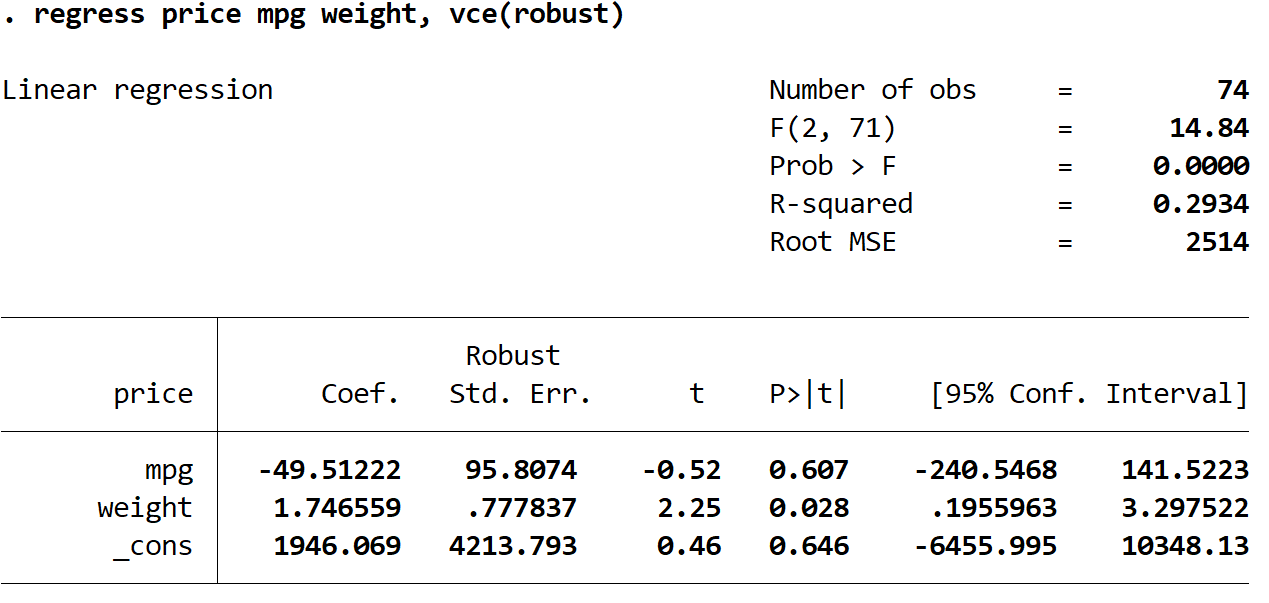
هناك بعض الأشياء المثيرة للاهتمام التي يجب ملاحظتها هنا:

1. بقيت تقديرات المعامل كما هي . عندما نستخدم أخطاء معيارية قوية، فإن تقديرات المعامل لا تتغير على الإطلاق. لاحظ أن تقديرات المعامل للميل لكل جالون والوزن والثابت هي كما يلي لكلا الانحدارين:

• ميلا في الغالون: -49.51222
• الوزن: 1.746559
• _ضد: 1946.069

2. لقد تغيرت الأخطاء القياسية . لاحظ أنه عندما استخدمنا أخطاء معيارية قوية، زادت الأخطاء المعيارية لكل تقدير من تقديرات المعامل.

ملحوظة: في معظم الحالات، ستكون الأخطاء القياسية القوية أكبر من الأخطاء القياسية العادية، ولكن في حالات نادرة من الممكن أن تكون الأخطاء القياسية القوية أصغر بالفعل.

3. لقد تغيرت إحصائية الاختبار لكل معامل. لاحظ أن القيمة المطلقة لكل إحصائية اختبار ، t ، قد انخفضت. في الواقع، يتم حساب إحصائية الاختبار على أنها المعامل المقدر مقسومًا على الخطأ المعياري. وبالتالي، كلما زاد الخطأ المعياري، قلت القيمة المطلقة لإحصائية الاختبار.

4. لقد تغيرت القيم الاحتمالية . لاحظ أن القيم الاحتمالية لكل متغير قد زادت أيضًا. وذلك لأن إحصائيات الاختبار الأصغر ترتبط بقيم p أكبر.

على الرغم من أن القيم p قد تغيرت لمعاملاتنا، إلا أن متغير mpg لا يزال غير ذي دلالة إحصائية عند α = 0.05 ولا يزال الوزن المتغير ذو دلالة إحصائية عند α = 0.05.