كيفية اختبار الحالة الطبيعية في ستاتا

تتطلب العديد من الاختبارات الإحصائيةتوزيع متغير واحد أو أكثر بشكل طبيعي حتى تكون نتائج الاختبار موثوقة.

يشرح هذا البرنامج التعليمي عدة طرق يمكنك استخدامها لاختبار الحالة الطبيعية بين المتغيرات في Stata.

لكل من هذه الطرق، سوف نستخدم مجموعة بيانات Stata المضمنة والتي تسمى auto . يمكنك تحميل مجموعة البيانات هذه باستخدام الأمر التالي:

الاستخدام التلقائي للنظام

الطريقة الأولى: الرسوم البيانية

إحدى الطرق غير الرسمية لمعرفة ما إذا كان المتغير يتم توزيعه بشكل طبيعي هي إنشاء رسم بياني لعرض توزيع المتغير.

إذا تم توزيع المتغير بشكل طبيعي، فيجب أن يأخذ الرسم البياني شكل “جرس” مع وجود قيم أكثر بالقرب من المركز وقيم أقل تقع على الأطراف.

يمكننا استخدام الأمر hist لإنشاء رسم بياني للإزاحة المتغيرة:

يتحرك التاريخ

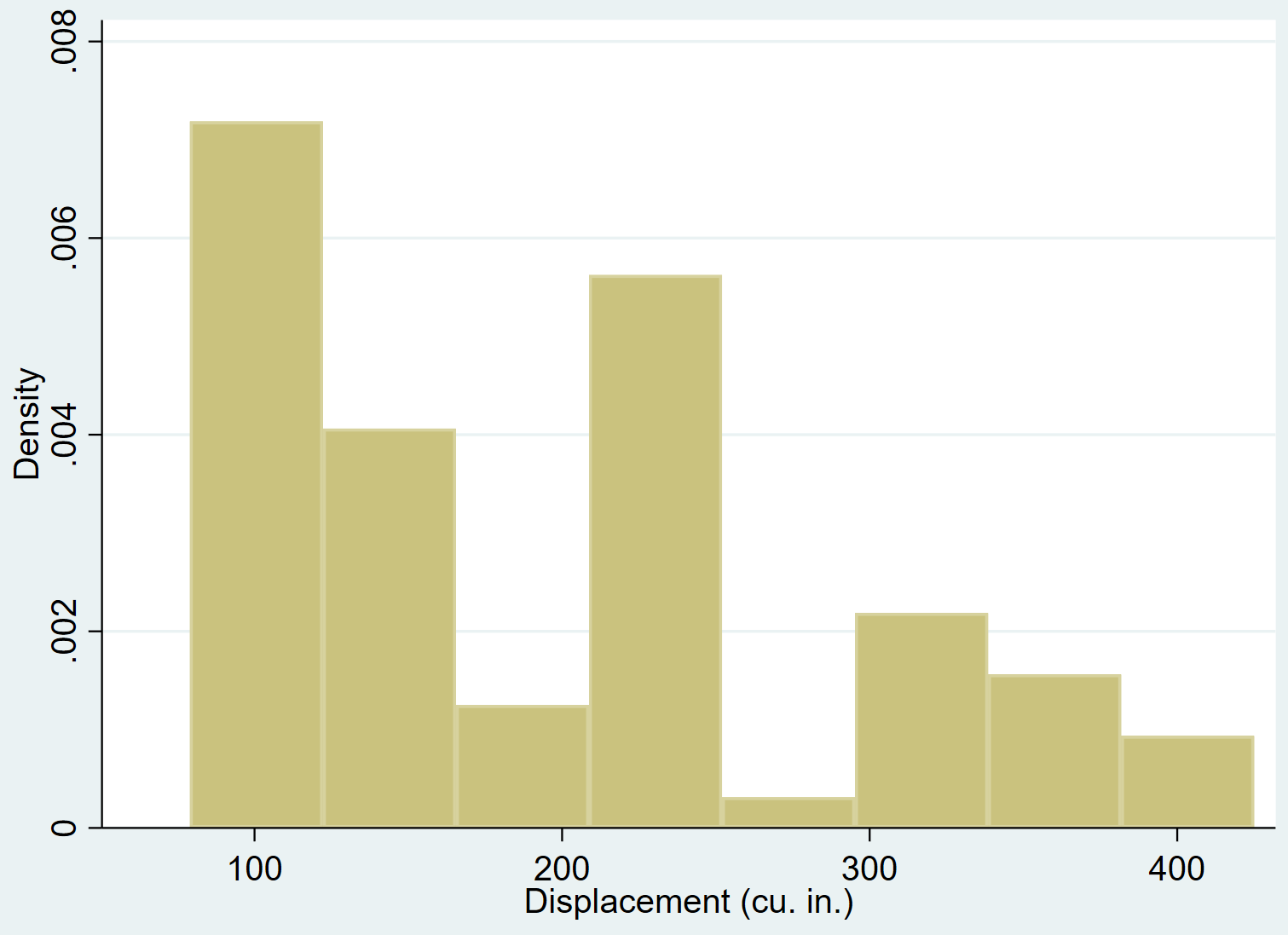
يمكننا إضافة منحنى الكثافة الطبيعي إلى الرسم البياني باستخدام الأمر العادي :

يتحرك التاريخ، طبيعي

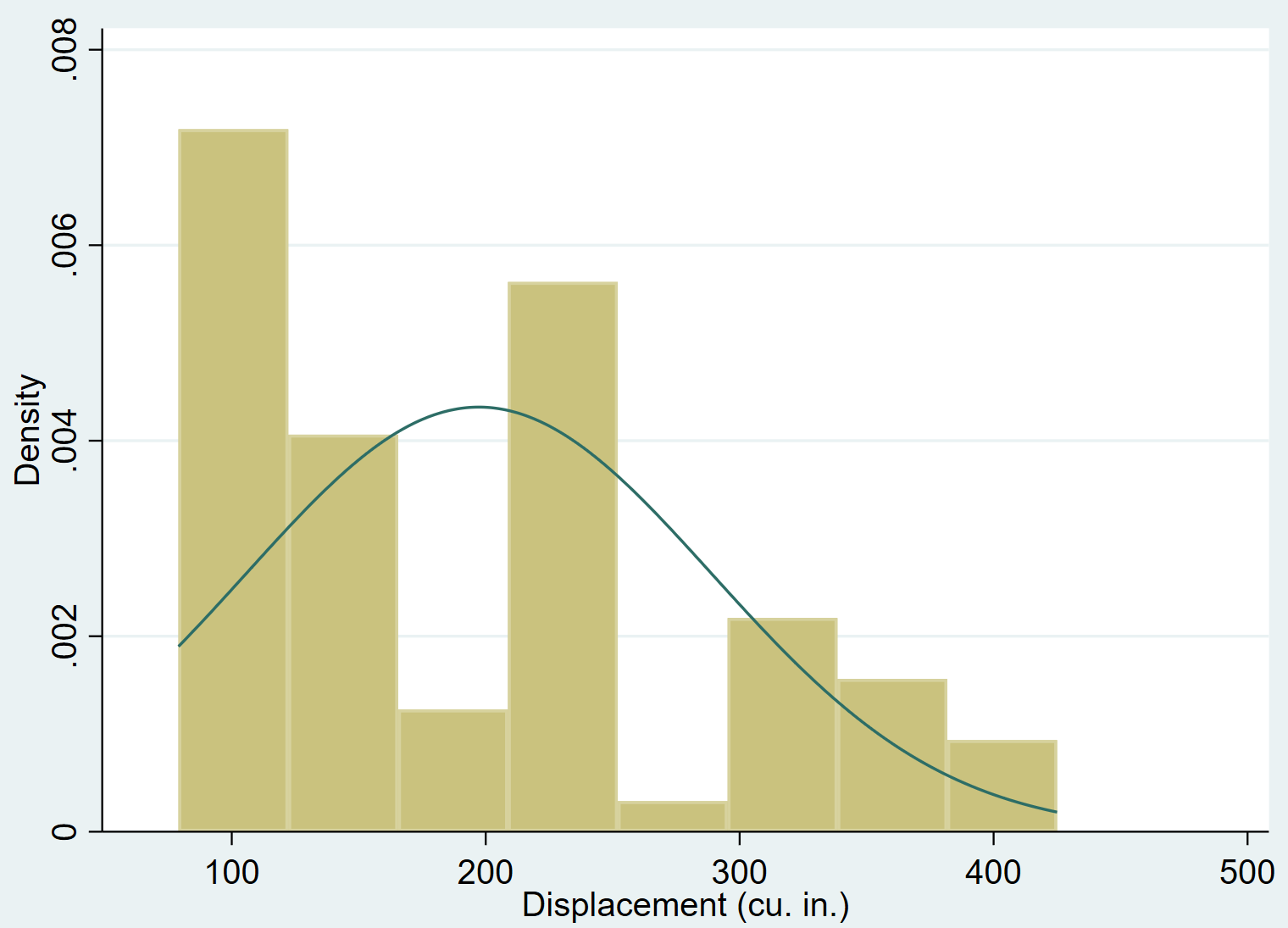
من الواضح تمامًا أن التحول المتغير ينحرف نحو اليمين (على سبيل المثال، تتركز معظم القيم على اليسار ويمتد “ذيل” طويل من القيم إلى اليمين) ولا يتبع التوزيع الطبيعي.

ذات صلة: التوزيعات المنحرفة لليسار واليمين

الطريقة الثانية: اختبار شابيرو ويلك

الطريقة الرسمية لاختبار الحالة الطبيعية هي استخدام اختبار شابيرو ويلك .

الفرضية الصفرية لهذا الاختبار هي أن المتغير يتم توزيعه بشكل طبيعي. إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية (تشمل الاختيارات الشائعة 0.01 و0.05 و0.10)، فيمكننا رفض فرضية العدم ونستنتج أن هناك أدلة كافية للتأكيد على أن المتغير غير موزع بشكل طبيعي .

*يمكن استخدام هذا الاختبار عندما يتراوح العدد الإجمالي للملاحظات بين 4 و2000.

يمكننا استخدام الأمر swilk لإجراء اختبار Shapiro-Wilk على الإزاحة المتغيرة:

حركة سلسة

وإليك كيفية تفسير نتيجة الاختبار:

Obs: 74. هذا هو عدد الملاحظات المستخدمة في الاختبار.

ث: 0.92542. هذه هي إحصائية الاختبار للاختبار.

المشكلة>z: 0.00031. هذه هي القيمة p المرتبطة بإحصائيات الاختبار.

وبما أن القيمة p أقل من 0.05، يمكننا رفض الفرضية الصفرية للاختبار. لدينا ما يكفي من الأدلة لنقول أن الإزاحة المتغيرة لا يتم توزيعها بشكل طبيعي.

يمكننا أيضًا إجراء اختبار Shapiro-Wilk على متغيرات متعددة مرة واحدة عن طريق إدراج متغيرات متعددة بعد أمر swilk :

طول النزوح ميلا في الغالون

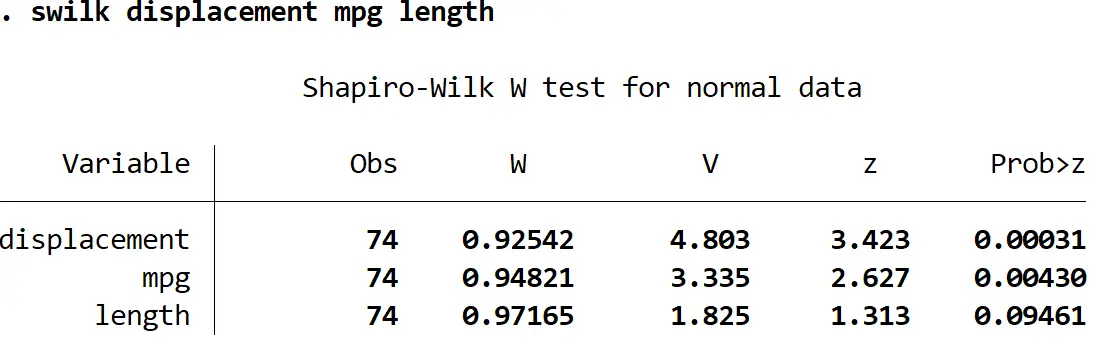
باستخدام مستوى دلالة 0.05، نستنتج أن الإزاحة والميل لكل جالون لا يتم توزيعهما بشكل طبيعي، ولكن ليس لدينا ما يكفي من الأدلة لنقول أن الطول غير موزع بشكل طبيعي.

الطريقة الثالثة: اختبار شابيرو-فرانسيا

هناك طريقة رسمية أخرى لاختبار الحالة الطبيعية وهي استخدام اختبار شابيرو-فرانسيا .

الفرضية الصفرية لهذا الاختبار هي أن المتغير يتم توزيعه بشكل طبيعي. إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية، فيمكننا رفض فرضية العدم ونستنتج أن هناك أدلة كافية للقول بأن المتغير غير موزع بشكل طبيعي.

*يمكن استخدام هذا الاختبار عندما يتراوح العدد الإجمالي للملاحظات بين 10 و5000.

يمكننا استخدام الأمر sfrancia لإجراء اختبار Shapiro-Wilk على الإزاحة المتغيرة:

سفرانيا متحركة

وإليك كيفية تفسير نتيجة الاختبار:

Obs: 74. هذا هو عدد الملاحظات المستخدمة في الاختبار.

دبليو: 0.93011. هذه هي إحصائية الاختبار للاختبار.

المشكلة>z: 0.00094. هذه هي القيمة p المرتبطة بإحصائيات الاختبار.

وبما أن القيمة p أقل من 0.05، يمكننا رفض الفرضية الصفرية للاختبار. لدينا ما يكفي من الأدلة لنقول أن الإزاحة المتغيرة لا يتم توزيعها بشكل طبيعي.

على غرار اختبار شابيرو-ويلك، يمكنك إجراء اختبار شابيرو-فرانسيا على متغيرات متعددة في وقت واحد عن طريق إدراج متغيرات متعددة بعد الأمر sfrancia .

الطريقة الرابعة: اختبار الانحراف والتفرطح

هناك طريقة أخرى لاختبار الحالة الطبيعية وهي استخدام اختبار الانحراف والتفرطح ، الذي يحدد ما إذا كان الانحراف والتفرطح للمتغير متوافقين مع التوزيع الطبيعي أم لا.

الفرضية الصفرية لهذا الاختبار هي أن المتغير يتم توزيعه بشكل طبيعي. إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية، فيمكننا رفض فرضية العدم ونستنتج أن هناك أدلة كافية للقول بأن المتغير غير موزع بشكل طبيعي.

*يتطلب هذا الاختبار استخدام 8 ملاحظات على الأقل.

يمكننا استخدام الأمر sktest لإجراء اختبار الانحراف والتفرطح على الإزاحة المتغيرة:

تحريك الاختبار

وإليك كيفية تفسير نتيجة الاختبار:

Obs: 74. هذا هو عدد الملاحظات المستخدمة في الاختبار.

صفة تشي (2): 5.81. هذه هي إحصائية اختبار مربع كاي للاختبار.

مشكلة>chi2: 0.0547. هذه هي القيمة p المرتبطة بإحصائيات الاختبار.

وبما أن القيمة p لا تقل عن 0.05، فإننا نفشل في رفض الفرضية الصفرية للاختبار. ليس لدينا ما يكفي من الأدلة لنقول أن الحركات ليست موزعة بشكل طبيعي.

على غرار اختبارات الحالة الطبيعية الأخرى، يمكنك إجراء اختبار الانحراف والتفرطح على متغيرات متعددة في وقت واحد عن طريق إدراج متغيرات متعددة بعد أمر sktest .