كيفية إجراء الانحدار الخطي البسيط في ستاتا

الانحدار الخطي البسيط هو أسلوب يمكنك استخدامه لفهم العلاقة بين المتغير التوضيحي x ومتغير الاستجابة y.

يشرح هذا البرنامج التعليمي كيفية إجراء انحدار خطي بسيط في Stata.

مثال: الانحدار الخطي البسيط في ستاتا

لنفترض أننا نريد أن نفهم العلاقة بين وزن السيارة وعدد الأميال التي تقطعها لكل جالون. لاستكشاف هذه العلاقة، يمكننا إجراء انحدار خطي بسيط باستخدام الوزن كمتغير توضيحي والأميال لكل جالون كمتغير الاستجابة.

أكمل الخطوات التالية في Stata لإجراء انحدار خطي بسيط باستخدام مجموعة البيانات المسماة auto ، والتي تحتوي على بيانات عن 74 سيارة مختلفة.

الخطوة 1: تحميل البيانات.

قم بتحميل البيانات عن طريق كتابة ما يلي في مربع الأمر:

استخدم https://www.stata-press.com/data/r13/auto

الخطوة 2: احصل على ملخص البيانات.

احصل على فهم سريع للبيانات التي تتعامل معها عن طريق كتابة ما يلي في مربع الأوامر:

كي تختصر

يمكننا أن نرى أن هناك 12 متغيرًا مختلفًا في مجموعة البيانات، لكن المتغيرين الوحيدين اللذين نهتم بهما هما ميل لكل جالون ووزن .

الخطوة 3: تصور البيانات.

قبل إجراء انحدار خطي بسيط، دعونا أولاً ننشئ مخططًا مبعثرًا للوزن مقابل ميلا في الغالون حتى نتمكن من تصور العلاقة بين هذين المتغيرين والتحقق من وجود قيم متطرفة واضحة. اكتب ما يلي في مربع الأوامر لإنشاء مخطط مبعثر:

تشتت الوزن ميلا في الغالون

وينتج عن ذلك المخطط المبعثر التالي:

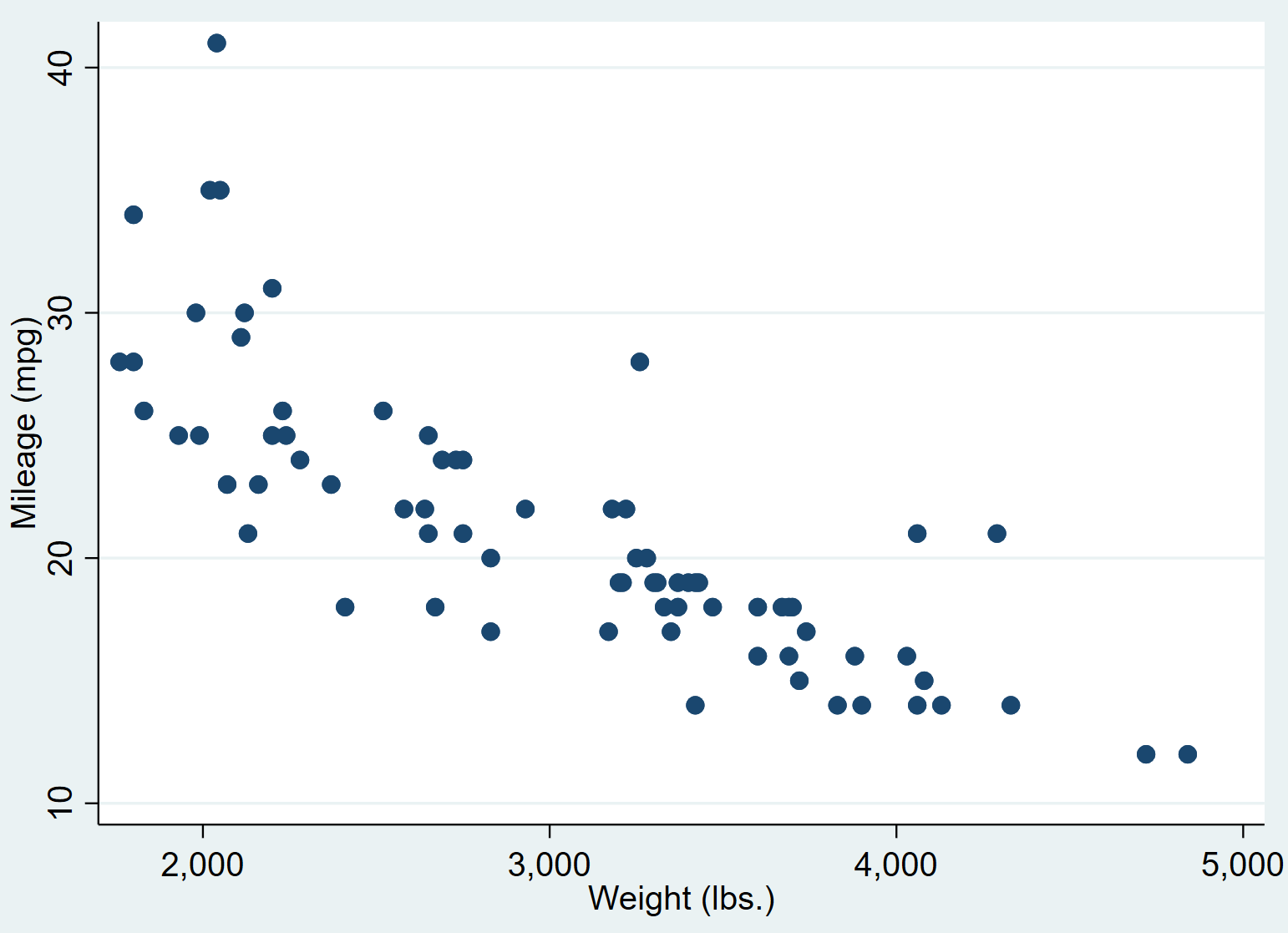
يمكننا أن نرى أن السيارات ذات الأوزان الأعلى تميل إلى قطع أميال أقل لكل جالون. لتحديد هذه العلاقة، سنقوم الآن بإجراء انحدار خطي بسيط.

الخطوة 4: إجراء الانحدار الخطي البسيط.

اكتب ما يلي في مربع الأوامر لإجراء انحدار خطي بسيط باستخدام الوزن كمتغير توضيحي وmpg كمتغير الاستجابة.

تراجع الوزن إلى ميلا في الغالون

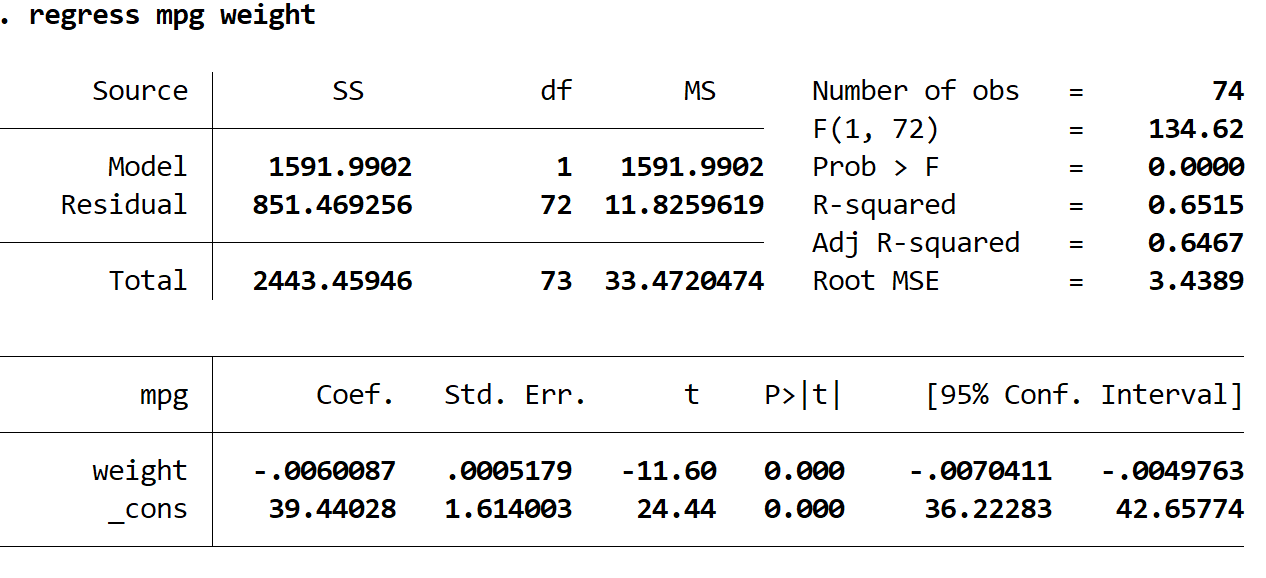
إليك كيفية تفسير الأرقام الأكثر إثارة للاهتمام في النتيجة:

R تربيع: 0.6515. وهي نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بالمتغير التوضيحي. في هذا المثال، يمكن تفسير 65.15% من التباين في الميل لكل جالون بالوزن.

معامل (الوزن): -0.006. وهذا يخبرنا بمتوسط التغير في متغير الاستجابة المرتبط بزيادة وحدة واحدة في المتغير التوضيحي. في هذا المثال، كل رطل واحد زيادة في الوزن يرتبط بانخفاض قدره 0.006 ميلا في الغالون في المتوسط.

معامل التحويل (_cons): 39.44028. وهذا يخبرنا بالقيمة المتوسطة لمتغير الاستجابة عندما يكون المتغير التوضيحي صفراً. في هذا المثال، متوسط ميل لكل جالون هو 39.44028 عندما يكون وزن السيارة صفرًا. هذا ليس منطقيًا حقًا للتفسير نظرًا لأن وزن السيارة لا يمكن أن يكون صفرًا، لكن الرقم 39.44028 ضروري لتشكيل معادلة الانحدار.

ف>|ر| (الوزن): 0.000. هذه هي القيمة p المرتبطة بإحصائيات اختبار الوزن. في هذه الحالة، وبما أن هذه القيمة أقل من 0.05، يمكننا أن نستنتج أن هناك علاقة ذات دلالة إحصائية بين الوزن والميل لكل جالون.

معادلة الانحدار: أخيراً يمكننا تكوين معادلة انحدار باستخدام قيمتي المعاملين. وفي هذه الحالة ستكون المعادلة:

ميل لكل جالون متوقع = 39.44028 – 0.0060087*(الوزن)

يمكننا استخدام هذه المعادلة للعثور على ميلا في الغالون المتوقع للسيارة، نظرا لوزنها. على سبيل المثال، السيارة التي تزن 4000 رطل يجب أن يكون لديها ميل لكل جالون يبلغ 15405 ميلاً في الغالون:

ميل لكل جالون متوقع = 39.44028 – 0.0060087*(4000) = 15.405

الخطوة 5: الإبلاغ عن النتائج.

وأخيرًا، نريد الإبلاغ عن نتائج الانحدار الخطي البسيط. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء الانحدار الخطي لتحديد العلاقة بين وزن السيارة وعدد الأميال التي تقطعها لكل جالون. تم استخدام عينة مكونة من 74 سيارة في التحليل.

أظهرت النتائج أن هناك علاقة ذات دلالة إحصائية بين الوزن والميل لكل جالون (t = -11.60، p <0.0001) وأن الوزن يمثل 65.15% من التباين الموضح في الميل لكل جالون.

وتبين أن معادلة الانحدار هي:

ميل لكل جالون متوقع = 39.44 – 0.006 (الوزن)

وارتبط كل رطل إضافي بانخفاض قدره -0.006 ميل في المتوسط للغالون الواحد.