كيفية اختبار الخطية المتعددة في spss

تحدث العلاقة الخطية المتعددة في تحليل الانحدار عندما يرتبط متغيران أو أكثر من متغيرات التوقع ارتباطًا وثيقًا ببعضهما البعض، بحيث لا يوفران معلومات فريدة أو مستقلة في نموذج الانحدار. إذا كانت درجة الارتباط عالية بما يكفي بين المتغيرات، فقد يتسبب ذلك في حدوث مشكلات عند ملاءمة نموذج الانحدار وتفسيره.

تتمثل إحدى طرق اكتشاف التعددية الخطية في استخدام مقياس يُعرف باسم عامل تضخم التباين (VIF) ، والذي يقيس الارتباط وقوة الارتباط بين متغيرات التوقع في نموذج الانحدار.

يشرح هذا البرنامج التعليمي كيفية استخدام VIF للكشف عن العلاقة الخطية المتعددة في تحليل الانحدار في برنامج SPSS.

مثال: العلاقة الخطية المتعددة في SPSS

لنفترض أن لدينا مجموعة البيانات التالية التي توضح درجة الاختبار لـ 10 طلاب بالإضافة إلى عدد الساعات التي قضوها في الدراسة، وعدد الاختبارات التدريبية التي أجروها، ودرجاتهم الحالية في الدورة:

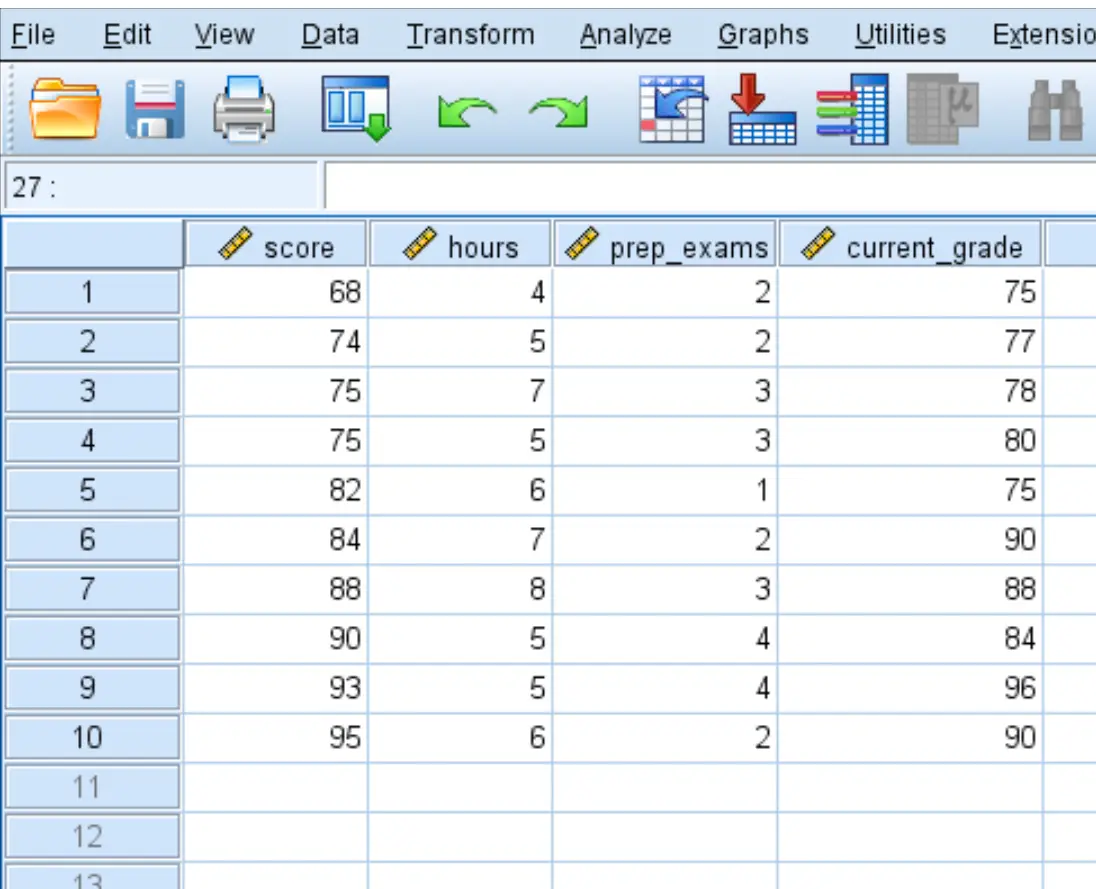
نود إجراء انحدار خطي باستخدام النتيجة كمتغير الاستجابة والساعات و prep_exams و current_grade كمتغيرات متوقعة، ولكننا نريد التأكد من أن متغيرات التنبؤ الثلاثة ليست مرتبطة بشكل كبير.

لتحديد ما إذا كانت العلاقة الخطية المتعددة تمثل مشكلة، يمكننا إنتاج قيم VIF لكل من متغيرات التوقع.

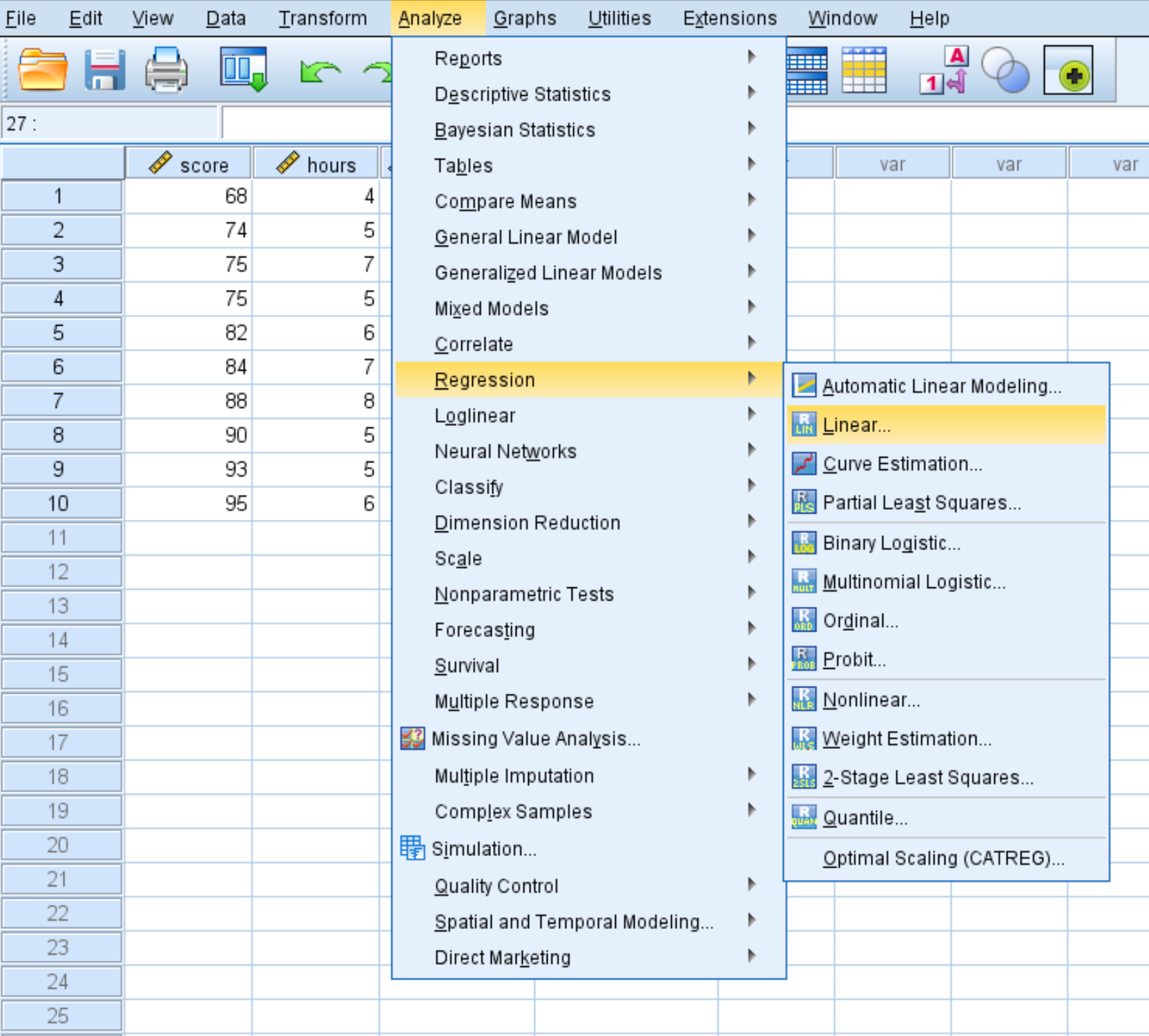
للقيام بذلك، انقر فوق علامة التبويب تحليل ، ثم الانحدار ، ثم الخطي :

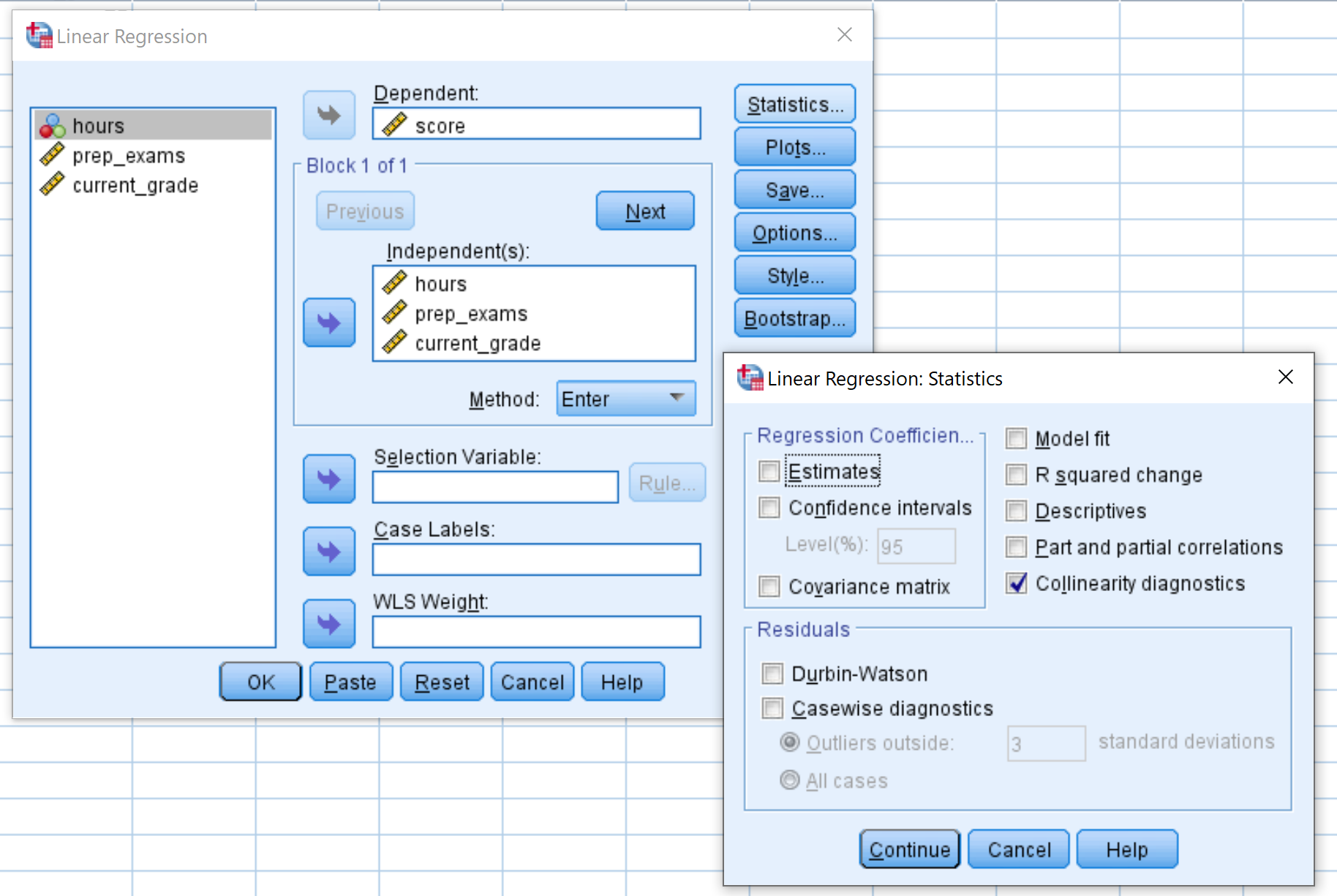
في النافذة الجديدة التي تظهر، اسحب النتيجة إلى المربع المسمى “معال” واسحب متغيرات التوقع الثلاثة إلى المربع المسمى “مستقل (مستقل)”. ثم انقر فوق الإحصائيات وتأكد من تحديد المربع بجوار تشخيصات العلاقة الخطية المتداخلة . ثم انقر فوق “متابعة” . ثم انقر فوق موافق .

بعد النقر فوق موافق ، يظهر الجدول التالي موضحًا قيمة VIF لكل متغير متنبئ:

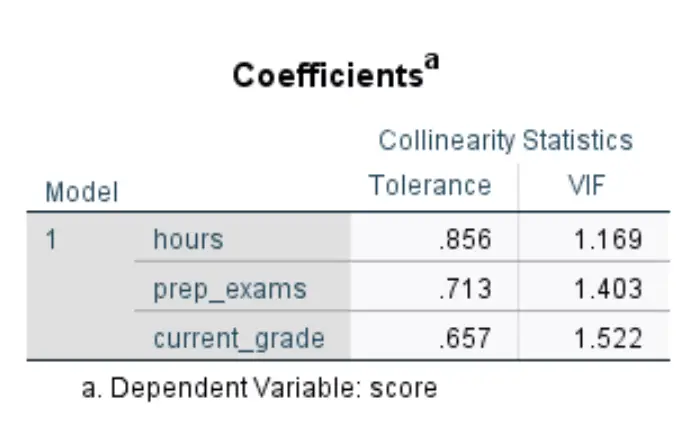
قيم VIF لكل من متغيرات التوقع هي كما يلي:

• الساعات: 1,169
• الامتحانات الإعدادية: 1,403
• النتيجة الحالية: 1.522

تبدأ قيمة VIF عند 1 وليس لها حد أعلى. القاعدة العامة لتفسير VIFs هي:

• تشير القيمة 1 إلى عدم وجود ارتباط بين متغير توقع معين وأي متغير توقع آخر في النموذج.
• تشير القيمة بين 1 و5 إلى وجود علاقة معتدلة بين متغير متنبئ معين ومتغيرات تنبؤية أخرى في النموذج، ولكنها في كثير من الأحيان ليست شديدة بما يكفي لتتطلب اهتمامًا خاصًا.
• تشير القيمة الأكبر من 5 إلى وجود علاقة جدية محتملة بين متغير توقع معين ومتغيرات توقع أخرى في النموذج. في هذه الحالة، من المحتمل أن تكون تقديرات المعامل والقيم الاحتمالية في نتائج الانحدار غير موثوقة.

يمكننا أن نرى أن أيا من قيم VIF لمتغيرات التوقع في هذا المثال أكبر من 5، مما يشير إلى أن التعددية الخطية لن تكون مشكلة في نموذج الانحدار.