ما هو توزيع العينات؟

تخيل أن هناك عددًا يبلغ 10000 دولفين وأن متوسط وزن الدلفين في تلك المجموعة يبلغ 300 رطل.

إذا أخذنا عينة عشوائية بسيطة مكونة من 50 دلفينًا من هذه المجموعة، فقد نجد أن متوسط وزن الدلافين في هذه العينة هو 305 أرطال.

ثم، إذا أخذنا عينة عشوائية بسيطة أخرى مكونة من 50 دولفينًا، فقد نجد أن متوسط وزن الدلافين في هذه العينة هو 295 رطلاً.

كلما أخذنا عينة عشوائية بسيطة مكونة من 50 دولفين، فمن المرجح أن متوسط وزن الدلافين في العينة يقترب من متوسط عدد السكان البالغ 300 رطل، ولكن ليس 300 رطل بالضبط.

لنتخيل أننا أخذنا 200 عينة عشوائية بسيطة من 50 دلفينًا من هذه المجموعة وقمنا بإنشاء رسم بياني لمتوسط وزن كل عينة:

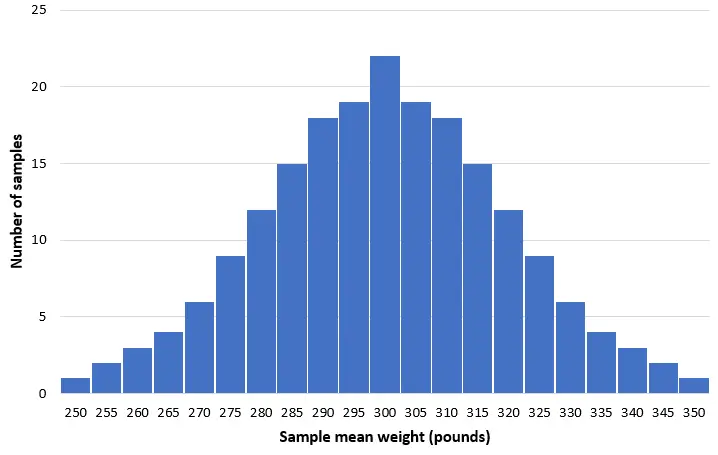
في معظم العينات، سيكون متوسط الوزن قريبًا من 300 رطل. وفي حالات نادرة، قد نأخذ عينة كاملة من الدلافين الصغيرة التي يبلغ متوسط وزنها 250 رطلاً فقط. أو قد نأخذ عينة مليئة بالدلافين قارورية الأنف التي يبلغ متوسط وزنها 350 رطلاً. بشكل عام، سيكون توزيع متوسطات العينة طبيعيًا تقريبًا، حيث يقع مركز التوزيع في المركز الحقيقي للسكان.

يُعرف هذا التوزيع لمتوسطات العينة بتوزيع المعاينة للمتوسط وله الخصائص التالية:

_μx = μ

حيث μ _x هو متوسط العينة و μ هو متوسط السكان.

_σx = σ/√n

حيث σ _x هو الانحراف المعياري للعينة، σ هو الانحراف المعياري للسكان، و n هو حجم العينة.

على سبيل المثال، في هذه المجموعة من الدلافين، نعلم أن متوسط الوزن هو μ = 300. لذا فإن متوسط توزيع العينات هو μ _x = 300 .

لنفترض أننا نعلم أيضًا أن الانحراف المعياري للسكان هو 18 رطلاً. وبالتالي فإن الانحراف المعياري للعينة هو σ _x = 18/ √50 = 2.546 .

توزيع العينات نسبة

خذ بعين الاعتبار نفس عدد السكان البالغ 10000 دولفين. افترض أن 10% من الدلافين سوداء اللون والباقي رمادية اللون. لنفترض أننا أخذنا عينة عشوائية بسيطة مكونة من 50 دولفينًا ووجدنا أن 14% من الدلافين في تلك العينة سوداء اللون. بعد ذلك، أخذنا عينة عشوائية بسيطة أخرى مكونة من 50 دولفينًا ووجدنا أن 8% من الدلافين في هذه العينة سوداء اللون.

تخيل أننا أخذنا 200 عينة عشوائية بسيطة من 50 دلفينًا من هذه المجموعة وقمنا بإنشاء رسم بياني لنسبة الدلافين السوداء في كل عينة:

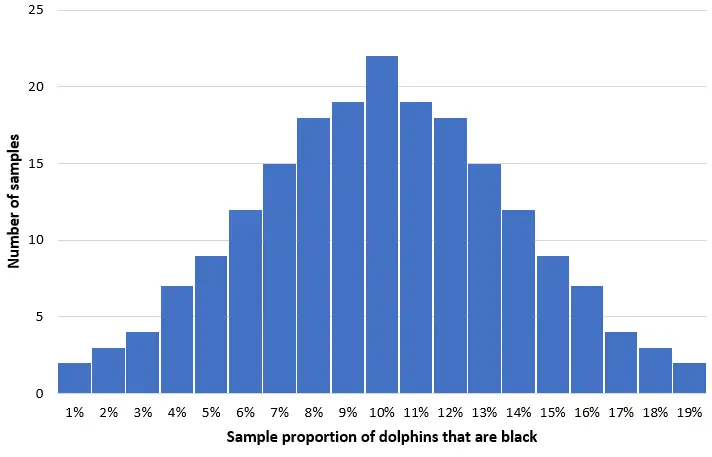
في معظم العينات، ستكون نسبة الدلافين السوداء قريبة من التعداد الفعلي البالغ 10%. سيكون توزيع نسبة العينة من الدلافين السوداء طبيعيًا تقريبًا، حيث يقع مركز التوزيع في المركز الحقيقي للسكان.

يُعرف هذا التوزيع لنسب العينة بتوزيع المعاينة التناسبي وله الخصائص التالية:

_μp = P

حيث p هي نسبة العينة و P هي نسبة السكان.

σ _ع = √ (ف)(1-ف) / ن

حيث P هي نسبة السكان و n هو حجم العينة.

على سبيل المثال، في مجموعة الدلافين هذه، نعلم أن النسبة الحقيقية للدلافين السوداء هي 10% = 0.1. وبالتالي، فإن متوسط التوزيع التناسبي للعينات هو _μp = 0.1 .

لنفترض أننا نعلم أيضًا أن الانحراف المعياري للسكان هو 18 رطلاً. وبالتالي، فإن الانحراف المعياري للعينة هو σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

إرساء الحياة الطبيعية

لاستخدام الصيغ أعلاه، يجب أن يكون توزيع العينات طبيعيا.

وفقا لنظرية الحد المركزي ، فإن توزيع المعاينة لمتوسط العينة يكون طبيعيا تقريبا إذا كان حجم العينة كبيرا بما فيه الكفاية، حتى لو كان توزيع السكان غير طبيعي . في معظم الحالات، نعتبر حجم العينة الذي يبلغ 30 أو أكثر كبيرًا بدرجة كافية.

يكون توزيع العينة لنسبة العينة طبيعيًا تقريبًا إذا كان العدد المتوقع للنجاحات والإخفاقات لا يقل عن 10.

أمثلة

يمكننا استخدام توزيعات العينات لحساب الاحتمالات.

مثال 1: يقوم جهاز معين بإنشاء ملفات تعريف الارتباط. ينحرف توزيع وزن ملفات تعريف الارتباط هذه إلى اليمين بمتوسط 10 أونصات وانحراف معياري قدره 2 أونصة. إذا أخذنا عينة عشوائية بسيطة مكونة من 100 ملف تعريف ارتباط تم إنتاجها بواسطة هذا الجهاز، فما احتمال أن يكون متوسط وزن ملفات تعريف الارتباط في هذه العينة أقل من 9.8 أوقية؟

الخطوة 1: تأسيس الحياة الطبيعية.

نحن بحاجة للتأكد من أن توزيع العينات لوسائل العينة طبيعي. وبما أن حجم العينة لدينا أكبر من أو يساوي 30، وفقًا لنظرية الحد المركزي، فيمكننا أن نفترض أن توزيع المعاينة لمتوسطات العينة طبيعي.

الخطوة الثانية: إيجاد المتوسط والانحراف المعياري لتوزيع العينات.

_μx = μ

_σx = σ/√n

μ _س = 10 أوقية

σ _س = 2/ √100 = 2/10 = 0.2 أونصة

الخطوة 3: استخدم حاسبة منطقة Z-Score لتحديد احتمالية أن يكون متوسط وزن ملف تعريف الارتباط في هذه العينة أقل من 9.8 أوقية.

أدخل الأرقام التالية في حاسبة منطقة نقاط Z. يمكنك ترك “Raw Score 2” فارغًا نظرًا لأننا نجد رقمًا واحدًا فقط في هذا المثال.

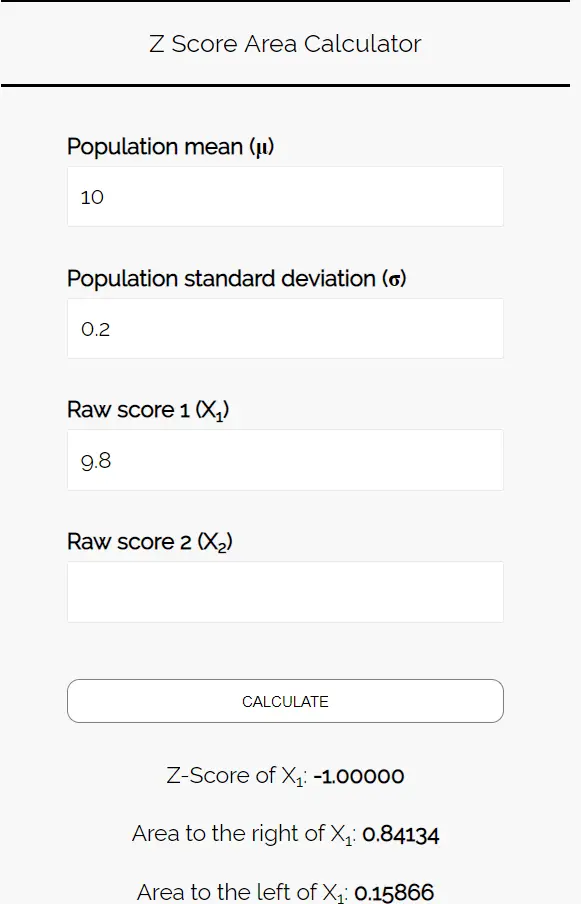
وبما أننا نريد معرفة احتمال أن يكون متوسط وزن قطع البسكويت في هذه العينة أقل من 9.8 أوقية، فإننا مهتمون بالمساحة الموجودة على يسار 9.8. تخبرنا الآلة الحاسبة أن هذا الاحتمال هو 0.15866 .

مثال 2: وفقًا لدراسة أجريت على مستوى المدرسة، فإن 87% من الطلاب في مدرسة معينة يفضلون البيتزا على الآيس كريم. لنفترض أننا أخذنا عينة عشوائية بسيطة من 200 طالب. ما احتمال أن تكون نسبة الطلاب الذين يفضلون البيتزا أقل من 85%؟

الخطوة 1: تأسيس الحياة الطبيعية.

تذكر أن توزيع العينة لنسبة العينة يكون طبيعيًا تقريبًا إذا كان العدد المتوقع لـ “النجاحات” و”الإخفاقات” هو 10 على الأقل.

وفي هذه الحالة فإن العدد المتوقع للطلاب الذين سيفضلون البيتزا هو 87% * 200 طالب = 174 طالبًا. العدد المتوقع للطلاب الذين لن يفضلوا البيتزا هو 13% * 200 طالب = 26 طالب. وبما أن كلا الرقمين يبلغان 10 على الأقل، يمكننا أن نفترض أن توزيع العينة لنسبة الطلاب الذين يفضلون البيتزا طبيعي تقريبًا.

الخطوة الثانية: إيجاد المتوسط والانحراف المعياري لتوزيع العينات.

_μp = P

σ _ع = √ (ف)(1-ف) / ن

_μp = 0.87

σ _ع = √ (0.87)(1-0.87) / 200 = 0.024

الخطوة 3: استخدم حاسبة منطقة Z-Score لتحديد احتمال أن تكون نسبة الطلاب الذين يفضلون البيتزا أقل من 85%.

أدخل الأرقام التالية في حاسبة منطقة نقاط Z. يمكنك ترك “Raw Score 2” فارغًا نظرًا لأننا نجد رقمًا واحدًا فقط في هذا المثال.

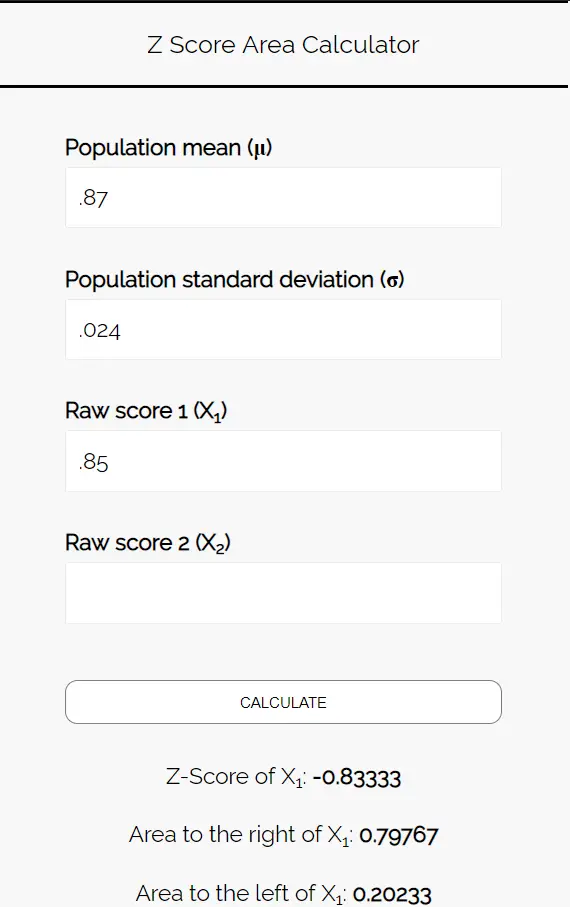
وبما أننا نريد معرفة احتمال أن تكون نسبة الطلاب الذين يفضلون البيتزا أقل من 85%، فإننا مهتمون بالمنطقة الواقعة على يسار 0.85. تخبرنا الآلة الحاسبة أن هذا الاحتمال هو 0.20233 .