التوزيع المتماثل: التعريف + الأمثلة

في الإحصاء، التوزيع المتماثل هو التوزيع الذي يعكس فيه الجانبان الأيسر والأيمن بعضهما البعض.

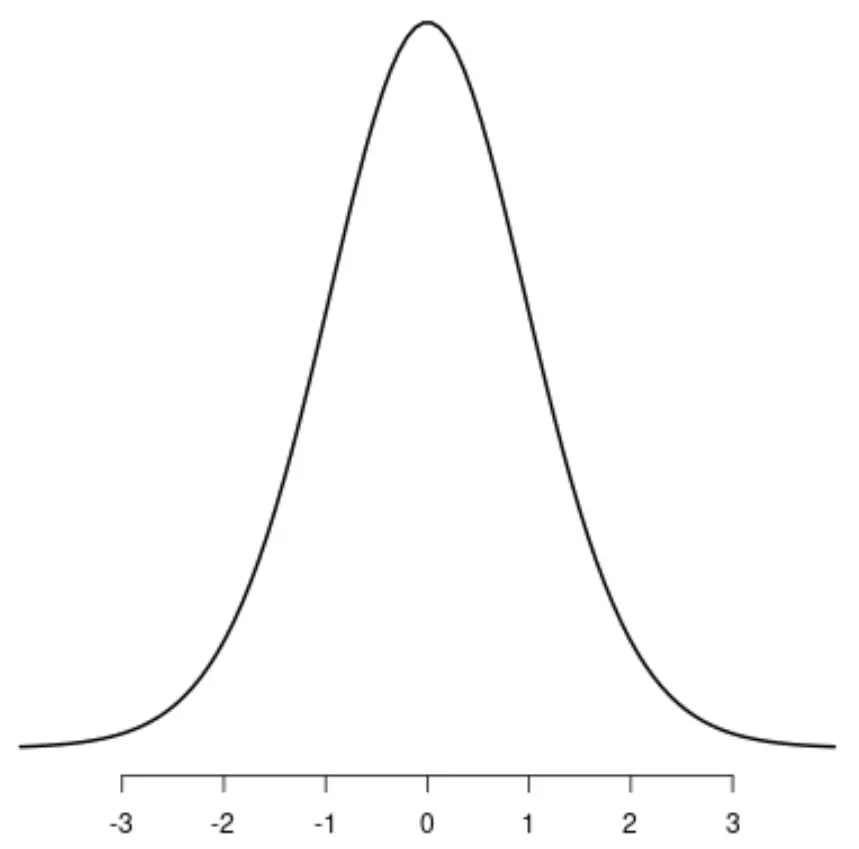
التوزيع المتماثل الأكثر شهرة هوالتوزيع الطبيعي ، الذي له شكل جرس مميز.

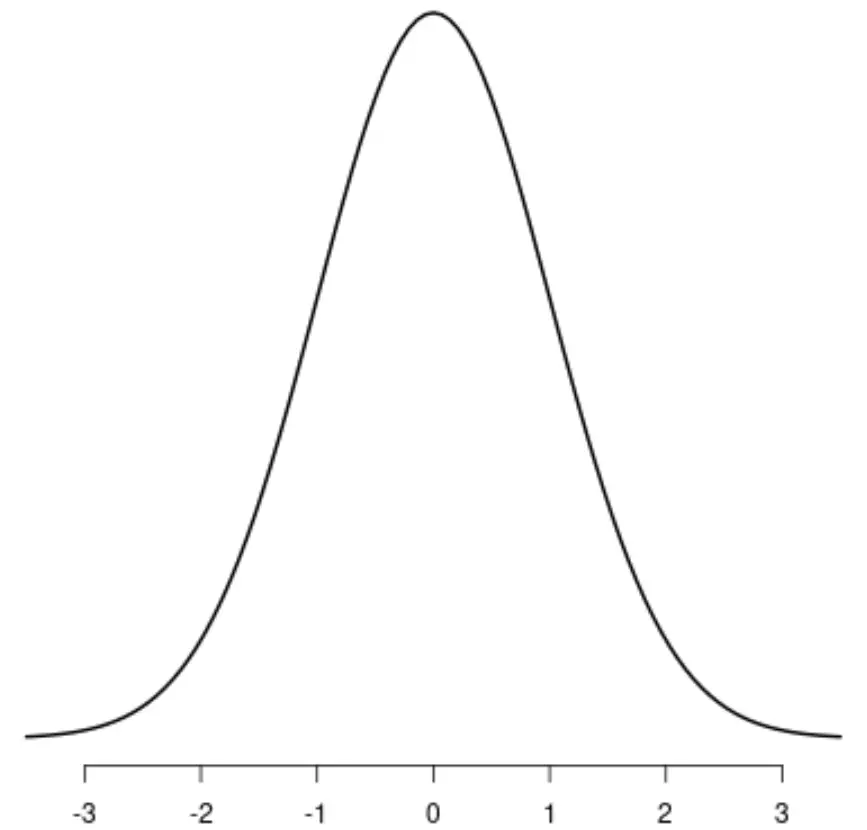
إذا كنت تريد رسم خط أسفل مركز التوزيع، فإن الجانبين الأيسر والأيمن للتوزيع سيعكسان بعضهما البعض بشكل مثالي:

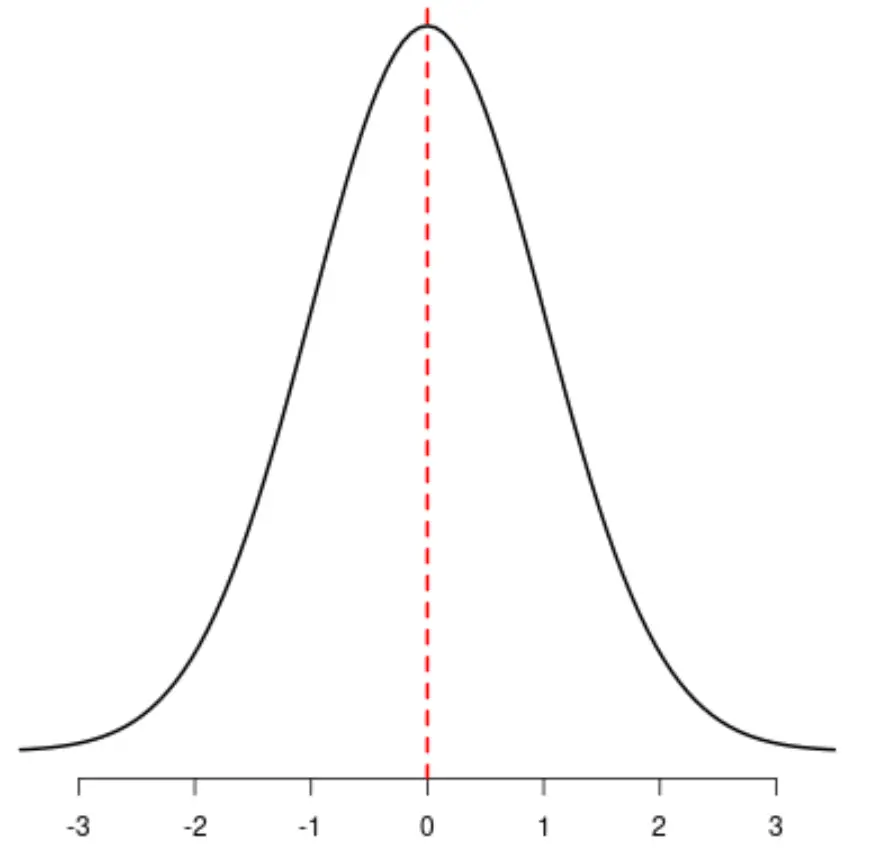
في الإحصاء، الانحراف هو وسيلة لوصف تماثل التوزيع. يمكن أن تكون هذه القيمة سالبة أو صفرية أو موجبة.

بالنسبة للتوزيعات المتماثلة، يكون عدم التماثل صفرًا.

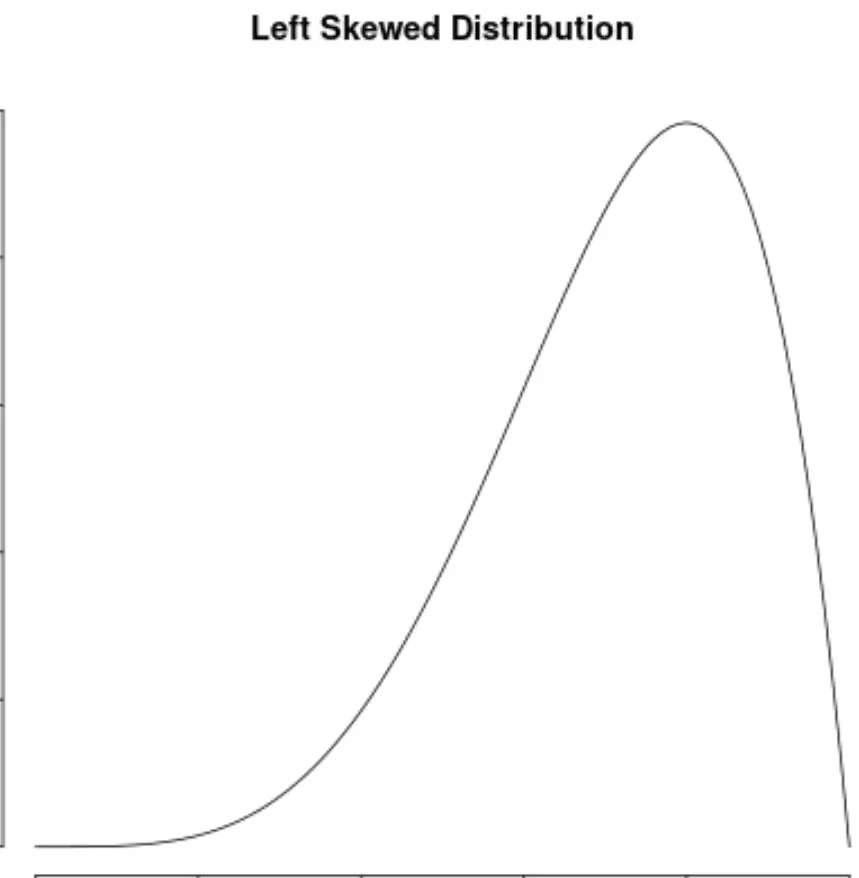
وهذا يتناقض مع التوزيعات المنحرفة إلى اليسار، والتي لها انحراف سلبي:

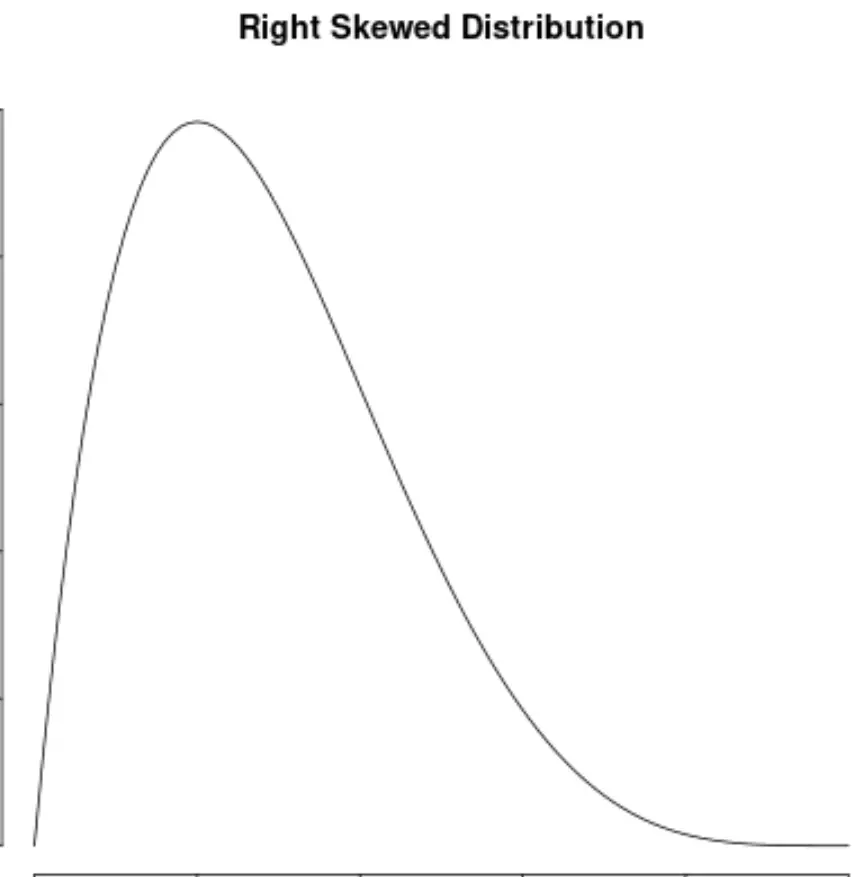
وهذا يتناقض أيضًا مع التوزيعات المنحرفة لليمين، والتي لها انحراف إيجابي:

خصائص التوزيعات المتماثلة

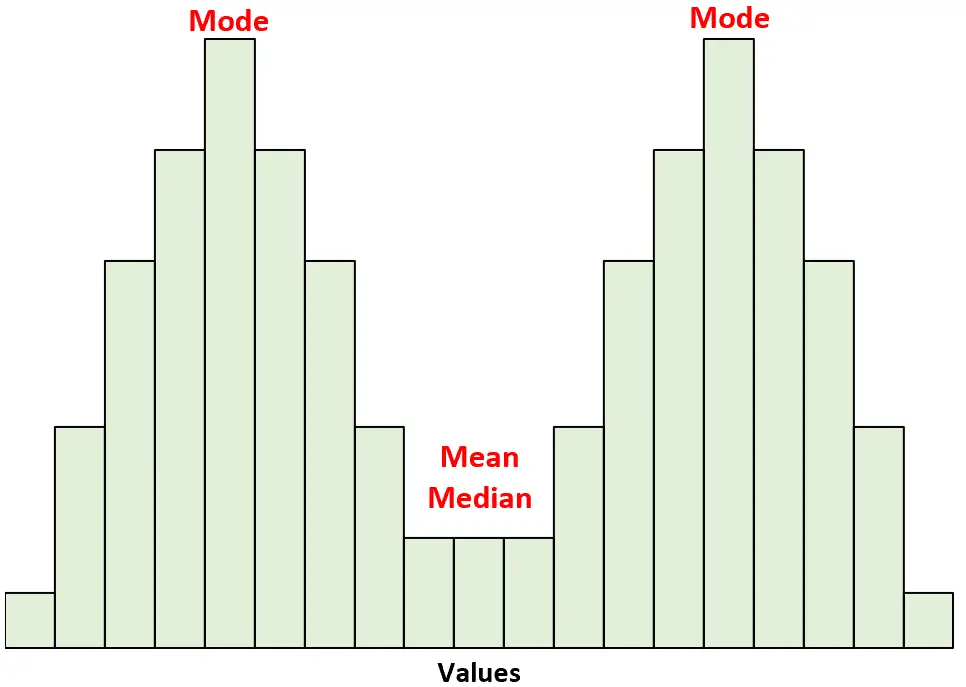
في التوزيع المتماثل، يكون المتوسط والوسيط والمنوال متساويين.

تذكر التعريفات التالية لكل منها:

• المتوسط: القيمة المتوسطة.
• الوسيط: القيمة المتوسطة.
• الوضع: القيمة التي تظهر في أغلب الأحيان.

وفي التوزيع المتماثل تكون كل قيمة من هذه القيم مساوية للأخرى.

وفي كل من الأمثلة حتى الآن، استخدمنا التوزيعات الأحادية الواسطة كأمثلة – توزيعات ذات “ذروة” واحدة فقط. ومع ذلك، يمكن للتوزيع أيضًا أن يكون ثنائي الشكل ومتماثلًا.

التوزيع الثنائي هو التوزيع الذي له قمتين.

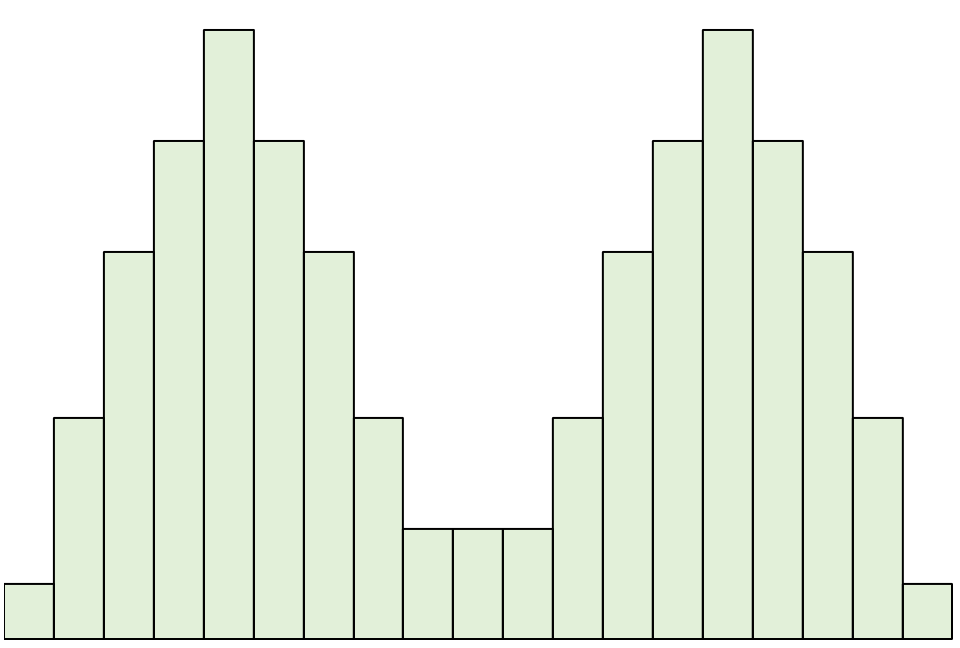
لاحظ أنه إذا رسمنا خطًا أسفل مركز هذا التوزيع، فسيظل الجانبان الأيسر والأيمن يعكسان بعضهما البعض.

بالنسبة لهذه التوزيعات، فإن المتوسط والوسيط متساويان. ومع ذلك، فإن الوضع يكمن في كلا القمم.

أمثلة أخرى على التوزيعات المتماثلة

إلى جانب التوزيع الطبيعي، التوزيعات التالية متماثلة أيضًا:

التوزيع ر

التوزيع الموحد

توزيع كوشي

إذا رسمت خطًا أسفل مركز أحد هذه التوزيعات، فإن الجانبين الأيسر والأيمن لكل توزيع سيعكسان بعضهما البعض بشكل مثالي.

التوزيعات المتناظرة ونظرية الحد المركزي

إحدى أهم النظريات في جميع الإحصائيات هي نظرية الحد المركزي، والتي تنص على أن توزيع المعاينة لمتوسط العينة يكون طبيعيًا تقريبًا إذا كان حجم العينة كبيرًا بدرجة كافية، حتى لو كان توزيع السكان غير طبيعي .

ومن أجل تطبيق نظرية الحد المركزي، يجب أن يكون حجم العينة كبيرًا بدرجة كافية. لقد اتضح أن العدد الدقيق للأشخاص “الكبار بما يكفي” يعتمد على الشكل الأساسي للتوزيع السكاني.

خصوصاً:

• إذا كان توزيع السكان متماثلا، فإن حجم عينة صغير يصل إلى 15 يكون كافيا في بعض الأحيان.
• إذا كان توزيع السكان منحرفا، عادة ما تكون عينة من 30 شخصا على الأقل ضرورية.
• إذا كان توزيع السكان منحرفا للغاية، فقد يكون من الضروري أخذ عينة من 40 شخصا أو أكثر.

لذا فإن ميزة التوزيعات المتماثلة هي أننا نحتاج إلى أحجام عينات أصغر لتطبيق نظرية الحد المركزي عند حساب فترات الثقة أو إجراءاختبار الفرضيات .

مصادر إضافية

مقدمة لنظرية الحد المركزي
ما هو التوزيع الثنائي؟
دليل للتوزيعات المنحرفة لليسار واليمين