خط الانحدار

By دكتور بنيامين أندرسون زومار 2, 2023 إحصائيات 0 Comments

تشرح هذه المقالة ما هو خط الانحدار في الإحصائيات. لذا، ستجد كيفية حساب خط الانحدار بين متغيرين، وتمرينًا تم حله، بالإضافة إلى آلة حاسبة عبر الإنترنت لحساب خط الانحدار لأي عينة من البيانات.

ما هو خط الانحدار؟

في الإحصاء، خط الانحدار هو الخط الذي يتم الحصول عليه من نموذج الانحدار الخطي البسيط . بتعبير أدق، خط الانحدار هو الخط الذي يناسب المخطط المبعثر، وبالتالي، يصف بشكل أفضل مجموعة من البيانات الإحصائية.

وبالتالي، فإن معادلة خط الانحدار تربط رياضيًا بين المتغير المستقل X والمتغير التابع Y لمجموعة من البيانات. على الرغم من أن خط الانحدار غير قادر عمومًا على تحديد قيمة كل ملاحظة بدقة، إلا أنه يمكن أن يوفر تقديرًا تقريبيًا لقيمتها.

كما ترون في الرسم البياني السابق، يساعدنا خط الانحدار على رؤية اتجاه مجموعة البيانات ونوع العلاقة الموجودة بين المتغير المستقل والمتغير التابع. أدناه سوف ننظر في تطبيقات خط الانحدار.

صيغة خط الانحدار

الآن بعد أن عرفنا تعريف خط الانحدار، دعونا نرى كيفية حساب معادلة خط نموذج الانحدار الخطي.

مثل أي خط، تتكون معادلة خط الانحدار من الثابت (b ₀ ) والميل (b ₁ ):

$y=b_0+b_1x$

وبالتالي، فإن صيغ حساب معاملات خط الانحدار الخطي هي كما يلي:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}$

ذهب:

$b_0$

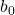
هو ثابت خط الانحدار.
$b_1$

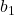
هو ميل خط الانحدار.
$x_i$

هي قيمة المتغير المستقل X للبيانات i.
$y_i$

هي قيمة المتغير التابع Y للبيانات i.
$\overline{x}$

هو متوسط قيم المتغير المستقل
$\overline{y}$

هو متوسط قيم المتغير التابع Y.

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب خط الانحدار لأي مجموعة بيانات.

مثال ملموس لخط الانحدار

لاستكشاف مفهوم خط الانحدار بشكل أكبر، فيما يلي مثال عملي لكيفية إنشاء خط الانحدار.

بعد إجراء اختبار الإحصاء، تم سؤال خمسة طلاب عن عدد ساعات الدراسة التي قضوها في الامتحان، وتظهر البيانات في الجدول أدناه. حساب خط الانحدار من البيانات الإحصائية التي تم جمعها لربط ساعات الدراسة خطيا بالدرجة التي تم الحصول عليها. بعد ذلك، حدد الدرجة التي سيحصل عليها الطالب الذي درس 8 ساعات.

للعثور على خط الانحدار لبيانات العينة، نحتاج إلى تحديد المعاملين b ₀ وb ₁ للمعادلة، وللقيام بذلك، نحتاج إلى استخدام الصيغ الموضحة في القسم أعلاه.

ومع ذلك، لتطبيق الصيغ الخاصة بخط الانحدار الخطي، يجب علينا أولاً حساب متوسط المتغير المستقل ومتوسط المتغير التابع:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

الآن بعد أن عرفنا متوسطات المتغيرات، نحسب المعامل b ₁ للنموذج باستخدام الصيغة المقابلة له:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

وأخيرًا، نحسب المعامل b ₀ للنموذج باستخدام الصيغة المقابلة له:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

وباختصار فإن معادلة خط الانحدار الخطي للمشكلة هي كما يلي:

$y=2,0294+0,4412x$

يمكنك أدناه رؤية التمثيل الرسومي لبيانات العينة بالإضافة إلى الخط المستقيم لنموذج الانحدار الخطي البسيط:

بمجرد قيامنا بحساب خط الانحدار، للتنبؤ بالدرجة التي سيحصل عليها الطالب الذي درس 8 ساعات، ما عليك سوى استبدال هذه القيمة في معادلة خط الانحدار الذي تم الحصول عليه:

$y=2,0294+0,4412\cdot 8=5,56$

وبالتالي، ووفقاً لنموذج الانحدار الخطي الذي تم تنفيذه، إذا درس الطالب لمدة ثماني ساعات، فإنه سيحصل على درجة 5.56 في الامتحان.

ما هو خط الانحدار المستخدم؟

بشكل أساسي، لخط الانحدار استخدامان: يتم استخدام خط الانحدار لتحديد نوع العلاقة الموجودة بين متغيرين، ومن ناحية أخرى، يسمح لك خط الانحدار أيضًا بالتنبؤ بقيمة ملاحظة جديدة.

يخبرنا ميل خط الانحدار بمدى العلاقة بين المتغير المستقل والمتغير التابع. إذا كان الميل موجبًا، فهذا يعني أن المتغير التابع يتناسب طرديًا مع المتغير المستقل، بينما إذا كان الميل سالبًا، فهذا يعني أن المتغيرات متناسبة عكسيًا. وأخيرا، إذا كان معامل الميل قريبا جدا من الصفر، فهذا يعني أن الارتباط بين المتغيرين ضعيف جدا.

بالإضافة إلى ذلك، إذا كانت معادلة خط الانحدار معروفة، فيمكن التنبؤ بقيمة المتغير التابع بقيمة جديدة للمتغير المستقل، كما فعلنا في المثال أعلاه. وبالتالي، كلما تم تكييف خط الانحدار بشكل أفضل، كلما كانت التنبؤات التي يقدمها أفضل.

حاسبة خط الانحدار

أدخل عينة من البيانات في الآلة الحاسبة التالية لحساب خط الانحدار بين المتغيرين. تحتاج إلى فصل أزواج البيانات، بحيث يوجد في المربع الأول فقط قيم المتغير المستقل X وفي المربع الثاني يوجد فقط قيم المتغير التابع Y.

يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر