شبه الانحراف المعياري

By دكتور بنيامين أندرسون زومار 3, 2023 إحصائيات 0 Comments

تشرح هذه المقالة ما هو الانحراف شبه المعياري في الإحصائيات وكيفية حسابه. لذلك ستجد صيغة الانحراف شبه المعياري، وتمرينًا تم حله، بالإضافة إلى آلة حاسبة عبر الإنترنت لحساب الانحراف شبه المعياري لأي مجموعة بيانات.

ما هو الانحراف شبه المعياري؟

في الإحصاء، الانحراف شبه المعياري هو مقياس للتشتت يشير إلى تباين العينة. على وجه التحديد، الانحراف شبه المعياري يساوي الجذر التربيعي لمجموع مربعات الانحرافات مقسومًا على إجمالي عدد نقاط البيانات ناقص واحد.

رمز الانحراف شبه المعياري هو σ _n-1 os _n-1 .

قد يُطلق على الانحراف شبه المعياري أيضًا اسم الانحراف شبه المعياري ، ويسمى أيضًا أحيانًا الانحراف المعياري للعينة، لأنه يتم حسابه عادةً باستخدام قيم من عينة إحصائية. أدناه سوف نتناول بالتفصيل الفرق بين الانحراف شبه المعياري والانحراف المعياري.

صيغة الانحراف شبه المعياري

الانحراف شبه المعياري يساوي الجذر التربيعي لمجموع مربعات انحرافات سلسلة البيانات مقسومًا على إجمالي عدد الملاحظات ناقص واحد. ولذلك فإن صيغة حساب الانحراف شبه المعياري هي:

ذهب:

$\sigma_{n-1}$

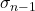
وهذا هو الانحراف شبه المعياري.
$x_i$

هي قيمة البيانات

$i$

.
$n$

هو العدد الإجمالي للبيانات.
$\overline{x}$

هو متوسط مجموعة البيانات.

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب الانحراف شبه المعياري لأي مجموعة بيانات.

مثال لحساب الانحراف شبه المعياري

وبالنظر إلى تعريف الانحراف شبه المعياري، يمكنك أدناه رؤية مثال بسيط لكيفية حساب الانحراف شبه المعياري لمجموعة بيانات.

تعتبر ميزانية الشركة المخصصة لقسم البحث والتطوير متقلبة للغاية، لأنها تعتمد على الربح الاقتصادي الذي حصلت عليه الشركة في العام السابق. وبذلك كانت ميزانية هذا الباب خلال السنوات الخمس الماضية: 3، 6، 2، 9، 4 ملايين يورو. احسب الانحراف شبه المعياري لسلسلة البيانات هذه.

أول شيء يتعين علينا القيام به لتحديد الانحراف شبه المعياري هو حساب الوسط الحسابي للعينة. للقيام بذلك، نقوم بجمع كافة البيانات وتقسيمها على إجمالي عدد الملاحظات، وهو خمسة:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

بعد ذلك، نطبق صيغة الانحراف شبه المعياري:

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

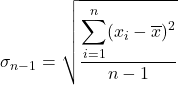
نعوض البيانات في الصيغة:

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

وأخيرا نحسب الانحراف شبه المعياري:

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

وباختصار فإن الانحراف شبه المعياري لعينة البيانات هو 2.77 مليون.

➤ انظر: شبه التباين

حاسبة الانحراف شبه المعياري

أدخل مجموعة بيانات إحصائية في الآلة الحاسبة الموجودة على الإنترنت أدناه لحساب انحرافها شبه المعياري. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.

الانحراف شبه المعياري والانحراف المعياري

أخيرًا، سنرى ما هو الفرق بين الانحراف شبه المعياري والانحراف المعياري، حيث أنهما مقياسان إحصائيان مختلفان لهما اسم مشابه جدًا ويتم حسابهما بطريقة مشابهة جدًا.

الفرق بين الانحراف شبه المعياري والانحراف المعياري هو مقام الصيغة. لحساب الانحراف شبه المعياري، يتم القسمة على n-1، ولكن يتم حساب الانحراف المعياري عن طريق القسمة على n.

ولذلك، فإن الانحراف شبه المعياري والانحراف المعياري مرتبطان رياضيا، حيث أن الانحراف شبه المعياري يعادل الانحراف المعياري مضروبًا في الجذر التربيعي لـ n (إجمالي عدد نقاط البيانات) على n-1.

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

ومن المعادلة السابقة يمكننا أن نستنتج أنه بالنسبة لنفس مجموعة البيانات، فإن قيمة الانحراف شبه المعياري ستكون دائما أكبر من قيمة الانحراف المعياري.

بالإضافة إلى ذلك، غالبًا ما تُستخدم صيغة الانحراف شبه المعياري لحساب الانحراف المعياري للعينة لأنها تزيل التحيز. وبالتالي فإن الانحراف شبه المعياري يعد مقدرًا جيدًا للانحراف المعياري للسكان. ولهذا السبب، عند إجراء استنتاج إحصائي من عينة، من الشائع جدًا القول بأن الانحراف المعياري يتم حسابه بينما في الواقع، يتم حساب الانحراف شبه المعياري.

➤ انظر: خصائص الانحراف المعياري

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر