كيفية استخدام طريقة الكوع في بايثون للعثور على المجموعات المثلى

تُعرف إحدى خوارزميات التجميع الأكثر شيوعًا في التعلم الآلي باسم التجميع بوسائل k .

إن تجميع وسائل K هو أسلوب نضع فيه كل ملاحظة من مجموعة بيانات في إحدى مجموعات K.

الهدف النهائي هو الحصول على مجموعات K حيث تكون الملاحظات داخل كل مجموعة متشابهة تمامًا مع بعضها البعض بينما تختلف الملاحظات في المجموعات المختلفة تمامًا عن بعضها البعض.

عند القيام بالتجميع باستخدام k، فإن الخطوة الأولى هي اختيار قيمة لـ K – عدد المجموعات التي نريد وضع الملاحظات فيها.

تُعرف إحدى الطرق الأكثر شيوعًا لاختيار قيمة لـ K بطريقة الكوع ، والتي تتضمن إنشاء مخطط بعدد المجموعات على المحور x والإجمالي في مجموع المربعات على المحور y، ثم تحديد حيث تظهر “الركبة” أو المنعطف في المؤامرة.

تخبرنا النقطة الموجودة على المحور السيني حيث تحدث “الركبة” بالعدد الأمثل للمجموعات التي سيتم استخدامها في خوارزمية التجميع بالوسائل k.

يوضح المثال التالي كيفية استخدام طريقة الكوع في بايثون.

الخطوة 1: استيراد الوحدات الضرورية

أولاً، سوف نقوم باستيراد كافة الوحدات التي سنحتاجها لإجراء تجميع الوسائل k:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

الخطوة 2: إنشاء DataFrame

بعد ذلك، سنقوم بإنشاء DataFrame يحتوي على ثلاثة متغيرات لـ 20 لاعبًا مختلفًا لكرة السلة:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

الخطوة 3: استخدم طريقة الكوع للعثور على العدد الأمثل للمجموعات

لنفترض أننا نريد استخدام مجموعات k-means لتجميع الجهات الفاعلة المتشابهة معًا بناءً على هذه المقاييس الثلاثة.

لتنفيذ تجميع الوسائل k في بايثون، يمكننا استخدام دالة KMeans من وحدة sklearn .

الوسيط الأكثر أهمية لهذه الدالة هو n_clusters ، الذي يحدد عدد المجموعات التي سيتم وضع الملاحظات فيها.

لتحديد العدد الأمثل للمجموعات، سنقوم بإنشاء رسم بياني يعرض عدد المجموعات بالإضافة إلى SSE (مجموع الأخطاء المربعة) للنموذج.

سنبحث بعد ذلك عن “الركبة” حيث يبدأ مجموع المربعات في “الانحناء” أو الاستقرار. تمثل هذه النقطة العدد الأمثل للمجموعات.

يوضح التعليمة البرمجية التالية كيفية إنشاء هذا النوع من المخطط الذي يعرض عدد المجموعات على المحور السيني وSSE على المحور الصادي:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

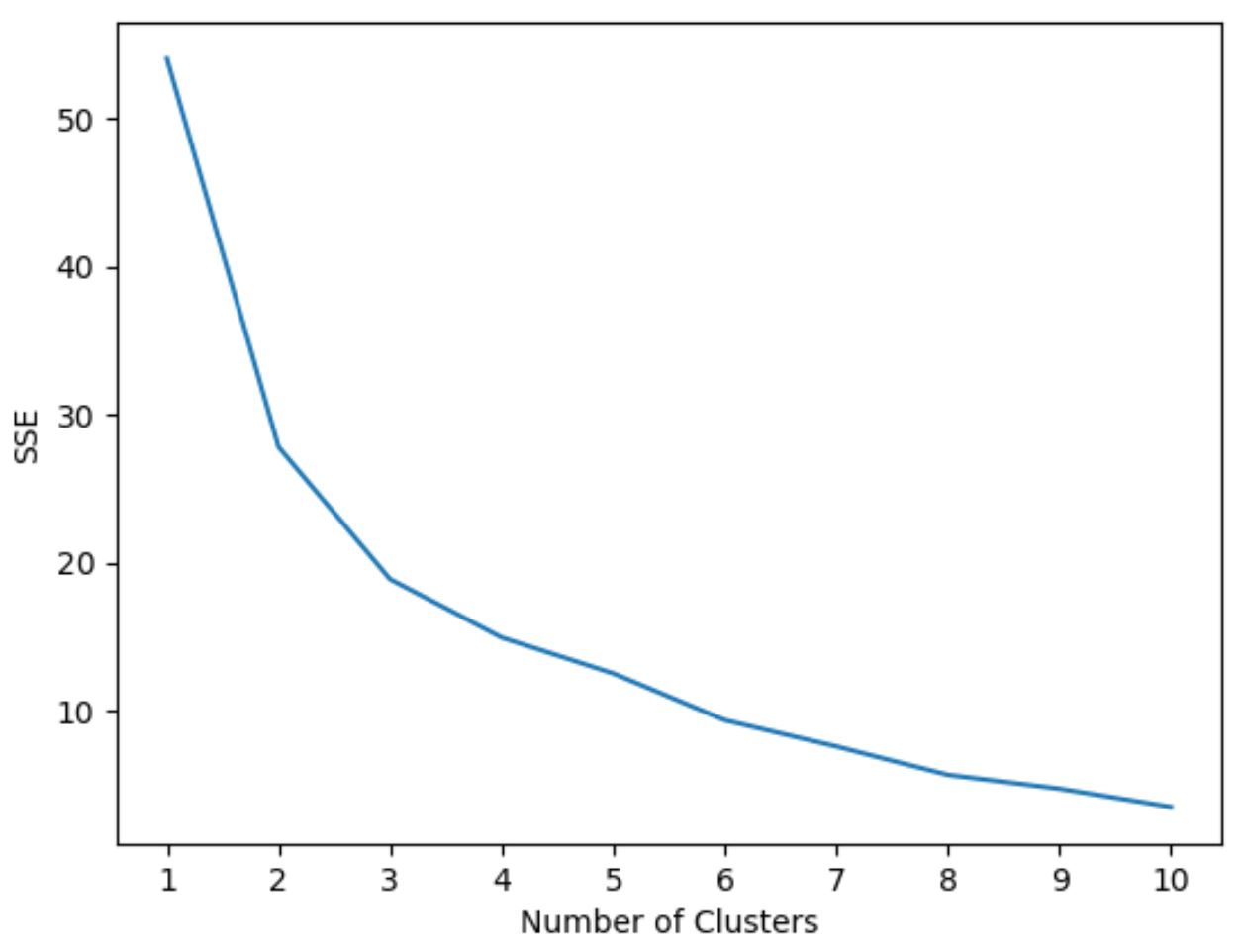
في هذا الرسم البياني، يبدو أن هناك شبك أو “ركبة” عند k = 3 مجموعات .

لذلك، سوف نستخدم 3 مجموعات عند ملاءمة نموذج التجميع الخاص بنا في الخطوة التالية.

الخطوة 4: تنفيذ مجموعة K-Means باستخدام Optimal K

يوضح التعليمة البرمجية التالية كيفية إجراء التجميع على مجموعة البيانات باستخدام القيمة المثلى لـ k لـ 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

يعرض الجدول الناتج تعيينات المجموعة لكل ملاحظة في DataFrame.

لتسهيل تفسير هذه النتائج، يمكننا إضافة عمود إلى DataFrame يوضح مهمة المجموعة لكل لاعب:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

يحتوي عمود المجموعة على رقم المجموعة (0، 1، أو 2) الذي تم تعيينه لكل لاعب.

اللاعبون الذين ينتمون إلى نفس المجموعة لديهم قيم متشابهة تقريبًا لأعمدة النقاط والتمريرات الحاسمة والمرتدات .

ملاحظة : يمكنك العثور على الوثائق الكاملة لوظيفة KMeans الخاصة بـ sklearn هنا .

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في بايثون:

كيفية تنفيذ الانحدار الخطي في بايثون
كيفية تنفيذ الانحدار اللوجستي في بايثون
كيفية إجراء التحقق من صحة K-Fold في بايثون