قاعدة الإضافة (أو قاعدة الإضافة)

By دكتور بنيامين أندرسون زومار 1, 2023 احتمالا 0 Comments

تشرح هذه المقالة ما هي قاعدة الجمع، والمعروفة أيضًا بقاعدة الجمع، وما يتم استخدامها في الاحتمالات والإحصاء. بالإضافة إلى ذلك، ستتمكن من رؤية صيغة قاعدة الجمع وحل التمارين التي توضح كيفية استخدامها.

ما هي قاعدة الإضافة (أو قاعدة الإضافة)؟

تنص قاعدة الجمع (أو قاعدة الإضافة ) على أن مجموع احتمالات حدثين يساوي مجموع احتمال وقوع كل حدث على حدة مطروحًا منه احتمال وقوع الحدثين في نفس الوقت.

ولذلك، فإن صيغة قاعدة الجمع هي P(A⋃B)=P(A)+P(B)−P(A⋂B).

وبالتالي، لجمع احتمالين، لا يمكننا ببساطة جمع كل احتمال، حيث يجب علينا أيضًا طرح الحد الذي يمثل الاحتمال المشترك للحدثين. ومع ذلك، في بعض الحالات، فقط عن طريق إضافة احتمال كل حدث يمكننا الحصول على النتيجة الصحيحة لمجموع الاحتمالات. وفيما يلي سنرى ما هي هذه الحالات.

باختصار، يتم استخدام قاعدة الجمع لحساب احتمال وقوع حدث أو آخر، أي احتمال وقوع حدث واحد على الأقل من حدثين محتملين.

صيغة قاعدة الإضافة

تنص قاعدة الجمع على أنه لحساب احتمال وقوع الحدث A أو الحدث B، يجب علينا جمع احتمال وقوع الحدث A بالإضافة إلى احتمال وقوع الحدث B وطرح احتمال وقوع كلا الحدثين في نفس الوقت. .

وبالتالي فإن صيغة قاعدة الإضافة (أو قاعدة الإضافة) هي كما يلي:

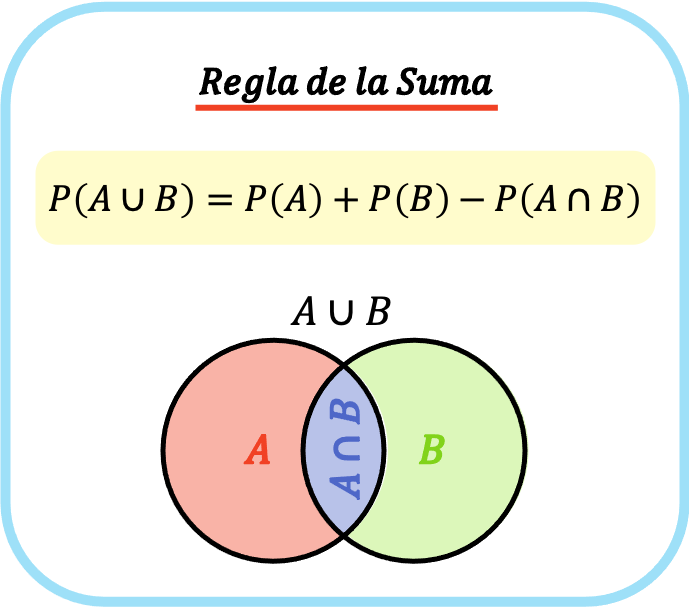
ذهب:

$P(A\cup B)$

هو احتمال الحدث A أو الحدث B.
$P(A)$

هو احتمال وقوع الحدث A.
$P(B)$

هو احتمال وقوع الحدث B.
$P(A\cap B)$

هو الاحتمال المشترك لوقوع الحدث A والحدث B.

لذلك، لاستخدام قاعدة المجموع، تحتاج إلى معرفة كيفية حساب الاحتمال المشترك لحدثين. ويمكنك أن ترى كيف يتم ذلك في الرابط التالي:

➤ انظر: كيفية حساب الاحتمال المشترك

قاعدة مجموع الأمثلة للأحداث الحصرية

لإنهاء فهم المفهوم، دعونا نرى مثالاً لكيفية تطبيق قاعدة الجمع.

نضع 10 كرات زرقاء و6 كرات برتقالية و4 كرات خضراء في صندوق. ما احتمال سحب كرة زرقاء أو برتقالية؟

يطلب منا التمرين تحديد احتمال وقوع حدث أو آخر. لذلك، لحل المشكلة، نحتاج إلى استخدام صيغة قاعدة الجمع:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

لذلك، نقوم أولاً بحساب احتمال وقوع كل حدث على حدة باستخدام قاعدة لابلاس :

$P(\text{bola azul})=\cfrac{10}{10+6+4}=0,5$

$P(\text{bola naranja})=\cfrac{6}{10+6+4}=0,3$

ومع ذلك، في هذه الحالة، لا يمكن للحدثين أن يقعا في نفس الوقت، لأنهما حدثان متنافيان . لذا، إذا رسمنا كرة زرقاء، فلن نتمكن من رسم كرة برتقالية، والعكس صحيح.

ولذلك، فإن الاحتمال المشترك لكلا الحدثين هو صفر، وبالتالي يتم تبسيط صيغة قاعدة المجموع:

$P(A\cup B)=P(A)+P(B)-\cancelto{0}{P(A\cap B)}$

إذن حساب احتمال الإمساك بالكرة الزرقاء أو البرتقالية هو كما يلي:

$\begin{aligned}P(\text{bola azul}\cup \text{bola naranja})&=P(\text{bola azul})+P(\text{bola azul})\\[2ex]&=0,5+0,3\\[2ex]&=0,8\end{aligned}$

باختصار، احتمال سحب كرة زرقاء أو برتقالية من الصندوق هو 80%.

مثال على قاعدة الإلحاق للأحداث غير الحصرية

بعد أن رأينا مثالاً ملموسًا لقاعدة الجمع عندما تكون الأحداث غير حصرية، سنرى الآن كيف يتم استخدام هذا القانون عندما تكون الأحداث غير حصرية.

إذا رمينا قطعة نقود مرتين، فما احتمال ظهور الصورة عند رميتها مرة واحدة على الأقل؟

في هذه الحالة، الأحداث ليست متنافية، إذ يمكننا الحصول على “رأس” في الرمية الأولى و”ذيول” في الرمية الثانية. وبالتالي فإن صيغة قاعدة الجمع ليست مبسطة وهي كما يلي:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

لذا، نحتاج أولاً إلى حساب احتمال الحصول على “صورة” عند رمي العملة المعدنية من خلال تطبيق قاعدة لابلاس:

$P(\text{cara})=\cfrac{1}{2}=0,5$

بالإضافة إلى ذلك، فإن الحدثين مستقلان، لذا يمكننا حساب الاحتمال المشترك للحدثين باستخدام قاعدة الضرب :

$P(\text{cara}\cap \text{cara})=\cfrac{1}{2}\cdot \cfrac{1}{2}=0,5\cdot 0,5=0,25$

أخيرًا، للعثور على احتمال سقوط الرؤوس في إحدى الرميتين على الأقل، ما عليك سوى استبدال القيم في صيغة قاعدة الجمع وإجراء الحساب:

$\begin{aligned}P(\text{cara}\cup \text{cara})&=P(\text{cara})+P(\text{cara})-P(\text{cara}\cap \text{cara})\\[2ex]&=0,5+0,5-0,25\\[2ex]&=0,75\end{aligned}$

في الختام، فإن احتمال ظهور صورة مرة واحدة على الأقل من خلال رمي قطعة نقود مرتين هو 75%.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر