توزيع باريتو
تشرح هذه المقالة ما هو توزيع باريتو في الإحصائيات وفيم يُستخدم. ستتمكن أيضًا من رؤية الرسم البياني لتوزيع باريتو وخصائص هذا النوع من التوزيع الاحتمالي.
ما هو توزيع باريتو؟
توزيع باريتو هو توزيع احتمالي مستمر يستخدم في الإحصاء لنمذجة مبدأ باريتو. ولذلك فإن توزيع باريتو هو توزيع احتمالي له قيم قليلة يكون احتمال حدوثها أعلى بكثير من باقي القيم.
تذكر أن قانون باريتو، والذي يُطلق عليه أيضًا قاعدة 80-20، هو مبدأ إحصائي يقول أن معظم أسباب الظاهرة يرجع إلى جزء صغير من السكان.
يحتوي توزيع باريتو على معلمتين مميزتين: معلمة المقياس x m ومعلمة الشكل α.
![]()
في الأصل، تم استخدام توزيع باريتو لوصف توزيع الثروة بين السكان، لأن معظمها كان بسبب نسبة صغيرة من السكان. لكن توزيع باريتو حاليًا له العديد من التطبيقات، على سبيل المثال في مراقبة الجودة، في الاقتصاد، في العلوم، في المجال الاجتماعي، وما إلى ذلك.
تم تسمية توزيع باريتو على اسم الاقتصادي فيلفريدو باريتو، الذي صاغ التوزيع. ومع ذلك، فقد اشتهر بمخطط باريتو.
جدول توزيع باريتو
الآن بعد أن عرفنا تعريف توزيع باريتو، دعونا نلقي نظرة على عدة أمثلة لتوزيعات باريتو ممثلة بيانيا.
لذا، يمكنك أدناه رؤية كيف يبدو الرسم البياني لدالة الكثافة لتوزيع باريتو اعتمادًا على قيمها المميزة:
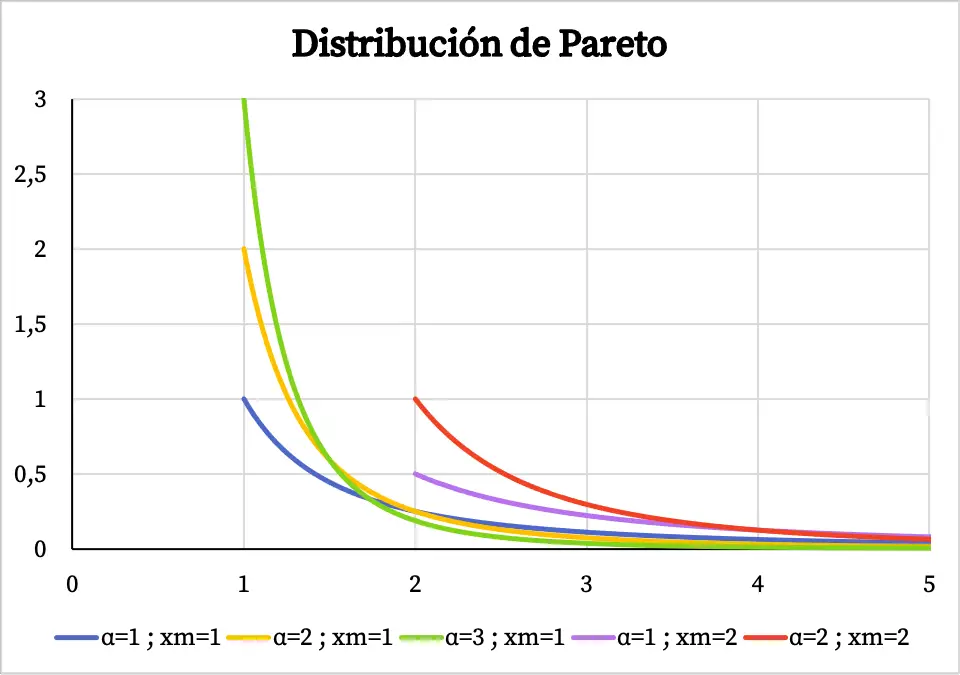
لاحظ أن مجال توزيع باريتو ينتقل من القيمة x m إلى +∞، ولهذا السبب لا توجد دالة الكثافة قبل قيمة x m .
من ناحية أخرى، فإن الرسم البياني لدالة الاحتمالية التراكمية لتوزيع باريتو هو كما يلي:
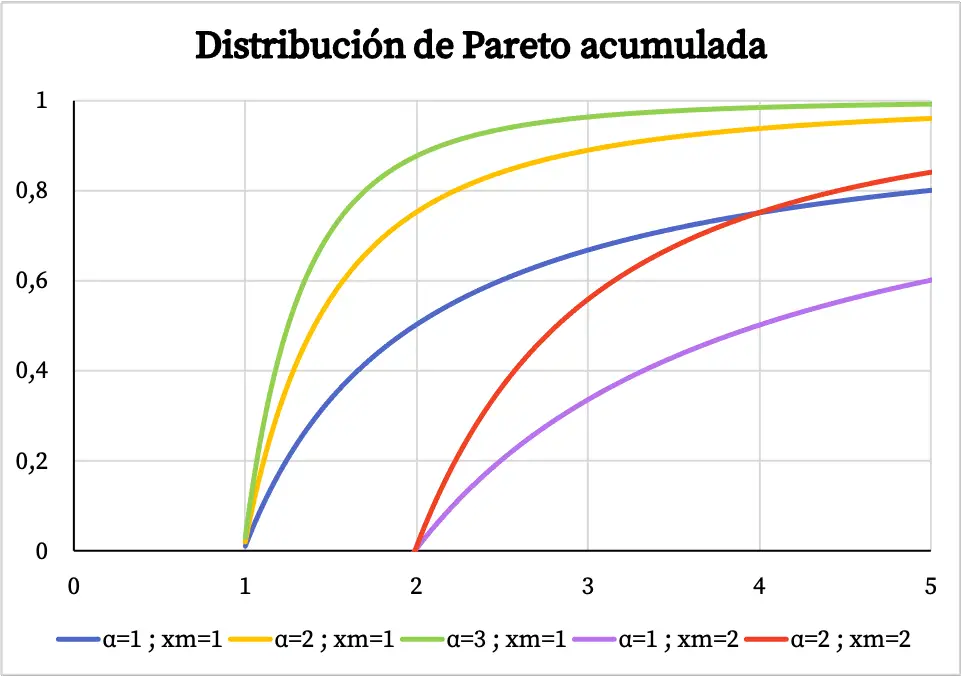
خصائص توزيع باريتو
وفيما يلي أهم خصائص توزيع باريتو المتعلقة بنظرية الاحتمالات والإحصاء.
- يحتوي توزيع باريتو على معلمتين مميزتين تحددان منحنىه: معلمة المقياس x m ومعلمة الشكل α.
![]()
- يتكون مجال توزيع باريتو من جميع الأعداد الحقيقية من معلمة المقياس إلى زائد اللانهاية.
![]()
- إذا كانت α أكبر من 1، فإن متوسط توزيع باريتو يساوي حاصل ضرب α في x m و α ناقص 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
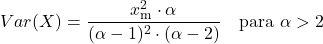
![]()
- نمط توزيع باريتو يعادل معلمة المقياس x m للتوزيع.
![]()
- صيغة دالة الكثافة لتوزيع باريتو هي:
![]()
- وبالمثل، فإن صيغة دالة الاحتمال التراكمي لتوزيع باريتو هي:
![]()
- يعتمد معامل عدم التماثل لتوزيع باريتو فقط على معلمة الشكل α والتعبير عنها هو:
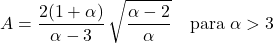
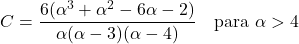
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر