ما هو y hat في الإحصائيات؟

في الإحصاء، المصطلح y hat (مكتوب ŷ ) يشير إلى القيمة المقدرة لمتغير الاستجابة في نموذج الانحدار الخطي .

نكتب بشكل عام معادلة الانحدار المقدرة على النحو التالي:

ŷ = β ₀ + β ₁ س

ذهب:

• ŷ : القيمة المقدرة لمتغير الاستجابة
• β ₀ : القيمة المتوسطة لمتغير الاستجابة عندما يكون المتغير المتوقع صفراً
• β ₁ : متوسط التغير في متغير الاستجابة المرتبط بزيادة وحدة واحدة في المتغير التنبئي

على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية التي توضح عدد الساعات التي درسها ستة طلاب مختلفين بالإضافة إلى درجات الامتحانات النهائية:

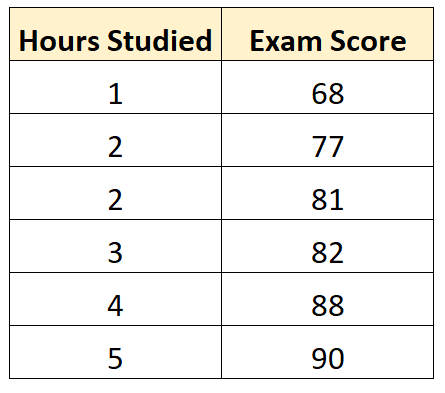
لنفترض أننا نستخدم برامج إحصائية (مثل R أو Excel أو Python أو حتى يدويًا) لتناسب نموذج الانحدار التالي باستخدام ساعات الدراسة كمتغير متوقع ونتائج الامتحان كمتغير الاستجابة:

النتيجة = 66.615 + 5.0769*(ساعات)

أما طريقة تفسير معاملات الانحدار في هذا النموذج فهي كما يلي:

• متوسط درجة الامتحان للطالب الذي يدرس صفر ساعة هو 66,615 .
• وتزداد درجة الامتحان بمعدل 5.0769 نقطة لكل ساعة إضافية مدروسة.

يمكننا استخدام معادلة الانحدار هذه لتقدير درجة طالب معين بناءً على عدد الساعات المدروسة.

على سبيل المثال، الطالب الذي يدرس لمدة 3 ساعات يجب أن يحصل على درجة:

النتيجة = 66.615 + 5.0769*(3) = 81.85

لماذا يتم استخدام قبعة Y؟

يُستخدم رمز “القبعة” في الإحصائيات للإشارة إلى أي مصطلح “مقدر”. على سبيل المثال، يتم استخدام ŷ للدلالة على متغير الاستجابة المقدرة.

عادةً، عندما نلائم نماذج الانحدار الخطي، فإننا نستخدم عينة من البيانات من مجتمع ما، لأن هذا أكثر ملاءمة وأقل استهلاكًا للوقت من جمع البيانات لكل ملاحظة محتملة في مجتمع ما.

لذلك عندما نجد معادلة الانحدار، فإننا نقدر فقط العلاقة الحقيقية بين متغير متنبئ ومتغير استجابة.

ولهذا السبب نستخدم المصطلح ŷ في معادلة الانحدار بدلاً من y.

مصادر إضافية

مقدمة إلى الانحدار الخطي البسيط
مقدمة في الانحدار الخطي المتعدد
مقدمة للمتغيرات التفسيرية والاستجابة