كيفية تفسير الجذر التربيعي للخطأ (rmse)

تحليل الانحدار هو أسلوب يمكننا استخدامه لفهم العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .

إحدى طرق تقييم مدى ملاءمة نموذج الانحدار لمجموعة بيانات هي حساب متوسط الخطأ المربع ، وهو مقياس يخبرنا بمتوسط المسافة بين القيم المتوقعة للنموذج والقيم الفعلية لمجموعة البيانات.

كلما انخفض RMSE، كلما كان النموذج المعطى قادرًا على “ملاءمة” مجموعة البيانات بشكل أفضل.

صيغة العثور على متوسط مربع الخطأ، والتي غالبًا ما يتم اختصارها بـ RMSE ، هي:

RMSE = √ Σ(P _i – O _i ) ² / n

ذهب:

• Σ هو رمز خيالي يعني “المجموع”
• P _i هي القيمة المتوقعة للملاحظة ⁱ في مجموعة البيانات
• O _i هي القيمة المرصودة للملاحظة ^رقم في مجموعة البيانات
• n هو حجم العينة

يوضح المثال التالي كيفية تفسير RMSE لنموذج انحدار محدد.

مثال: كيفية تفسير RMSE لنموذج الانحدار

لنفترض أننا نريد بناء نموذج انحدار يستخدم “ساعات الدراسة” للتنبؤ “بدرجة الامتحان” للطلاب في امتحان دخول جامعي معين.

نقوم بجمع البيانات التالية لـ 15 طالبًا:

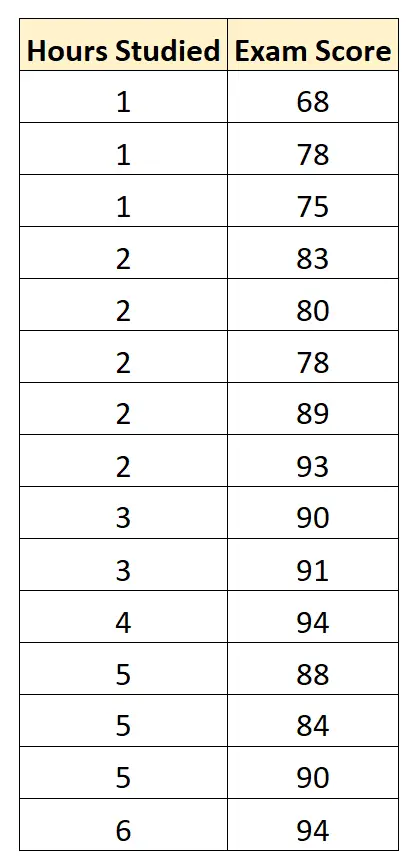
نستخدم بعد ذلك البرامج الإحصائية (مثل Excel وSPSS وR وPython) وما إلى ذلك. للعثور على نموذج الانحدار المناسب التالي:

درجة الامتحان = 75.95 + 3.08* (ساعات الدراسة)

يمكننا بعد ذلك استخدام هذه المعادلة للتنبؤ بدرجة امتحان كل طالب، بناءً على عدد الساعات التي درسها:

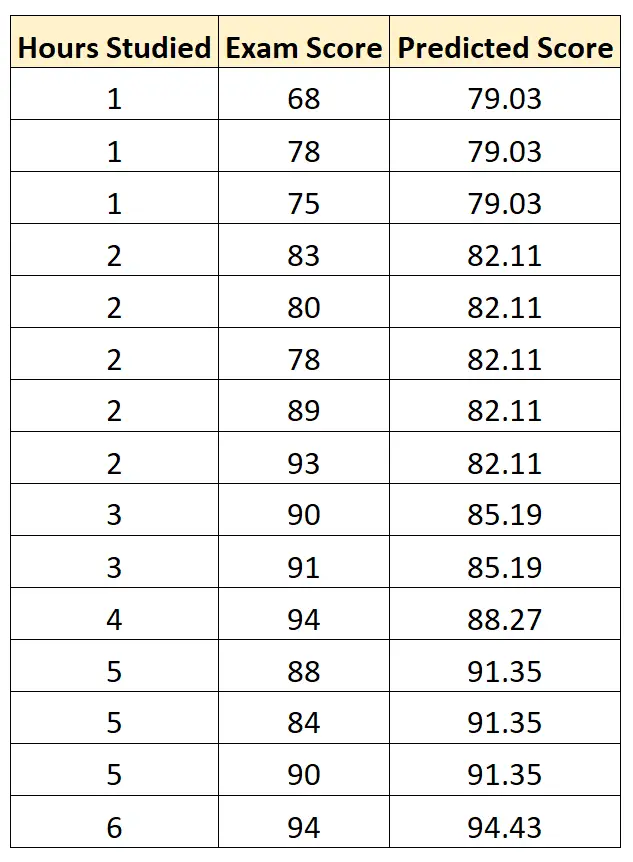
يمكننا بعد ذلك حساب الفرق التربيعي بين كل درجة اختبار متوقعة ودرجة الاختبار الفعلية. يمكننا بعد ذلك أن نأخذ الجذر التربيعي لمتوسط هذه الاختلافات:

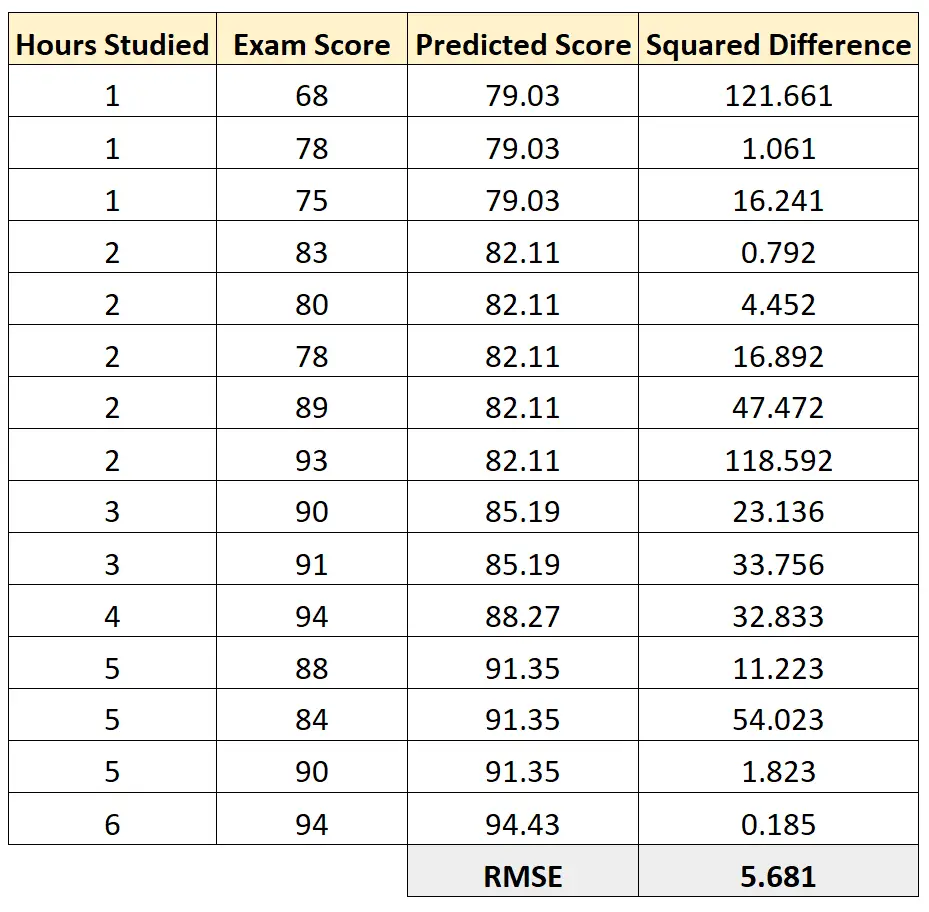
تبين أن RMSE لنموذج الانحدار هذا هو 5.681 .

تذكر أن بقايا نموذج الانحدار هي الاختلافات بين قيم البيانات المرصودة والقيم المتوقعة للنموذج.

المتبقي = (P _i – O _i )

ذهب

• P _i هي القيمة المتوقعة للملاحظة ⁱ في مجموعة البيانات
• O _i هي القيمة المرصودة للملاحظة ^رقم في مجموعة البيانات

وتذكر أن RMSE لنموذج الانحدار يتم حسابه على النحو التالي:

RMSE = √ Σ(P _i – O _i ) ² / n

وهذا يعني أن RMSE يمثل الجذر التربيعي لتباين القيم المتبقية.

وهذه قيمة مفيدة يجب معرفتها لأنها تعطينا فكرة عن متوسط المسافة بين قيم البيانات المرصودة وقيم البيانات المتوقعة.

يتناقض هذا مع R-squared للنموذج، والذي يخبرنا عن مقدار التباين في متغير الاستجابة الذي يمكن تفسيره بواسطة متغير (متغيرات) التوقع للنموذج.

مقارنة قيم RMSE للنماذج المختلفة

يعد RMSE مفيدًا بشكل خاص لمقارنة ملاءمة نماذج الانحدار المختلفة.

على سبيل المثال، لنفترض أننا نريد بناء نموذج انحدار للتنبؤ بدرجات امتحانات الطلاب ونريد العثور على أفضل نموذج ممكن من بين عدة نماذج محتملة.

لنفترض أننا نلائم ثلاثة نماذج انحدار مختلفة ونجد قيم RMSE المقابلة لها:

• RMSE للنموذج 1: 14.5
• RMSE للنموذج 2: 16.7
• RMSE للنموذج 3: 9.8

يحتوي النموذج 3 على أقل RMSE، مما يخبرنا أنه قادر على ملاءمة مجموعة البيانات بشكل أفضل بين النماذج الثلاثة المحتملة.

مصادر إضافية

حاسبة RMSE
كيفية حساب RMSE في إكسل
كيفية حساب RMSE في R
كيفية حساب RMSE في بايثون