كيفية قراءة جدول توزيع مربع كاي
يشرح هذا البرنامج التعليمي كيفية قراءة وتفسير مخطط توزيع مربع كاي.
ما هو جدول توزيع مربع تشي؟
جدول توزيع مربع كاي هو جدول يوضح القيم الحرجة لتوزيع مربع كاي. لاستخدام جدول توزيع مربع كاي، ما عليك سوى معرفة قيمتين:
- درجات الحرية لاختبار مربع كاي
- مستوى ألفا للاختبار (الخيارات الشائعة هي 0.01 و0.05 و0.10)
الصورة التالية توضح أول 20 صفًا من جدول توزيع مربع كاي، مع درجات الحرية على الجانب الأيسر من الجدول ومستويات ألفا في أعلى الجدول:
ملحوظة: يمكنك العثور على جدول توزيع مربع كاي الكامل بدرجات حرية أكبر هنا.
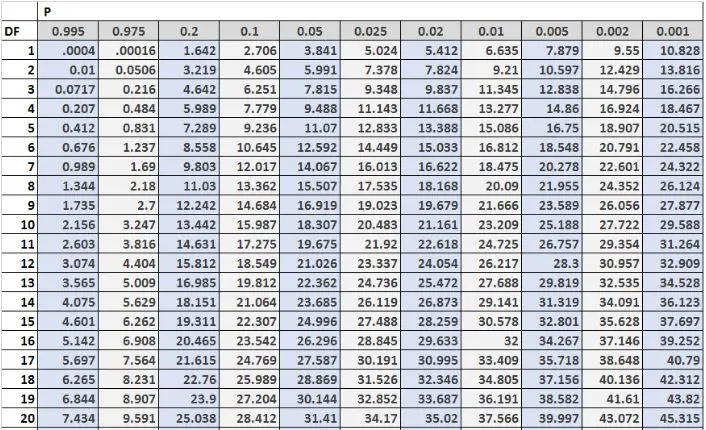
غالبًا ما تتم مقارنة القيم الحرجة في الجدول بإحصائيات اختبار مربع كاي. إذا كانت إحصائية الاختبار أكبر من القيمة الحرجة الموجودة في الجدول، فيمكنك رفض الفرضية الصفرية لاختبار مربع كاي واستنتاج أن نتائج الاختبار ذات دلالة إحصائية.
أمثلة على استخدام جدول توزيع مربع كاي
وسوف نوضح كيفية استخدام جدول توزيع مربع كاي مع الأنواع الثلاثة التالية من اختبارات مربع كاي:
- اختبار مربع كاي للاستقلالية
- اختبار مربع كاي لصلاحية التوافق
- اختبار مربع كاي للتجانس
اختبار مربع كاي للاستقلالية
نحن نستخدم اختبار Chi-square للاستقلال عندما نريد اختبار ما إذا كان هناك ارتباط كبير بين متغيرين فئويين أم لا.
مثال: لنفترض أننا نريد معرفة ما إذا كان الجنس مرتبطًا بتفضيل حزب سياسي أم لا. أخذنا عينة عشوائية بسيطة من 500 ناخب وسألناهم عن تفضيلاتهم الحزبية. وباستخدام مستوى دلالة 0.05، أجرينا اختبار مربع كاي لتحديد ما إذا كان الجنس مرتبطًا بتفضيل الحزب السياسي. ويعرض الجدول التالي نتائج الاستطلاع:
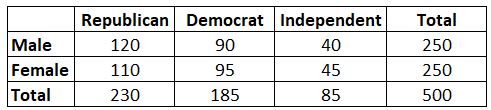
وتبين أن إحصائية الاختبار لاختبار مربع كاي هي 0.864.
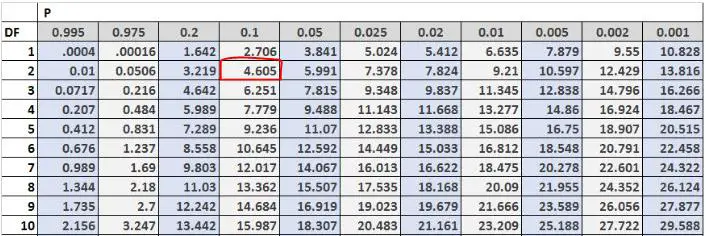
ثم يمكننا إيجاد قيمة الاختبار الحرجة في جدول توزيع مربع كاي. درجات الحرية تساوي (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 وأخبرتنا المشكلة أنه يجب علينا استخدام مستوى ألفا قدره 0.05، وفقا لجدول توزيع مربع كاي، فإن القيمة الحرجة للاختبار هي 5.991 .

وبما أن إحصائية الاختبار لدينا أقل من القيمة الحرجة، فإننا نفشل في رفض فرضية العدم. وهذا يعني أنه ليس لدينا أدلة كافية للقول بوجود علاقة بين النوع الاجتماعي وتفضيلات الأحزاب السياسية.
اختبار مربع كاي لصلاحية التوافق
نحن نستخدم اختبار جودة الملاءمة لمربع كاي عندما نريد اختبار ما إذا كان المتغير القاطع يتبع توزيعًا افتراضيًا أم لا.
مثال: يقول صاحب متجر أن 30% من جميع عملائه في عطلة نهاية الأسبوع يأتون يوم الجمعة، و50% يوم السبت، و20% يوم الأحد. قام باحث مستقل بزيارة المتجر في عطلة نهاية أسبوع عشوائية ووجد 91 عميلاً يوم الجمعة، و104 يوم السبت، و65 يوم الأحد. باستخدام مستوى دلالة 0.10، نقوم بإجراء اختبار مربع كاي للتحقق من جودة الملاءمة لتحديد ما إذا كانت البيانات متوافقة مع ادعاء مالك المتجر.
في هذه الحالة، تبين أن إحصائية الاختبار هي 10616.
ثم يمكننا إيجاد قيمة الاختبار الحرجة في جدول توزيع مربع كاي. درجات الحرية تساوي (#outcomes-1) = 3-1 = 2 والمشكلة تخبرنا أنه يجب علينا استخدام مستوى ألفا قدره 0.10. لذا، وفقًا لجدول توزيع مربع كاي، فإن القيمة الحرجة للاختبار هي 4.605 .
وبما أن إحصائية الاختبار لدينا أكبر من القيمة الحرجة لدينا، فإننا نرفض فرضية العدم. وهذا يعني أن لدينا ما يكفي من الأدلة لنقول إن التوزيع الحقيقي للعملاء الذين يأتون إلى هذا المتجر في عطلة نهاية الأسبوع لا يساوي 30% يوم الجمعة، و50% يوم السبت، و20% يوم الأحد.
اختبار مربع كاي للتجانس
نحن نستخدم اختبار مربع كاي للتجانس عندما نريد إجراء اختبار رسمي لمعرفة ما إذا كان هناك اختلاف في النسب بين مجموعات متعددة أم لا.
مثال: يريد مركز تدريب كرة السلة معرفة ما إذا كان برنامجان تدريبيان جديدان يعملان على تحسين نسبة لاعبيه الذين يجتازون اختبارًا صعبًا في التصويب. تم تعيين 172 لاعبًا بشكل عشوائي للبرنامج 1، و173 لاعبًا للبرنامج 2، و215 لاعبًا للبرنامج الحالي. بعد استخدام البرامج التدريبية لمدة شهر، يقوم اللاعبون بعد ذلك بإجراء اختبار التصويب. الجدول أدناه يوضح عدد اللاعبين الذين اجتازوا اختبار التصويب حسب البرنامج الذي استخدموه.

وباستخدام مستوى دلالة 0.05، قمنا بإجراء اختبار مربع كاي لتحديد ما إذا كان معدل النجاح هو نفسه لكل برنامج تدريبي.
وتبين أن إحصائية الاختبار لاختبار مربع كاي هي 4.208.
ثم يمكننا إيجاد قيمة الاختبار الحرجة في جدول توزيع مربع كاي. درجات الحرية تساوي (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 وأخبرتنا المشكلة أنه يجب علينا استخدام مستوى ألفا قدره 0.05، وفقا لجدول توزيع مربع كاي، فإن القيمة الحرجة للاختبار هي 5.991 .

وبما أن إحصائية الاختبار لدينا أقل من القيمة الحرجة، فإننا نفشل في رفض فرضية العدم. وهذا يعني أنه ليس لدينا أدلة كافية للقول بأن البرامج التدريبية الثلاثة تؤدي إلى نتائج مختلفة.