ماذا يعني إذا كانت الإحصائية مرنة؟

ويقال إن الإحصائية مرنة إذا لم تكن حساسة للقيم المتطرفة.

فيما يلي مثالان للإحصاءات المرنة:

• المتوسط
• النطاق الربعي

فيما يلي أمثلة على الإحصائيات التي لا تصمد :

• المتوسط
• الانحراف المعياري
• مرتب

يوضح المثال التالي الفرق بين الإحصائيات المرنة وغير المقاومة.

مثال: إحصائيات المقاومة وغير المقاومة

لنفترض أن لدينا مجموعة البيانات التالية:

مجموعة البيانات: 2، 5، 6، 7، 8، 13، 15، 18، 22، 24، 29

باستخدام الآلة الحاسبة أو البرامج الإحصائية، يمكننا حساب قيمة إحصائيات الاحتفاظ التالية لمجموعة البيانات هذه:

• المتوسط: 13
• المدى الربعي: 13.5

يمكننا أيضًا حساب قيمة الإحصائيات غير المرنة التالية لمجموعة البيانات هذه:

• المتوسط: 13.54
• الانحراف المعياري: 8.82
• النطاق: 27

فكر الآن فيما إذا كانت مجموعة البيانات هذه تحتوي على قيمة متطرفة مضافة:

مجموعة البيانات: 2، 5، 6، 7، 8، 13، 15، 18، 22، 24، 29، 450

يمكننا مرة أخرى حساب قيمة الإحصائيات المرنة التالية لمجموعة البيانات هذه:

• المتوسط: 14
• المدى الربعي: 15.75

يمكننا أيضًا حساب قيمة الإحصائيات غير المرنة التالية لمجموعة البيانات هذه:

• المتوسط: 49.92
• الانحراف المعياري: 126.27
• النطاق: 448

لاحظ مدى تغير إحصائيات عدم المقاومة بمجرد إضافة قيمة متطرفة إلى مجموعة البيانات:

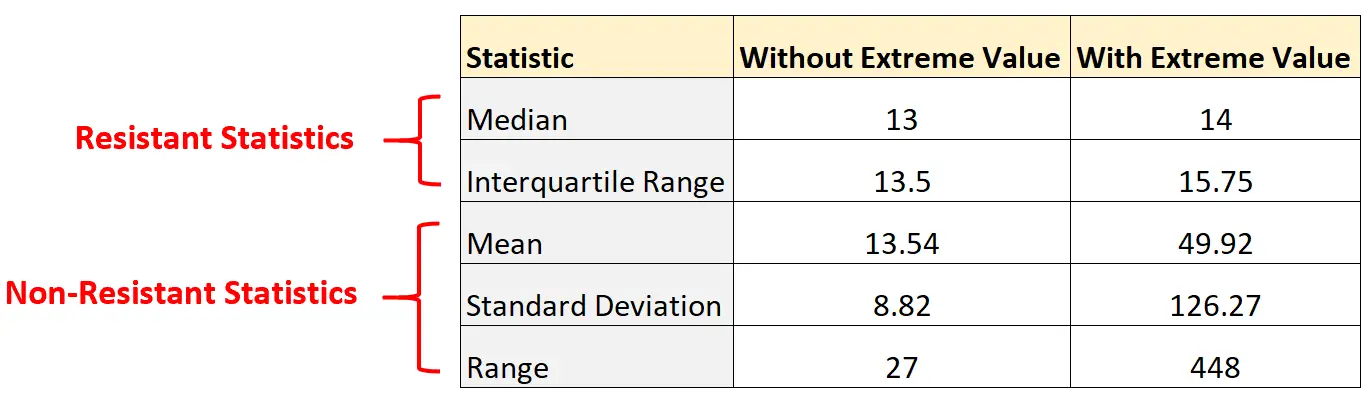
وعلى العكس من ذلك، فإن إحصائيات المقاومين لم تتغير كثيراً. لم يتغير النطاق المتوسط والربعي إلا قليلاً.

متى تستخدم الإحصائيات المرنة

الإحصائيات الأكثر استخدامًا لقياس مركز وتشتت القيم في مجموعة البيانات هي المتوسط والانحراف المعياري على التوالي.

لسوء الحظ، كل من هذه الإحصائيات حساسة للقيم المتطرفة. لذلك، إذا كانت القيم المتطرفة موجودة في مجموعة بيانات، فلن يصف المتوسط والانحراف المعياري بدقة توزيع القيم في مجموعة البيانات.

بدلاً من ذلك، يوصى باستخدام النطاق المتوسط والربيعي لقياس مركز وتشتت القيم في مجموعة البيانات في حالة وجود القيم المتطرفة، حيث أن كلا من هذه الإحصائيات قوية .

مصادر إضافية

كيف تؤثر القيم المتطرفة على المتوسط؟
متى يتم استخدام المتوسط مقابل الوسيط
متى يتم استخدام المدى الربيعي مقابل الانحراف المعياري