ما يعتبر "ضعيفاً"؛ علاقة؟
في الإحصاء، نسعى غالبًا إلى فهم كيفية ارتباط متغيرين ببعضهما البعض. على سبيل المثال، قد نريد أن نعرف:
- ما العلاقة بين عدد الساعات التي يدرسها الطالب والدرجة التي يحصل عليها في الامتحان؟
- ما العلاقة بين درجة الحرارة الخارجية وعدد قطع الآيس كريم التي تبيعها شاحنة الطعام؟
- ما هي العلاقة بين الدولارات التي يتم إنفاقها على الإعلانات وإجمالي الإيرادات المكتسبة لشركة معينة؟
في كل سيناريو، نريد أن نفهم العلاقة بين متغيرين.
إحدى الطرق الأكثر شيوعًا لقياس العلاقة بين متغيرين هي استخدام معامل ارتباط بيرسون ، وهو مقياس للارتباط الخطي بين متغيرين.
يأخذ دائمًا قيمة بين -1 و1 حيث:
- يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
- يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
- يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين
غالبًا ما يُشار إليه بـ r ، وهذا الرقم يساعدنا على فهم قوة العلاقة بين متغيرين. كلما اقتربت r من الصفر، ضعفت العلاقة بين المتغيرين .
ومن المهم ملاحظة أن متغيرين يمكن أن يكون لهما علاقة إيجابية ضعيفة أو علاقة سلبية ضعيفة.
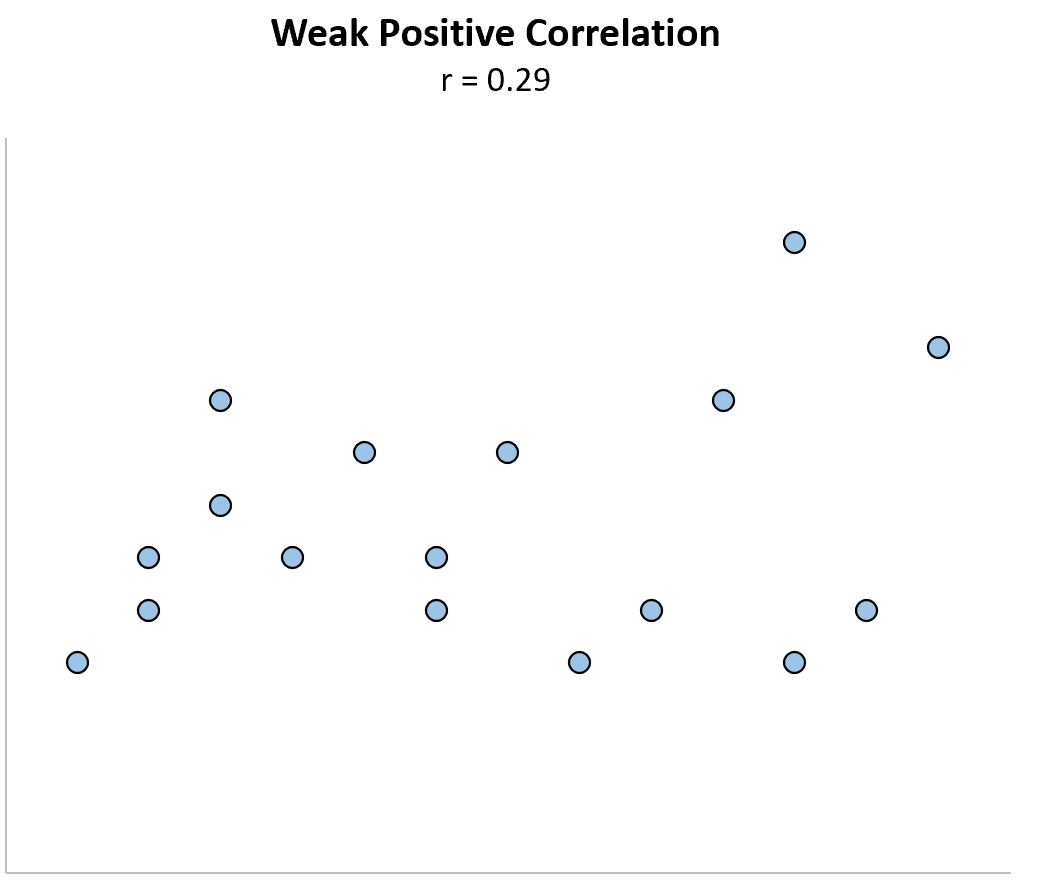
الارتباط الإيجابي الضعيف: عندما يزيد أحد المتغيرات، يميل المتغير الآخر إلى الزيادة أيضًا، ولكن بشكل ضعيف أو غير موثوق.
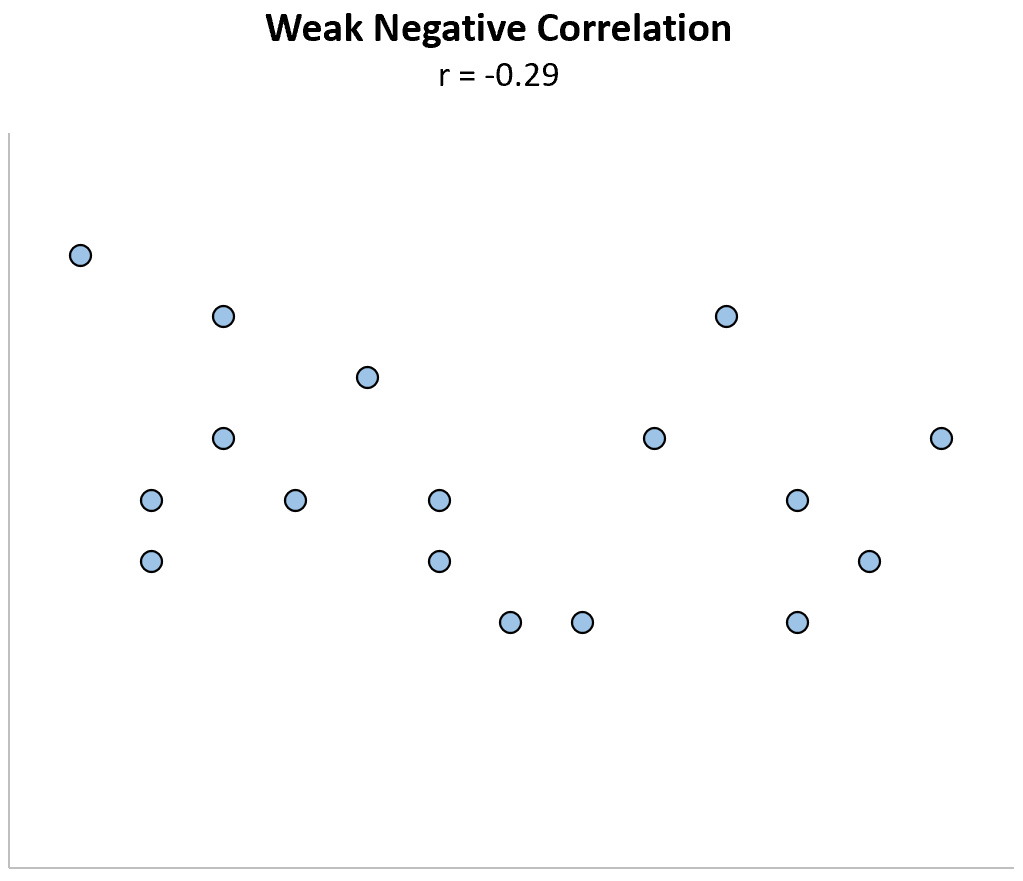
الارتباط السلبي المنخفض: عندما يزيد أحد المتغيرات، يميل المتغير الآخر إلى الانخفاض، ولكن فقط بشكل ضعيف أو غير موثوق.
يوضح الجدول التالي القاعدة الأساسية لتفسير قوة العلاقة بين متغيرين بناءً على قيمة r :
| القيمة المطلقة لل ص | قوة العلاقة |
|---|---|
| ص <0.25 | لا علاقة |
| 0.25 < ص <0.5 | علاقة ضعيفة |
| 0.5 < ص < 0.75 | علاقات معتدلة |
| ص > 0.75 | علاقة قوية |
يعتبر الارتباط بين متغيرين منخفضًا إذا كانت القيمة المطلقة لـ r تتراوح بين 0.25 و0.5.
ومع ذلك، فإن تعريف الارتباط “الضعيف” يمكن أن يختلف من مجال إلى آخر.
طبي
في المجالات الطبية، غالبًا ما يكون تعريف العلاقة “الضعيفة” أقل بكثير. إذا كانت العلاقة بين تناول دواء معين وتقليل النوبات القلبية هي r = 0.2، فيمكن اعتبار ذلك “لا علاقة” في مجالات أخرى، ولكن في الطب يعتبر الأمر مهمًا بدرجة كافية بحيث يستحق تناول الدواء لتقليل خطر الإصابة بالنوبات القلبية. . الإصابة بنوبة قلبية.
الموارد البشرية
في مجال مثل الموارد البشرية، يتم أيضًا استخدام الارتباطات الأقل في كثير من الأحيان. على سبيل المثال، تبين أن العلاقة بين المعدل التراكمي في الكلية والأداء الوظيفي تبلغ تقريبًا r = 0.16 . هذا رقم منخفض جدًا، لكنه مهم بدرجة كافية بحيث يجب على الشركة على الأقل أخذه بعين الاعتبار أثناء عملية المقابلة.
تكنولوجيا
في مجالات التكنولوجيا، قد يلزم أن يكون الارتباط بين المتغيرات أعلى بكثير ليتم اعتباره “منخفضًا”. على سبيل المثال، إذا قامت شركة ما بإنشاء سيارة ذاتية القيادة وكان الارتباط بين قرارات انعطاف السيارة واحتمال تجنب وقوع حادث هو r = 0.95 ، فيمكن اعتبار ذلك ارتباطًا “ضعيفًا” وربما يكون أضعف من أن تتمكن السيارة من ذلك تعتبر آمنة، لأن القرار الخاطئ يمكن أن يكون قاتلا.
استخدم مخططات التشتت لتصور الارتباطات
عند حساب معامل الارتباط بين متغيرين، من المفيد إنشاء مخطط تبعثر لتصور الارتباط أيضًا.
وعلى وجه الخصوص، تقدم السحب النقطية ميزتين:
1. يمكن أن تساعدك مخططات التشتت في تحديد القيم المتطرفة التي تؤثر على معامل الارتباط.
يمكن أن يكون للقيمة المتطرفة تأثير كبير على معامل الارتباط. خذ بعين الاعتبار المثال أدناه، حيث يكون للمتغيرين X و Y معامل ارتباط بيرسون r = 0.91 .
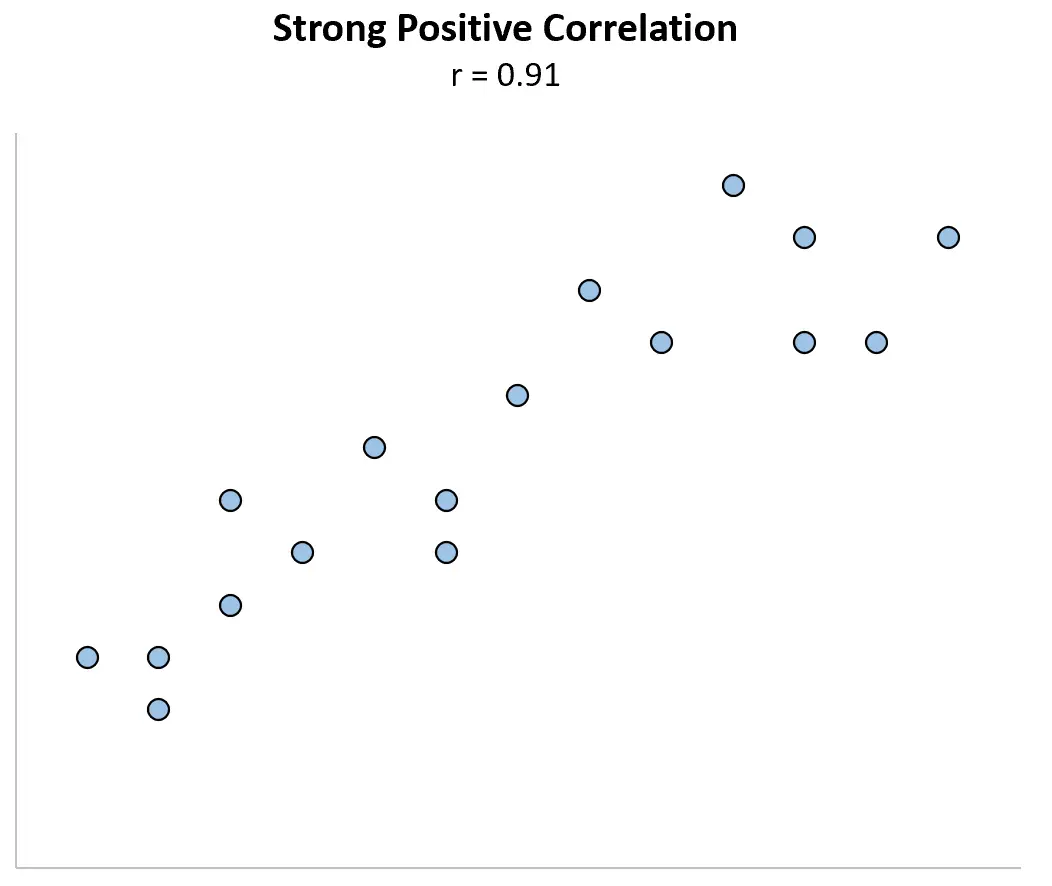
تخيل الآن أننا قمنا بتغيير نقطة البيانات الأولى لتصبح أكبر بكثير. يصبح معامل الارتباط فجأة r = 0.29 .
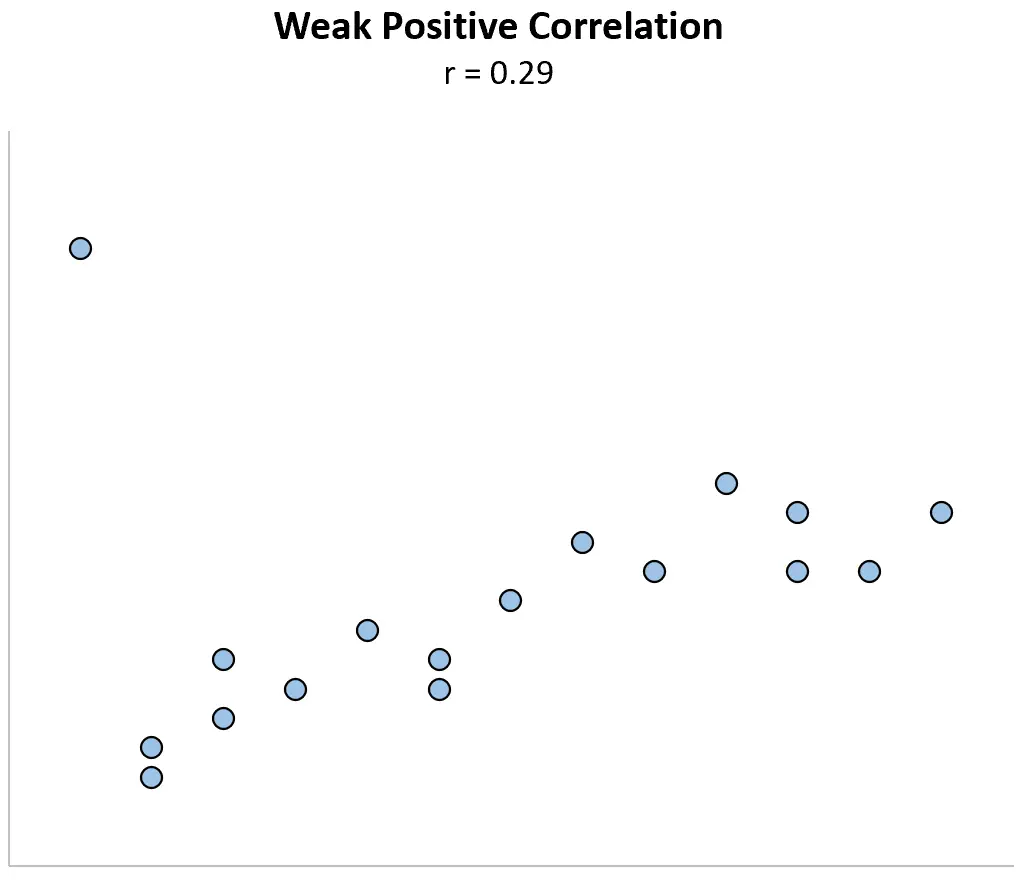
تعمل نقطة البيانات الفردية هذه على تغيير معامل الارتباط من علاقة إيجابية قوية إلى علاقة إيجابية ضعيفة.
(2) يمكن أن تساعدك مخططات التشتت في تحديد العلاقات غير الخطية بين المتغيرات.
يخبرنا معامل ارتباط بيرسون ببساطة ما إذا كان هناك متغيرين مرتبطين خطيًا . ولكن حتى لو أخبرنا معامل ارتباط بيرسون أن متغيرين غير مرتبطين، فمن الممكن أن يكون بينهما نوع من العلاقة غير الخطية.
على سبيل المثال، ضع في اعتبارك مخطط التشتت أدناه بين المتغيرين X و Y ، حيث يكون الارتباط بينهما r = 0.00 .
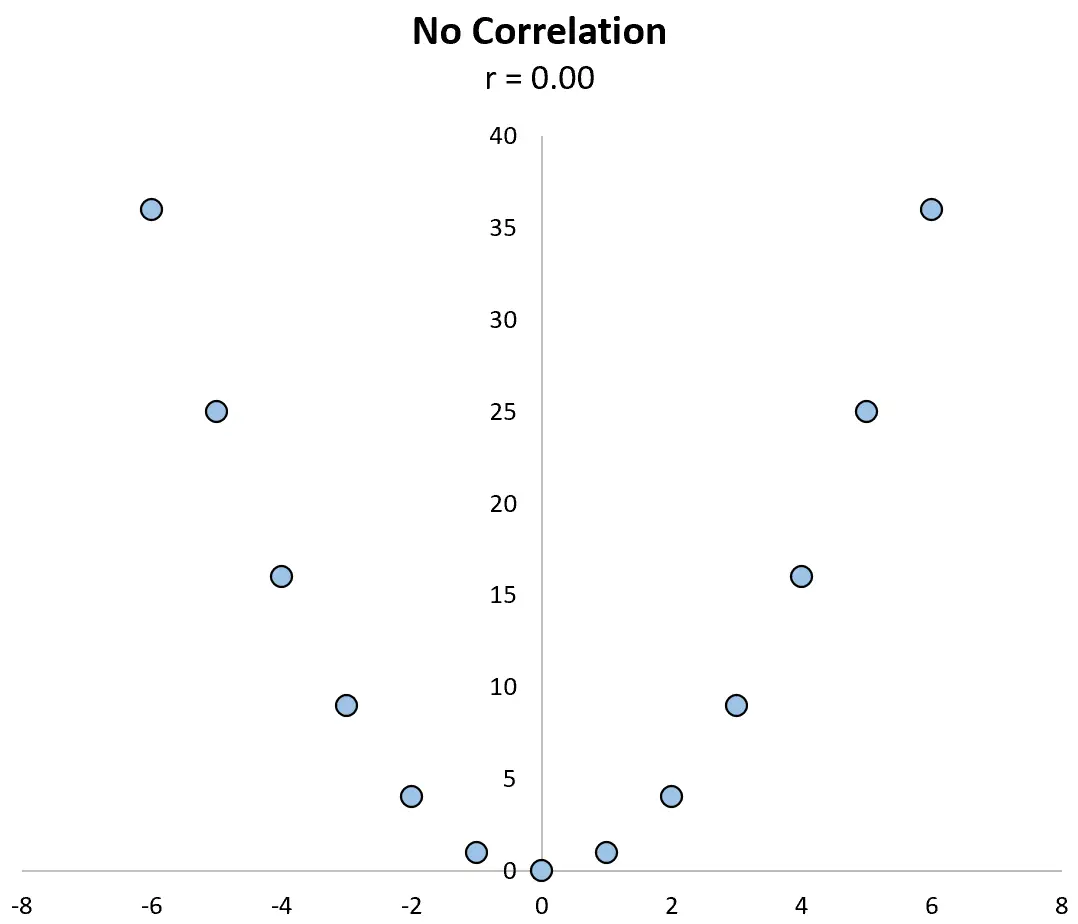
من الواضح أن المتغيرات ليس لها علاقة خطية، لكن لديها علاقة غير خطية: قيم y هي ببساطة قيم x مربعة.
لا يمكن لمعامل الارتباط وحده اكتشاف هذه العلاقة، لكن مخطط التشتت يمكنه ذلك.
خاتمة
في ملخص:
1. بشكل عام، يعتبر معامل الارتباط بين 0.25 و 0.5 ارتباطاً “ضعيفاً” بين متغيرين.
2. قد تختلف هذه القاعدة من منطقة إلى أخرى. على سبيل المثال، يمكن اعتبار الارتباط الأقل بكثير ضعيفًا في المجال الطبي مقارنة بالمجال التكنولوجي. تأكد من استخدام خبرتك في الموضوع لتحديد ما يعتبر ارتباطًا منخفضًا.
3. عند استخدام معامل الارتباط لوصف العلاقة بين متغيرين، من المفيد أيضًا إنشاء مخطط مبعثر حتى تتمكن من تحديد القيم المتطرفة في مجموعة البيانات بالإضافة إلى العلاقة غير الخطية المحتملة.
مصادر إضافية
ما الذي يعتبر ارتباطًا “قويًا”؟
حاسبة مصفوفة الارتباط
الارتباط مقابل. جمعية: ما هو الفرق؟