مبرهنة بايز

تشرح هذه المقالة ما هي نظرية بايز وفيما يتم استخدامها في الاحتمالات والإحصاء. وهكذا سوف تكتشف ما هي صيغة نظرية بايز، والأمثلة المحلولة لنظرية بايز، وما هي تطبيقات هذه النظرية.

ما هي نظرية بايز؟

في نظرية الاحتمالات، نظرية بايز هي قانون يستخدم لحساب احتمالية حدث ما عند معرفة معلومات مسبقة عن هذا الحدث.

وبشكل أكثر تحديدًا، تربط نظرية بايز رياضيًا بين احتمال وقوع الحدث A بمعلومية الحدث B إلى احتمال B بمعلومية A.

على سبيل المثال، إذا كنت تعرف مسبقًا احتمالية إصابة شخص ما بالصداع عند إصابته بالأنفلونزا، فيمكنك استخدام نظرية بايز لتحديد احتمالية إصابة الشخص بالأنفلونزا عند إصابته بالصداع.

نظرية بايز لها العديد من التطبيقات، على سبيل المثال، يتم استخدامها في الطب أو الاقتصاد أو التكنولوجيا لحساب احتمالات أحداث معينة مشروطة بأحداث أخرى. أدناه، سوف نتناول بالتفصيل التطبيقات المختلفة لنظرية بايز.

تم اختراع نظرية بايز من قبل عالم الرياضيات الإنجليزي توماس بايز (1702-1761)، على الرغم من نشرها بعد وفاته في عام 1763.

صيغة نظرية بايز

تقول نظرية بايز أنه بالنظر إلى عينة من الفضاء مكونة من مجموعة من الأحداث المتنافية {A ₁ , A ₂ ,…, A _i ,…, A _n } والتي لا تكون احتمالاتها صفرًا وحدث آخر B ، يمكننا ربط الشرطية رياضيًا احتمال A _i بالنظر إلى الحدث B مع الاحتمال المشروط لـ B بالنظر إلى A _i .

لذا، فإن صيغة نظرية بايز ، المعروفة أيضًا باسم قاعدة بايز ، هي:

ذهب:

• 

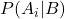
  هو الاحتمال الشرطي للحدث A _في ضوء الحدث B، ويسمى الاحتمال الخلفي.

• 

  هو الاحتمال الشرطي للحدث B نظرا للحدث A _i .

• 

  هو احتمال وقوع الحدث A _i ، ويسمى بالاحتمال القبلي.

لاحظ أن مقام صيغة نظرية بايز هو الاحتمال الإجمالي للحدث B.

مثال على نظرية بايز

بمجرد أن نرى تعريف نظرية بايز وما هي صيغتها، سنرى مثالًا محلولاً لكيفية حساب الاحتمال باستخدام نظرية بايز لفهم المفهوم بشكل أفضل.

• يبيع متجر إلكترونيات ثلاث علامات تجارية من أجهزة التلفزيون: X وY وZ. وتشير التقديرات إلى أن 20% من المبيعات عبارة عن أجهزة تلفزيون ذات علامة تجارية معيبة، و3% من أجهزة تلفزيون ذات علامة تجارية Y معيبة، و4% من أجهزة تلفزيون ذات علامة تجارية Z معيبة. نظرًا لوجود تلفزيون معيب، ما هو احتمال أن يكون تلفزيونًا من العلامة التجارية Z؟

يعطينا التمرين احتمالات قيام العميل بشراء كل علامة تجارية من أجهزة التلفزيون:

• الحدث أ ₁ : يشتري العميل تلفزيونًا من العلامة التجارية X → P(A ₁ )=0.20
• الحدث أ ₂ : يشتري العميل تلفزيونًا ماركة Y → P(A ₂ )=0.50
• الحدث أ ₃ : يشتري العميل تلفزيون Z من العلامة التجارية → P(A ₃ )=0.30

بالإضافة إلى ذلك، تعطينا القراءة أيضًا احتمالية وجود عيب في جهاز تلفزيون من كل علامة تجارية:

الحدث ب: التلفزيون معيب

• B|A ₁ : نظرًا لعلامة تجارية X للتلفزيون، فإن التليفزيون معيب → P(B|A ₁ )=0.05
• B|A ₂ : نظرًا لعلامة تجارية Y للتلفزيون، فإن التليفزيون معيب → P(B|A ₂ )=0.03
• B|A ₃ : بالنظر إلى تلفزيون من العلامة التجارية Z، يكون التلفزيون معيبًا → P(B|A ₃ )=0.04

لذا فإن شجرة الاحتمالات لجميع الأحداث التي تهمنا هي كما يلي:

لذا، لحساب احتمال أن تكون العلامة التجارية Z، في حالة وجود تلفزيون معيب، يجب أن نستخدم الصيغة من نظرية بايز:

باستخدام المصطلحات المستخدمة في هذا المثال، تبدو صيغة بايز كما يلي:

وبالتالي، فإن حساب احتمال أن يكون تلفزيون معيب معين هو العلامة التجارية Z هو كما يلي:

في الختام، فإن احتمال أن يكون التلفزيون معيبًا، فهو علامة تجارية Z هو 32%.

تطبيقات نظرية بايز

هناك العديد من التطبيقات لنظرية بايز، بما في ذلك:

1. الاختبارات الطبية : تُستخدم نظرية بايز بشكل متكرر في الطب لتحديد احتمال اجتياز الاختبارات التشخيصية. على سبيل المثال، في حالة اختبار فيروس نقص المناعة البشرية، يمكن استخدام النظرية لحساب احتمال إصابة الشخص بالفيروس بالفعل إذا كانت نتيجة الاختبار إيجابية.
2. التحليل المالي : في مجال التمويل، يتم استخدام نظرية بايز لحساب احتمال حدوث أحداث اقتصادية معينة، مثل الزيادة أو النقصان في قيمة الأسهم، في ضوء مجموعة من المتغيرات الاقتصادية.
3. أبحاث السوق : تتيح نظرية بايز إمكانية تحديد، على سبيل المثال، احتمالية قيام الشخص بشراء منتج ما بعد رؤية إعلان لهذا المنتج.
4. التنبؤ بالطقس : تستخدم نماذج الطقس أيضًا نظرية بايز لتحديد احتمالية تحقق تنبؤات جوية معينة بناءً على البيانات المرصودة. وهذا يحسن دقة التنبؤات المناخية.
5. أمن الكمبيوتر – في الأمن السيبراني، يمكن تطبيق نظرية بايز لتحديد احتمالية أن يكون النشاط المشبوه هجومًا حقيقيًا على نظام الكمبيوتر.

حل مشاكل نظرية بايز

التمرين 1

وتشير التقديرات إلى أن 1% من السكان يعانون من بعض الأمراض. وتبلغ دقة اختبار الكشف عن هذا المرض 95% للحالات الإيجابية و90% للحالات السلبية. إذا كانت نتيجة اختبار شخص تم اختياره عشوائيًا إيجابية، فما هو احتمال إصابته بالمرض بالفعل؟

بيان التمرين يعطينا الاحتمالات التالية:

ج ₁ : الشخص مصاب بالمرض → P( _A1 )=0.01
ج ₂ : الشخص غير مصاب بالمرض → P( _A2 )=0.99

ب: الاختبار إيجابي
B|A ₁ : يكون الاختبار إيجابيًا عندما يكون الشخص مصابًا بالمرض → P(B|A ₁ )=0.95
B|A ₂ : يكون الاختبار إيجابيًا عندما لا يكون الشخص مصابًا بالمرض → P(B|A ₂ )=1-0.90=0.10

ثم، لحساب احتمال أن يكون الشخص الذي تم اختياره عشوائيًا مصابًا بالمرض بالفعل عندما تكون نتيجة اختباره إيجابية، يجب تطبيق قاعدة بايز:

لذلك نقوم باستبدال القيم في الصيغة وإجراء حساب الاحتمال:

باختصار، فإن احتمال أن تكون نتيجة اختبار الشخص الذي تم اختياره عشوائيًا إيجابية وأن يكون مصابًا بالمرض بالفعل هي 8.76%.

تمرين 2

تشير التقديرات إلى أن احتمال ارتفاع السهم في يوم واحد هو 40%، واحتمال بقائه مستقرًا هو 10%، واحتمال انخفاضه هو 50%. علاوة على ذلك، نحن نعلم أنه عندما يرتفع السوق، هناك احتمال بنسبة 90% أن المحلل المالي سوف يتنبأ به بشكل صحيح، وأنه عندما يظل السوق مستقراً، فإن احتمال أن يكون التنبؤ صحيحاً هو 75%، وأنه في حالة الانخفاض، احتمالية التنبؤ الصحيح هي 75%. 85%.%. إذا توقع أحد المحللين أن السوق سوف ينخفض، فما مدى احتمالية سقوطه بالفعل؟

في هذه الحالة، يوفر لنا بيان التمرين الاحتمالات التالية:

ج ₁ : يرتفع السوق في يوم واحد ← P(A ₁ )=0.40
ج ₂ : يظل السوق مستقرًا على مدى يوم واحد ← P( _A2 )=0.10
ج ₃ : يرتفع السوق في يوم واحد ← P( _A3 )=0.50

ب: يتوقع المحلل أن السوق سوف ينخفض
B|A ₁ : توقع المحلل بشكل صحيح أن السوق سوف يرتفع ← P(B|A ₁ )=0.90
B|A ₂ : توقع المحلل بشكل صحيح أن السوق لا يزال مستقرًا → P(B|A ₂ )=0.75
B|A ₃ : توقع المحلل بشكل صحيح أن السوق سوف ينخفض ← P(B|A ₃ )=0.85

لتحديد احتمال قيام المحلل بالتنبؤ بأن السوق سوف ينخفض وأن هذا التنبؤ صحيح، نحتاج إلى استخدام صيغة نظرية بايز:

نستبدل قيم الاحتمال في صيغة بايز ونحسب الاحتمال:

ولذلك فإن احتمالية أن يكون المحلل على حق عندما يقول أن سوق الأسهم سوف ينخفض هو 49.42%.