كيفية العثور على متوسط الانحرافات المعيارية المتعددة
في بعض الأحيان قد ترغب في العثور على متوسط اثنين أو أكثر من الانحرافات المعيارية.
للقيام بذلك، يمكنك استخدام إحدى الصيغتين التاليتين، اعتمادًا على بياناتك:
الطريقة الأولى: تساوي حجم العينة
إذا كنت تريد العثور على متوسط الانحراف المعياري بين مجموعات k وكل مجموعة لها نفس حجم العينة، فيمكنك استخدام الصيغة التالية:
متوسط SD = √ ( ق 2 1 + ق 2 2 + … + ق ك 2 ) / ك
ذهب:
- sk : الانحراف المعياري للمجموعة k
- ك : العدد الإجمالي للمجموعات
الطريقة الثانية: أحجام العينات غير المتكافئة
إذا كنت تريد العثور على متوسط الانحراف المعياري بين مجموعات k وليس لكل مجموعة نفس حجم العينة، فيمكنك استخدام الصيغة التالية:
متوسط SD = √ ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 + … + (n k -1)s k 2 ) / (n 1 +n 2 + … + n k – ي)
ذهب:
- n k : حجم العينة للمجموعة k
- sk : الانحراف المعياري للمجموعة k
- ك : العدد الإجمالي للمجموعات
توضح الأمثلة التالية كيفية استخدام كل صيغة عمليًا.
الطريقة الأولى: حساب متوسط الانحرافات المعيارية لأحجام العينات المتساوية
لنفترض أننا نريد حساب متوسط الانحراف المعياري للمبيعات خلال فترات المبيعات الست التالية:
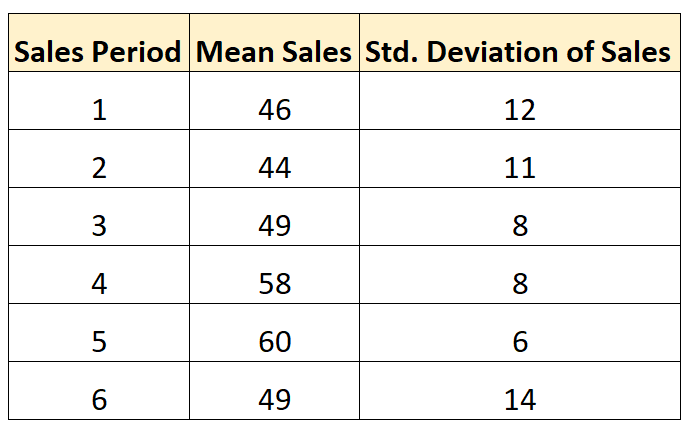
لنفترض أننا قمنا بنفس عدد معاملات البيع خلال كل فترة مبيعات. يمكننا استخدام الصيغة التالية لحساب متوسط الانحراف المعياري للمبيعات لكل فترة:
- متوسط الانحراف المعياري = √ ( ق 2 1 + ق 2 2 + … + ق ك 2 ) / ك
- متوسط الانحراف المعياري = √ (2 12 + 11 2 + 8 2 + 8 2 + 6 2 + 14 2 ) / 6
- متوسط الانحراف المعياري = 10.21
متوسط الانحراف المعياري للمبيعات لكل فترة هو 10.21 .
الطريقة الثانية: حساب متوسط الانحرافات المعيارية لأحجام العينات غير المتكافئة
لنفترض أننا نريد حساب متوسط الانحراف المعياري للمبيعات خلال فترات المبيعات الست التالية:
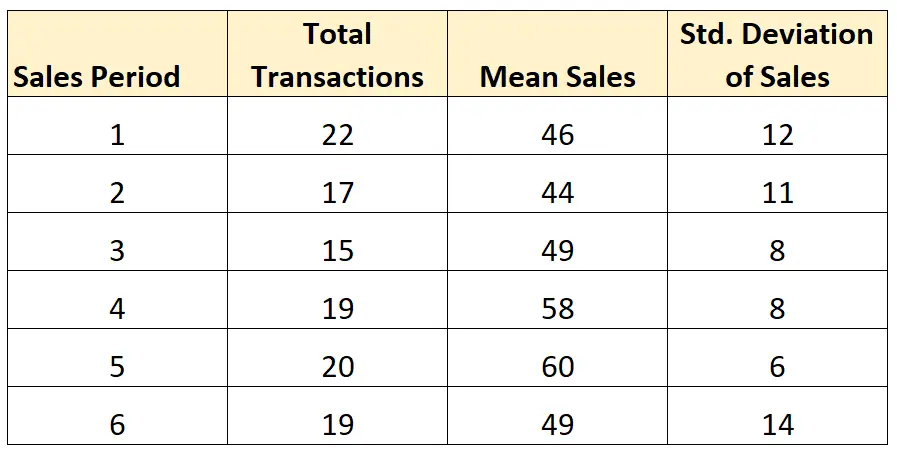
وبما أن حجم العينة (إجمالي المعاملات) ليس متساويا في كل فترة مبيعات، فسوف نستخدم الصيغة التالية لحساب متوسط الانحراف المعياري للمبيعات لكل فترة:
- متوسط SD = √ ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 + … + (n k -1)s k 2 ) / (n 1 +n 2 + … + n k – ي)
- متوسط SD = √ ((21)12 2 + (16)11 2 + (14)8 2 + (18)8 2 + (19)6 2 + (18)14 2 ) / 106
- يعني SD = 10.29
متوسط الانحراف المعياري للمبيعات لكل فترة هو 10.29 .
لاحظ أن متوسط الانحراف المعياري في المثالين كان متشابهًا تمامًا. وذلك لأن أحجام العينات (إجمالي المعاملات) في المثال الثاني كانت جميعها قريبة جدًا من بعضها البعض.
تختلف طريقتان لحساب متوسط الانحراف المعياري بشكل كبير فقط عندما تختلف أحجام العينات بشكل كبير بين المجموعات.
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر