متوسط الوزن

By دكتور بنيامين أندرسون زومار 6, 2023 إحصائيات 0 Comments

ونوضح هنا ما هو المتوسط المرجح وكيفية حسابه. ستتمكن من رؤية تمرين تم حله حول كيفية إيجاد المتوسط المرجح. والأكثر من ذلك، أنه يمكنك حساب المتوسط المرجح لأي مجموعة بيانات باستخدام الآلة الحاسبة في النهاية.

ما هو المتوسط المرجح؟

المتوسط المرجح هو مقياس لمركزية الإحصاء الوصفي. لحساب المتوسط المرجح، عليك أولاً ضرب كل بيانات إحصائية بوزنها (أو وزنها)، ثم إضافة جميع المنتجات، وأخيرًا قسمة المجموع المرجح على مجموع كل الأوزان.

وبعبارة أخرى، فإن صيغة المتوسط المرجح هي كما يلي:

حيث تمثل x _i كل عينة بيانات وw _i وزنها المقابل.

وبالتالي، كلما زاد وزن قطعة من البيانات، زادت أهميتها في حساب المتوسط المرجح. وبعبارة أخرى، كلما زاد وزن جزء من البيانات، كلما زاد تأثيره على نتيجة المتوسط المرجح.

يعد المتوسط المرجح مفيدًا بشكل خاص لحساب الدرجات، لأنه يسمح لك بتقييم التمارين أو الاختبارات التي تم إجراؤها خلال الدورة التدريبية بأهمية مختلفة. ويستخدم المتوسط المرجح أيضًا لحساب مؤشر أسعار المستهلك (مؤشر أسعار المستهلك)، وهو مؤشر لقياس أسعار السكان.

إلى جانب المتوسط المرجح، هناك أيضًا أنواع أخرى من المتوسطات مثل المتوسط الهندسي، والمتوسط الحسابي، والمتوسط المربع، والمتوسط التوافقي.

كيفية حساب المتوسط المرجح

لحساب المتوسط المرجح يجب اتباع الخطوات التالية:

اضرب كل البيانات الإحصائية بوزنها المقابل.
أضف جميع المنتجات المحسوبة في الخطوة السابقة.
اقسم المبلغ المرجح أعلاه على مجموع كل الأوزان.
والنتيجة التي تم الحصول عليها هي المتوسط المرجح للعينة الإحصائية.

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب المتوسط المرجح لأي مجموعة بيانات.

مثال المتوسط المرجح

بالنظر إلى تعريف المتوسط المرجح، سنحل الآن تمرينًا لفهم كيفية الحصول على المتوسط المرجح من مجموعة من البيانات بشكل كامل.

حصل طالب في الصف الأول الثانوي في مادة الرياضيات على الدرجات التالية: 7 في الامتحان الجزئي الذي يمثل 30%، 9 في العمل الجماعي الذي يساوي 20%، 6 في التمارين المعطاة في الفصل مع الترجيح 10% و8 في الامتحان النهائي الذي يكون وزنه 40%. ما هي درجتك النهائية في المادة؟

لتحديد علامة الطالب يجب إيجاد المتوسط المرجح بالقيم التي تعطيها العبارة. للقيام بذلك، نطبق صيغة المتوسط المرجح:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

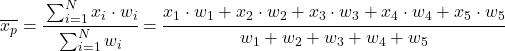
درجة كل تسليم هي القيمة الإحصائية ونسبتها تتوافق مع وزن القيمة المذكورة. لذلك، نستبدل القيم والأوزان في الصيغة ونجري حساب المتوسط المرجح:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

وبالتالي فإن الدرجة النهائية في الرياضيات لهذا الطالب ستكون 7.7 لأن هذه هي النتيجة التي تم الحصول عليها من المتوسط المرجح.

حاسبة المتوسط المرجح

أدخل البيانات من أي عينة إحصائية وأوزانها في الآلة الحاسبة أدناه لحساب المتوسط المرجح لها.

أدخل البيانات الإحصائية في المربع الأول وأوزانها في المربع الثاني. يجب عليك كتابة الأوزان بنفس ترتيب البيانات وبالتنسيق العشري. يجب أن يتم فصل جميع الأرقام بمسافة وإدخالها باستخدام النقطة كفاصل عشري.

الأوزان الموحدة

كما رأينا، في المتوسط المرجح، الوزن هو القيمة التي تعطى لكل جزء من البيانات لإعطائها أهمية أكبر أو أقل. لذلك، إذا كانت المعلومات مهمة جدًا، فسيكون لها وزن كبير جدًا، ولكن إذا لم تكن المعلومات ذات صلة كبيرة، فسيكون لها وزن منخفض جدًا.

حسنًا، الوزن الطبيعي هو أحد أنواع الترجيح المستخدم للحصول على المتوسط المرجح دون الحاجة إلى إجراء أي قسمة.

الوزن الطبيعي هو وزن عنصر البيانات مقسومًا على مجموع كل الأوزان.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

وبالتالي فإن مجموع جميع الأوزان الطبيعية يساوي واحدًا:

$\sum_{i=1}^N w_i'=1$

لذلك، لحساب المتوسط المرجح بالأوزان الطبيعية ، ما عليك سوى ضرب كل عنصر بيانات بوزنه الطبيعي:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

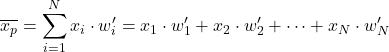
على سبيل المثال، لدينا عينة إحصائية بياناتها هي 24، 35، 17، 41 وأوزان كل منها هي 4، 9، 6، 3. للعثور على المتوسط المرجح لمجموعة البيانات هذه، يمكننا أولاً حساب الأوزان المعيارية عن طريق قسمة كل وزن بمجموع كل الأوزان:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

والآن فقط قم بضرب كل البيانات بوزنها الطبيعي وستكون النتيجة المتوسط المرجح:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

الفرق بين المتوسط المرجح والمتوسط الحسابي

ويتم حساب المتوسط المرجح والمتوسط الحسابي بنفس الطريقة، حيث يجب إجراء عمليات مماثلة. في المتوسط المرجح، يتم ضرب كل نقطة بيانات في وزنها وتقسيمها على مجموع الأوزان، ولكن في المتوسط الحسابي، يتم جمع جميع البيانات معًا وتقسيمها على إجمالي عدد نقاط البيانات.

الفرق بين المتوسط المرجح والمتوسط الحسابي يكمن في مفهومه، ففي المتوسط الحسابي يعتبر أن جميع البيانات لها نفس القيمة، أما في المتوسط المرجح لكل بيانات وزن مختلف.

لاحظ أنه إذا كانت جميع الأوزان متساوية، فإن المتوسط المرجح يعادل المتوسط الحسابي. يمكنك رؤية الدليل الرياضي أدناه:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر