معدل الجذر التربيعي

By دكتور بنيامين أندرسون زومار 6, 2023 إحصائيات 0 Comments

نوضح هنا ما هو جذر متوسط المربعات وكيفية حسابه. بالإضافة إلى ذلك، سوف تتعلم مزايا وعيوب استخدام المتوسط والتمرين الذي تم حله خطوة بخطوة. وأخيرًا، ستتمكن من حساب الجذر التربيعي لأي مجموعة بيانات باستخدام الآلة الحاسبة في نهاية المقالة.

ما هو المربع المتوسط؟

جذر متوسط المربع هو مقياس لمركزية الإحصاء الوصفي. جذر متوسط المربع يساوي الجذر التربيعي للوسط الحسابي لمربعات البيانات.

يُطلق على جذر متوسط التربيع أيضًا اسم جذر متوسط التربيع ، أو RMS .

وبالتالي فإن صيغة الوسط التربيعي هي كما يلي:

يكون المتوسط المربع مفيدًا بشكل خاص عندما يأخذ المتغير الإحصائي قيمًا موجبة وسالبة، لأنه من خلال تربيع كل جزء من البيانات، تصبح جميع القيم موجبة. لذلك، يتم استخدام المربع المتوسط لتحليل المتغيرات التي لا تكون فيها الإشارة مهمة، بل قيمتها المطلقة.

على سبيل المثال، يتم استخدام مربع الوسط لدراسة أخطاء القياس، لأننا في هذه الحالات لا ننظر إلى ما إذا كان الخطأ إيجابيا أم سلبيا، بل نقوم بتحليل حجم الخطأ عند القياس.

بالإضافة إلى ذلك، فإن مربعات الأعداد الكبيرة لها قيم أعلى بكثير من مربعات الأعداد الصغيرة، لذلك في المربع الأوسط تكون الأعداد الكبيرة أكثر أهمية من الأعداد الصغيرة.

المتوسط المربع هو نوع من المتوسط الإحصائي إلى جانب المتوسط الحسابي والمتوسط المرجح والمتوسط الهندسي والمتوسط التوافقي.

مزايا وعيوب جذر متوسط مربع

المتوسط التربيعي له مزايا وعيوب مقارنة بأنواع المتوسطات الأخرى.

الميزة الرئيسية للوسط التربيعي هي أنه يسمح لك بالحصول على تقدير تقريبي جيد جدًا لمتوسط قيمة المتغير المنفصل. من ناحية أخرى، فإن العيب الكبير للمتوسط المربع هو أن حسابه معقد للغاية، حيث يجب تنفيذ العديد من العمليات.

في المقابل، جذر متوسط التربيع مفيد جدًا لتحليل قياسات الخطأ. كما أنها تعطي أهمية أكبر بكثير للقيم العالية، على الرغم من أن هذه الخاصية تعني أن القياس الخاطئ سيغير نتيجة جذر متوسط التربيع بشكل كبير.

كيفية حساب جذر متوسط التربيع

لحساب جذر متوسط المربع يجب تنفيذ الخطوات التالية:

احسب مربع كل بيانات إحصائية.
أضف كل المربعات المحسوبة في الخطوة السابقة.
اقسم النتيجة على عدد عناصر البيانات في العينة.
أوجد الجذر التربيعي للقيمة السابقة.
والنتيجة التي تم الحصول عليها هي المتوسط المربع للعينة الإحصائية.

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب الجذر التربيعي لأي مجموعة بيانات.

يعني مثال مربع

بمجرد أن نعرف كيفية الحصول على جذر متوسط التربيع، سنحدد جذر متوسط مربع مجموعة من البيانات كمثال.

في أحد فصول مختبر الجامعة، يطلب الأستاذ من طلابه إجراء تجربة باستخدام المواد الكيميائية. الهدف من التجربة الكيميائية هو الحصول على محلول إجمالي قدره 3 لترات. حصلت المجموعات الطلابية على البيانات التالية:

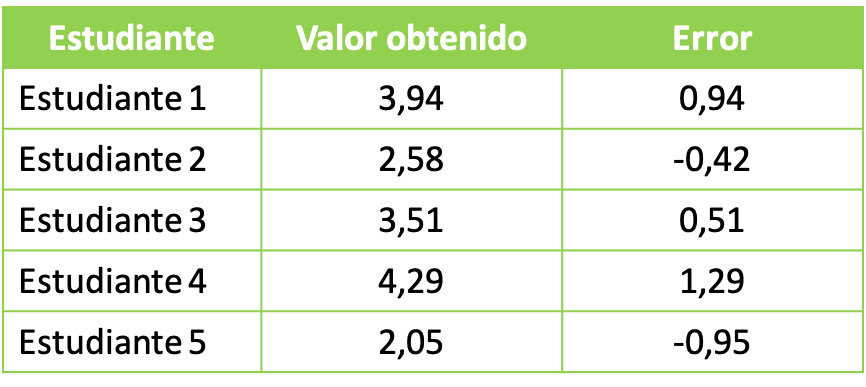
ومن أجل دراسة البيانات الإحصائية التي تم الحصول عليها، قمنا بحساب قيمة الوسط المربع مع الخطأ الذي حصلت عليه كل مجموعة. لذلك نطبق صيغة الوسط التربيعي:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

ونستبدل البيانات في الصيغة ونحسب جذر متوسط التربيع:

$\displaystyle RMS=\sqrt{\frac{0,94^2+(-0,42)^2+0,51^2+1,29^2+(-0,95)^2}{5}}=0,88$

وبالتالي، فإن متوسط الخطأ الذي تم الحصول عليه في التجربة، وفقًا لجذر متوسط التربيع، هو 0.88 لتر.

متوسط مربع حاسبة

أدخل البيانات من أي عينة إحصائية في الآلة الحاسبة التالية لحساب جذر متوسط مربعها. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر