مشكلة مونتي هول: شرح مرئي بسيط

في عرض ألعاب قديم يسمى Let’s Make a Deal ، قدم المضيف مونتي هول للمتسابقين ثلاثة أبواب.

يحتوي أحد الأبواب على جائزة بينما لا يحتوي البابان الآخران على جائزة.

سيطلب مونتي من المتسابق اختيار الباب الذي يعتقد أنه يحتوي على الجائزة.

بمجرد أن يختار المتسابق الباب، يقوم مونتي بعد ذلك بفتح الباب الذي لا يحتوي على الجائزة.

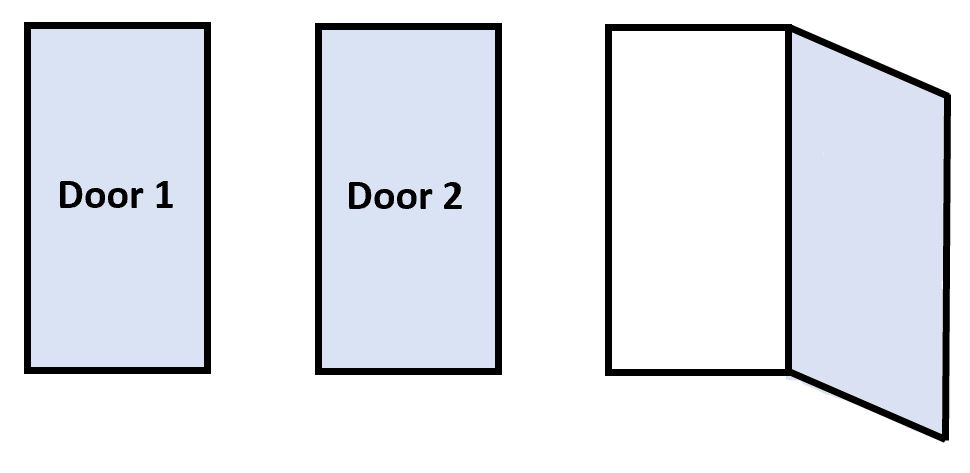
وبقيت الجائزة في أحد البابين المغلقين.

ثم يسأل مونتي المرشح عما إذا كان يريد تغيير الأبواب.

على الرغم من أنه قد يبدو من الصعب تصديق ذلك، فقد تبين أن تغيير الأبواب في هذه المرحلة من اللعبة يمنحك في الواقع فرصة أكبر للفوز.

تابع القراءة لتعرف السبب!

مشكلة مونتي هول موضحة بصريًا

لتوضيح لماذا يمنحك تغيير الأبواب احتمالية أكبر للفوز، فكر في السيناريوهات التالية التي تختار فيها الباب رقم 1 أولاً.

السيناريو 1: اخترت الباب 1 والجائزة موجودة بالفعل خلف الباب 1.

في هذه الحالة، مونتي سيفتح الباب 2 أو 3 ويظهر لك أنه لا يوجد شيء خلف أي من البابين. إذا بقيت مع الباب رقم 1، فستفوز .

السيناريو 2: اخترت الباب 1 والجائزة موجودة بالفعل خلف الباب 2.

في هذه الحالة، يجب على مونتي أن يفتح الباب رقم 3 ويظهر لك أنه لا يوجد شيء خلفه. إذا بقيت مع الباب رقم 1، فستخسر .

السيناريو 3: اخترت الباب 1 والجائزة موجودة بالفعل خلف الباب 3.

في هذه الحالة، يجب على مونتي أن يفتح الباب رقم 2 ويظهر لك أنه لا يوجد شيء خلفه. إذا بقيت مع الباب رقم 1، فستخسر .

هذه كلها نتائج محتملة إذا اخترت الباب رقم 1. لاحظ أنه إذا بقيت مع الباب رقم 1، فإنك توفر ثلث الوقت فقط. ولكن إذا قمت بالتغيير، فإنك توفر ثلثي الوقت.

يلخص الجدول التالي جميع السيناريوهات المحتملة في عرض اللعبة هذا بالإضافة إلى النتائج المرتبطة بالصيانة والتغيير:

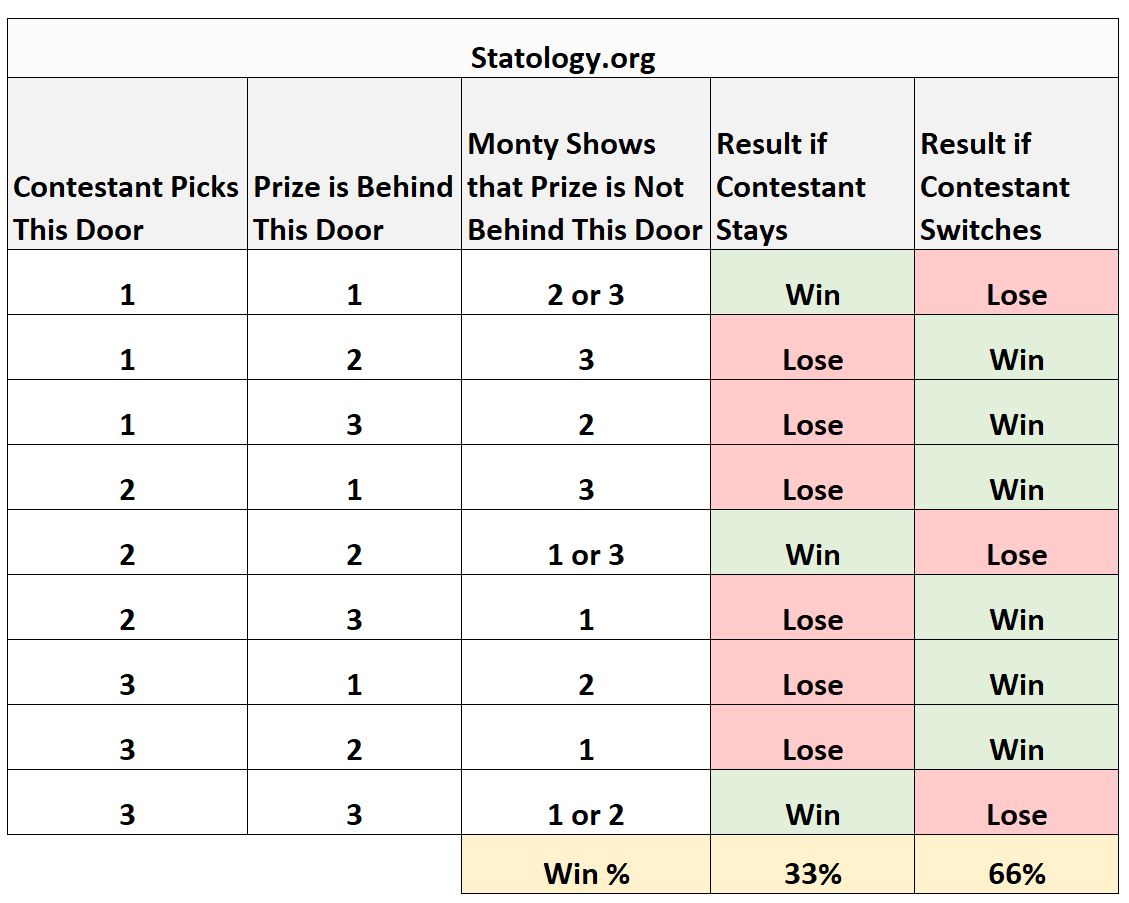
من الجدول، يمكننا أن نرى أنك تفوز بنسبة 33% من الوقت عندما تبقى، ولكنك تفوز بنسبة 66% من الوقت عندما تقوم بالتبديل.

لذا فإن تغيير الأبواب يزيد من احتمالية فوزك بالجائزة.

في حين أن هذا قد لا يبدو منطقيًا بشكل حدسي، إلا أن الرياضيات لا تكذب.