هل يمكن أن تكون نتيجة z سلبية؟

في الإحصائيات، تخبرنا النتيجة z عن عدد الانحرافات المعيارية للقيمة عن المتوسط . نستخدم الصيغة التالية لحساب درجة z:

ض = (X – μ) / σ

حيث X هي القيمة التي نقوم بتحليلها، μ هو المتوسط و σ هو الانحراف المعياري.

يمكن أن تكون النتيجة Z إيجابية أو سلبية أو صفر.

تشير درجة z الإيجابية إلى أن قيمة معينة أعلى من المتوسط، وتشير درجة z السالبة إلى أن قيمة معينة أقل من المتوسط، وتشير درجة الصفر من الألف إلى الياء إلى أن قيمة معينة تساوي المتوسط.

بعض الأمثلة يجب أن توضح ذلك.

أمثلة: حساب درجة Z

لنفترض أن لدينا مجموعة البيانات التالية التي توضح الارتفاع (بالبوصة) لمجموعة معينة من النباتات:

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

متوسط العينة لمجموعة البيانات هذه هو 13 والانحراف المعياري للعينة هو 5.51 .

1. ابحث عن النتيجة z للقيمة “8” في مجموعة البيانات هذه.

فيما يلي كيفية حساب درجة z:

ض = (X – μ) / σ = (8 – 13) / 5.51 = -0.91

وهذا يعني أن القيمة “8” هي 0.91 انحراف معياري أقل من المتوسط.

2. ابحث عن النتيجة z للقيمة “13” في مجموعة البيانات هذه.

فيما يلي كيفية حساب درجة z:

ض = (X – μ) / σ = (13 – 13) / 5.46 = 0

وهذا يعني أن القيمة “13” تساوي تمامًا المتوسط.

3. ابحث عن النتيجة z للقيمة “20” في مجموعة البيانات هذه.

فيما يلي كيفية حساب درجة z:

ض = (X – μ) / σ = (20 – 13) / 5.46 = 1.28

وهذا يعني أن القيمة “20” هي 1.28 انحراف معياري فوق المتوسط.

كيفية تفسير درجات Z

يخبرنا مخطط AZ عن النسبة المئوية للقيم التي تقل عن درجات Z معينة. بعض الأمثلة يجب أن توضح ذلك.

مثال 1: درجات Z السلبية

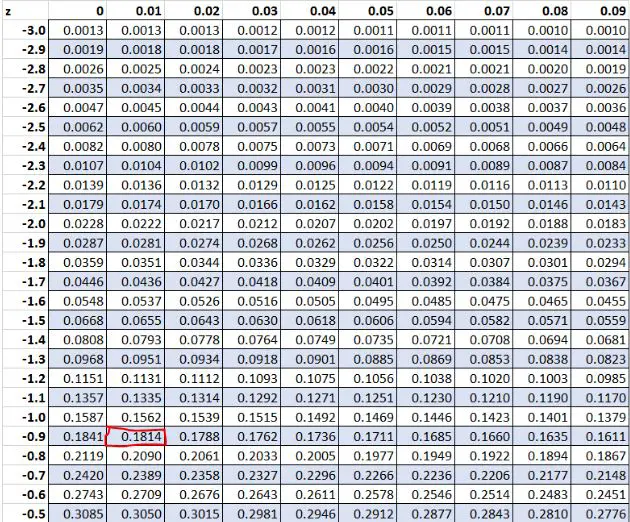
في وقت سابق، وجدنا أن القيمة الأولية “8” في مجموعة البيانات الخاصة بنا كانت لها درجة Z تبلغ -0.91 . وبحسب الجدول Z فإن 18.14% من القيم أقل من هذه القيمة.

مثال 2: درجات Z تساوي الصفر

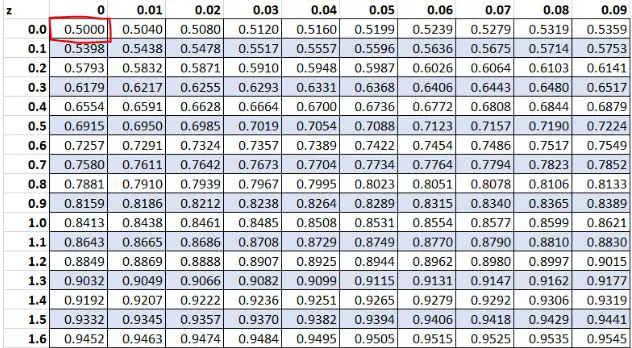
في وقت سابق، وجدنا أن القيمة الأولية “13” في مجموعة البيانات الخاصة بنا كانت لها درجة z تبلغ 0 . وبحسب الجدول Z فإن 50.00% من القيم أقل من هذه القيمة.

مثال 3: درجات Z الإيجابية

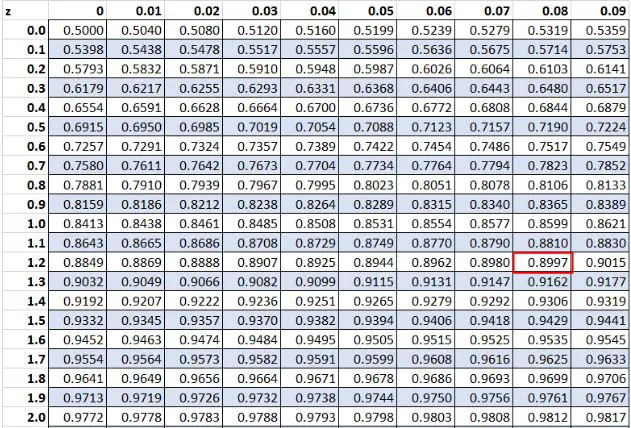
في وقت سابق، وجدنا أن القيمة الأولية “20” في مجموعة البيانات لدينا كانت لها درجة Z تبلغ 1.28 . وبحسب الجدول Z فإن 89.97% من القيم أقل من هذه القيمة.

خاتمة

يمكن أن تأخذ درجات Z أي قيمة بين اللانهاية السالبة واللانهاية الإيجابية، ولكن معظم درجات Z تقع ضمن انحرافين معياريين عن المتوسط. هناك في الواقع قاعدة في الإحصاء تُعرف باسم القاعدة العامة ، والتي تنص على أنه بالنسبة لمجموعة بيانات معينة ذات توزيع طبيعي:

• 68% من قيم البيانات تقع ضمن انحراف معياري واحد عن الوسط.
• 95% من قيم البيانات تقع ضمن انحرافين معياريين عن المتوسط.
• 99.7% من قيم البيانات تقع ضمن ثلاثة انحرافات معيارية عن المتوسط.

كلما ارتفعت القيمة المطلقة للدرجة z، كلما ابتعدت القيمة الأولية عن متوسط مجموعة البيانات. كلما انخفضت القيمة المطلقة للدرجة z، كلما كانت القيمة الأولية أقرب إلى متوسط مجموعة البيانات.

مواضيع ذات صلة:

قواعد حاسبة الإبهام
كيفية تطبيق القاعدة الأساسية في Excel