الوسائل الهندسية
نوضح في هذا المقال ما هو الوسط الهندسي وكيف يتم حسابه وما الفرق بين الوسط الهندسي والوسط الحسابي. ستتمكن أيضًا من رؤية تمرين تم حله خطوة بخطوة للمتوسط الهندسي وما هي خصائص هذا النوع من المتوسط. وأخيرًا، ستجد آلة حاسبة لحساب المتوسط الهندسي لأي مجموعة بيانات.
ما هو الوسط الهندسي؟
المتوسط الهندسي هو مقياس لمركزية الإحصاء الوصفي. الوسط الهندسي لمجموعة من البيانات الإحصائية يساوي الجذر النوني لحاصل ضرب جميع القيم.
يُستخدم المتوسط الهندسي في تمويل الأعمال لحساب معدلات العائد ومتوسطات النسبة المئوية والفائدة المركبة.
وبالتالي فإن صيغة الوسط الهندسي هي كما يلي:

لا يمكن حساب المتوسط الهندسي إلا عندما تكون جميع البيانات في العينة موجبة. لأنه إذا كانت القيمة سالبة، فسيكون للجذر حل سالب أو لا يوجد حل، من ناحية أخرى، إذا كانت البيانات صفرًا فإن ضرب البيانات سيعطي صفرًا، وبالتالي فإن الوسط الهندسي يساوي 0.
والوسط الهندسي ليس هو النوع الوحيد من المتوسطات الموجودة، فهناك أيضًا الوسط الحسابي، والوسط المرجح، والوسط المربع، والوسط التوافقي.
الفرق بين الوسط الهندسي والوسط الحسابي
والفرق الرئيسي بين الوسط الهندسي والوسط الحسابي هو أن الوسط الهندسي أقل حساسية للقيم المتطرفة من الوسط الحسابي. بالإضافة إلى ذلك، يمكن حساب المتوسط الحسابي بالقيم السالبة والصفر، بينما لا يمكن حساب المتوسط الهندسي إلا بالقيم الموجبة.
وبالمثل، سيكون المتوسط الهندسي عمومًا أقل من المتوسط الحسابي لنفس مجموعة البيانات.
وتجدر الإشارة أيضًا إلى أن حساب المتوسط الهندسي أكثر تعقيدًا وبالتالي يصعب تفسير أهميته الإحصائية.
وباختصار فإن المتوسط الهندسي له مميزات وعيوب مقارنة بالمتوسط الحسابي، وبحسب طبيعة البيانات سيكون من المناسب حساب هذا المتوسط أو ذاك.
كيفية حساب الوسط الهندسي
لحساب الوسط الهندسي يجب تنفيذ الخطوات التالية:
- حساب منتج جميع البيانات الإحصائية في العينة.
- أوجد الجذر النوني للمنتج المحسوب.
- والنتيجة التي تم الحصول عليها هي الوسط الهندسي للعينة الإحصائية.
كما ترون، فإن إيجاد الوسط الهندسي لمجموعة من البيانات أمر بسيط نسبيًا باستخدام الآلة الحاسبة أو برنامج الكمبيوتر، حيث أنك تحتاج فقط إلى حساب حاصل الضرب والجذر. على العكس من ذلك، فإن إجراء الحساب يدويًا أمر شاق جدًا.
👉 ولهذا السبب نوصي باستخدام الآلة الحاسبة أدناه لحساب المتوسط الهندسي لمجموعة البيانات.
مثال على المتوسط الهندسي
بمجرد أن نتعرف على النظرية المتعلقة بالوسط الهندسي، سنضرب مثالًا حتى تتمكن من رؤية كيفية الحصول على المتوسط الهندسي بالضبط.
- النتائج الاقتصادية للشركة خلال السنوات الخمس الماضية معروفة. حققت الشركة في السنة الأولى ربحية اقتصادية 10%، وفي السنة الثانية وصل الربح إلى 23%، وفي السنة الثالثة بلغت الأموال المكتسبة 16%، وفي السنة الرابعة حققت ربحية اقتصادية 7% والاستثمار في السنة الخامسة يمثل عائدا قدره 20٪. يطلب منك حساب متوسط جميع النسب المئوية.
كما رأينا، لحساب متوسط النسب المئوية، لا ينبغي عليك استخدام المتوسط الحسابي، بل قم بإجراء الحساب باستخدام المتوسط الهندسي.
لذلك، نطبق صيغة الوسط الهندسي:
![]()
ونستبدل قيم المثال في الصيغة ونجري الحساب:
![]()
لاحظ أن لدينا خمس نقاط بيانات، لذا فإننا نحسب الجذر الخامس.
والنتيجة العددية للمتوسط الهندسي هي 1.15، مما يعني أن الشركة شهدت نمواً اقتصادياً بمعدل 15% في المتوسط كل عام.
ضع في اعتبارك أننا تمكنا من الحصول على الوسط الهندسي لأن جميع القيم كانت موجبة، ولكن إذا كانت أي نسبة مئوية سالبة لكان علينا وضع البيانات في الصيغة ككسر عشري موجب مع الجزء الصحيح. يساوي الصفر. على سبيل المثال، يجب التعبير عن النمو بنسبة -30% في الصيغة بـ 0.70 (1-0.3=0.7).
حاسبة المتوسط الهندسي
أدخل أي عينة إحصائية في الآلة الحاسبة أدناه للعثور على وسطها الهندسي. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري. تذكر أنه لا يمكنك تحديد الوسط الهندسي إذا كانت القيمة سالبة أو صفرًا.
خصائص الوسط الهندسي
يتميز الوسط الهندسي بالخصائص التالية:
- هذا نوع من المتوسطات مفيد جدًا للعثور على متوسط النسب المئوية أو المؤشرات.
- ولا يمكن حسابه إلا إذا كانت جميع البيانات إيجابية.
- المعنى الهندسي للوسط الهندسي لعددين a و b هو ضلع مربع له نفس مساحة المستطيل الذي قياس أضلاعه a و b .
![]()
- المعنى الهندسي للمتوسط الهندسي لثلاثة أرقام أ ، ب ، ج هو جانب المكعب الذي حجمه يعادل متوازي الأضلاع أ ، ب ، ج .
![]()
- لوغاريتم الوسط الهندسي لمجموعة من البيانات يعطي الوسط الحسابي للوغاريتمات لنفس المجموعة.
- سيكون المتوسط الهندسي لمجموعة القيم دائمًا أقل من أو يساوي الوسط الحسابي.
![]()
- يتم حساب المتوسط الهندسي المرجح بنفس طريقة المتوسط الهندسي، ولكن عن طريق إضافة أوزان إلى أس كل عنصر بيانات لترجيح القيم الإحصائية.
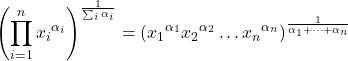
حساب الوسط الهندسي في برنامج Excel
وأخيرًا، دعونا نرى كيفية إيجاد الوسط الهندسي لمجموعة بيانات باستخدام برنامج Excel.
لحساب المتوسط الهندسي في Excel، تحتاج إلى استخدام الدالة MEANS.GEOM. ما عليك سوى إدخال جميع القيم التي تريد أخذ المتوسط الهندسي لها وستعيد الدالة نتيجة المتوسط الهندسي.
على سبيل المثال، لتحديد المتوسط الهندسي للمثال المذكور أعلاه، يجب عليك الكتابة في مربع Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) .
يجب أن تضع في اعتبارك أنه إذا كانت أي من القيم صفرًا أو سالبة، فسترجع الدالة خطأً.
كما ترون، يعد حساب المتوسط الهندسي باستخدام برنامج Excel أسهل وأسرع بكثير، حيث أنك تحتاج فقط إلى نسخ البيانات على ورقة واستخدام الصيغة.