ما هي إحصائية الاختبار الموحدة؟
الفرضية الإحصائية هي افتراض حول المعلمة السكانية . على سبيل المثال، يمكننا أن نفترض أن متوسط طول الرجل في الولايات المتحدة هو 70 بوصة. الفرضية المتعلقة بالطول هي فرضية إحصائية ومتوسط الطول الحقيقي للرجل في الولايات المتحدة هو المعلمة السكانية .
اختبار الفرضية هو اختبار إحصائي رسمي نستخدمه لرفض أو الفشل في رفض فرضية إحصائية.
العملية الأساسية لإجراء اختبار الفرضيات هي كما يلي:
1. جمع بيانات العينة.
2. حساب إحصائية الاختبار الموحد لبيانات العينة.
3. قارن إحصائية الاختبار الموحد بالقيمة الحرجة. إذا كانت أكثر تطرفًا من القيمة الحرجة، ارفض فرضية العدم. وبخلاف ذلك، لا ترفض اختبار الفرضية الصفرية.
تختلف الصيغة التي نستخدمها لحساب إحصائية الاختبار الموحد اعتمادًا على نوع اختبار الفرضيات الذي نقوم به.
يوضح الجدول التالي الصيغة المستخدمة لحساب إحصائية الاختبار الموحدة لكل نوع من الأنواع الأربعة الرئيسية لاختبار الفرضيات:
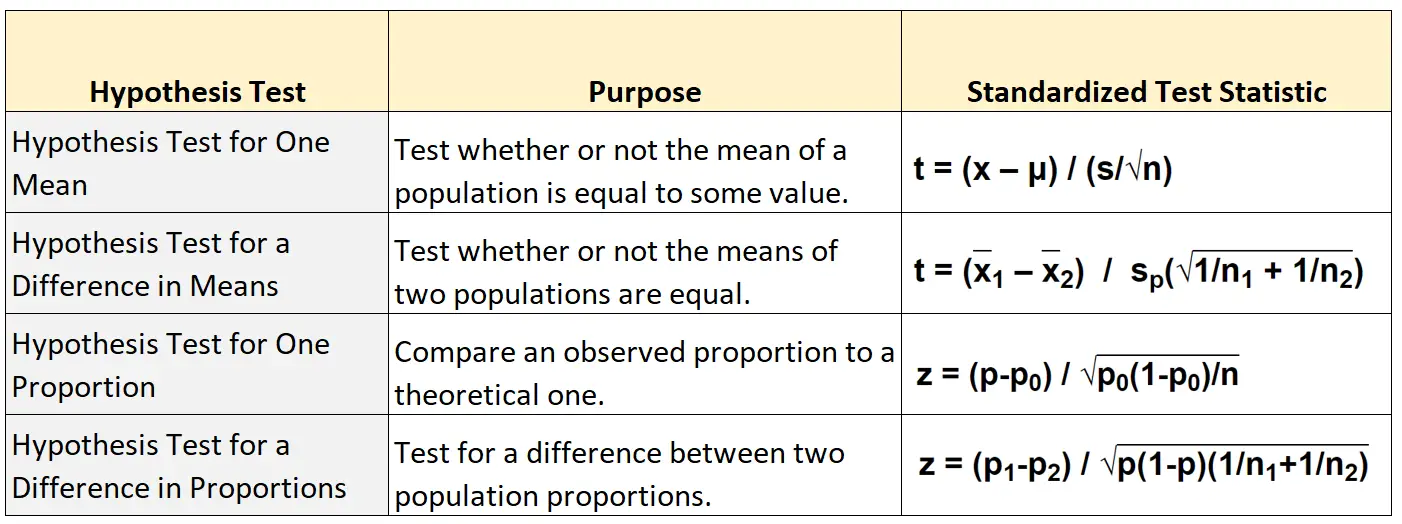
اختبار الفرضيات للمتوسط
يتم استخدام اختبار t لعينة واحدة لاختبار ما إذا كان متوسط المجتمع يساوي قيمة معينة أم لا.
ويتم حساب إحصائية الاختبار الموحد لهذا النوع من الاختبارات على النحو التالي:
ر = ( X – μ) / (ق/√ن)
ذهب:
- x: وسائل العينة
- μ 0 : متوسط عدد السكان الافتراضي
- s: عينة الانحراف المعياري
- ن: حجم العينة
ارجع إلى هذا البرنامج التعليمي للحصول على مثال لحساب إحصائية الاختبار الموحدة.
اختبار الفرضيات لاختلاف الوسائل
يتم استخدام اختبار t المكون من عينتين لاختبار ما إذا كانت متوسطات مجتمعين متساويتين أم لا.
ويتم حساب إحصائية الاختبار الموحد لهذا النوع من الاختبارات على النحو التالي:
ر = ( X 1 – X 2 ) / ث ص (√ 1/ن 1 + 1/ن 2 )
حيث x 1 وx 2 هما متوسطا العينة، وn 1 وn 2 هما حجما العينة، وحيث يتم حساب s p على النحو التالي:
ث ع = √ (ن 1 -1)ث 1 2 + (ن 2 -1)ث 2 2 / (ن 1 +ن 2 -2)
حيث s 1 2 و s 2 2 هما تباينات العينة.
ارجع إلى هذا البرنامج التعليمي للحصول على مثال لحساب إحصائية الاختبار الموحدة.
اختبار الفرضية للنسبة
يتم استخدام اختبار z ذو النسبة الواحدة لمقارنة نسبة ملحوظة مع نسبة نظرية.
ويتم حساب إحصائية الاختبار الموحد لهذا النوع من الاختبارات على النحو التالي:
ض = (ص 0 ) / √ ص 0 (1-ص 0 )/n
ذهب:
- ع: نسبة العينة المرصودة
- ع 0 : نسبة افتراضية من السكان
- ن: حجم العينة
ارجع إلى هذا البرنامج التعليمي للحصول على مثال لحساب إحصائية الاختبار الموحدة.
اختبار الفرضية للاختلاف في النسب
يتم استخدام اختبار z ثنائي النسبة لاختبار الفرق بين نسبتين سكانيتين.
ويتم حساب إحصائية الاختبار الموحد لهذا النوع من الاختبارات على النحو التالي:
ض = (ص 1 -ص 2 ) / √ ص(1-ص)(1/ن 1 +1/ن 2 )
حيث p 1 وp 2 هي نسب العينة، وn 1 وn 2 هي أحجام العينة، وحيث p هي النسبة الإجمالية المجمعة المحسوبة على النحو التالي:
ع = (ع 1 ن 1 + ص 2 ن 2 )/( ن 1 + ن 2 )
ارجع إلى هذا البرنامج التعليمي للحصول على مثال لحساب إحصائية الاختبار الموحدة.
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر