ما هو المتغير في الإحصاء؟

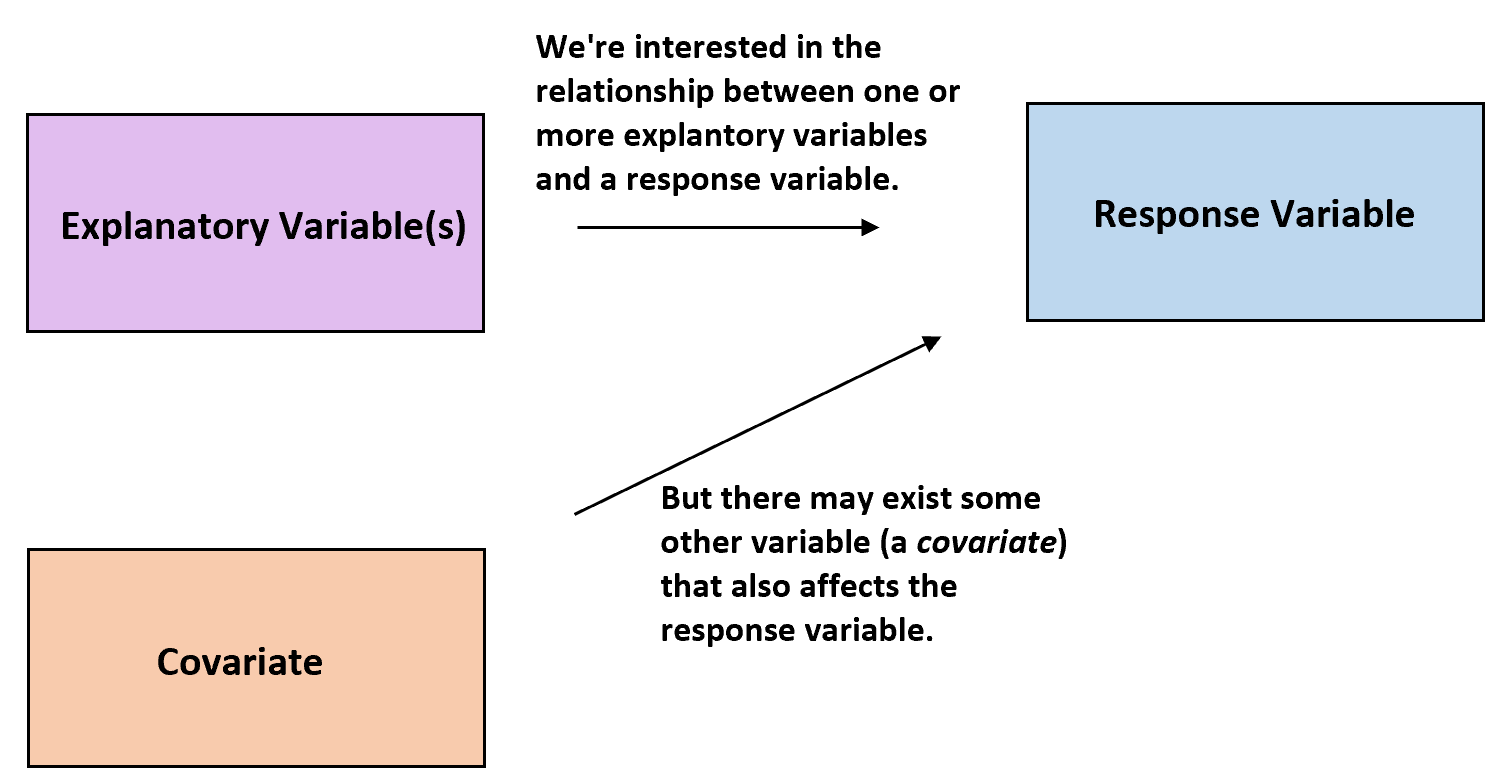
في الإحصاء، غالبًا ما يرغب الباحثون في فهم العلاقة بين واحد أو أكثر من المتغيرات التوضيحية ومتغير الاستجابة .

ومع ذلك، قد يكون الأمر أن المتغيرات الأخرى يمكن أن تؤثر على متغير الاستجابة ولا تهم الباحثين. وتسمى هذه المتغيرات المتغيرات المشتركة .

المتغيرات المشتركة: المتغيرات التي تؤثر على متغير الاستجابة، ولكنها ليست ذات أهمية في الدراسة.

على سبيل المثال، لنفترض أن الباحثين يريدون معرفة ما إذا كانت ثلاث تقنيات دراسة مختلفة تؤدي إلى متوسط درجات اختبار مختلفة في مدرسة معينة. أسلوب الدراسة هو المتغير التوضيحي ودرجة الامتحان هي متغير الاستجابة.

ومع ذلك، لا بد أن تكون هناك اختلافات في القدرات الدراسية للطلاب ضمن المجموعات الثلاث. إذا لم يؤخذ ذلك في الاعتبار، فسيكون ذلك بمثابة اختلاف غير مبرر داخل الدراسة وسيزيد من صعوبة تحديد العلاقة الحقيقية بين تقنية الدراسة ونتائج الفحص.

إحدى الطرق لحساب ذلك هي استخدام التقدير الحالي للطالب في الفصل كمتغير مشترك . من المعروف أن الدرجة الحالية للطالب من المحتمل أن تكون مرتبطة بأدائه في الامتحان في المستقبل.

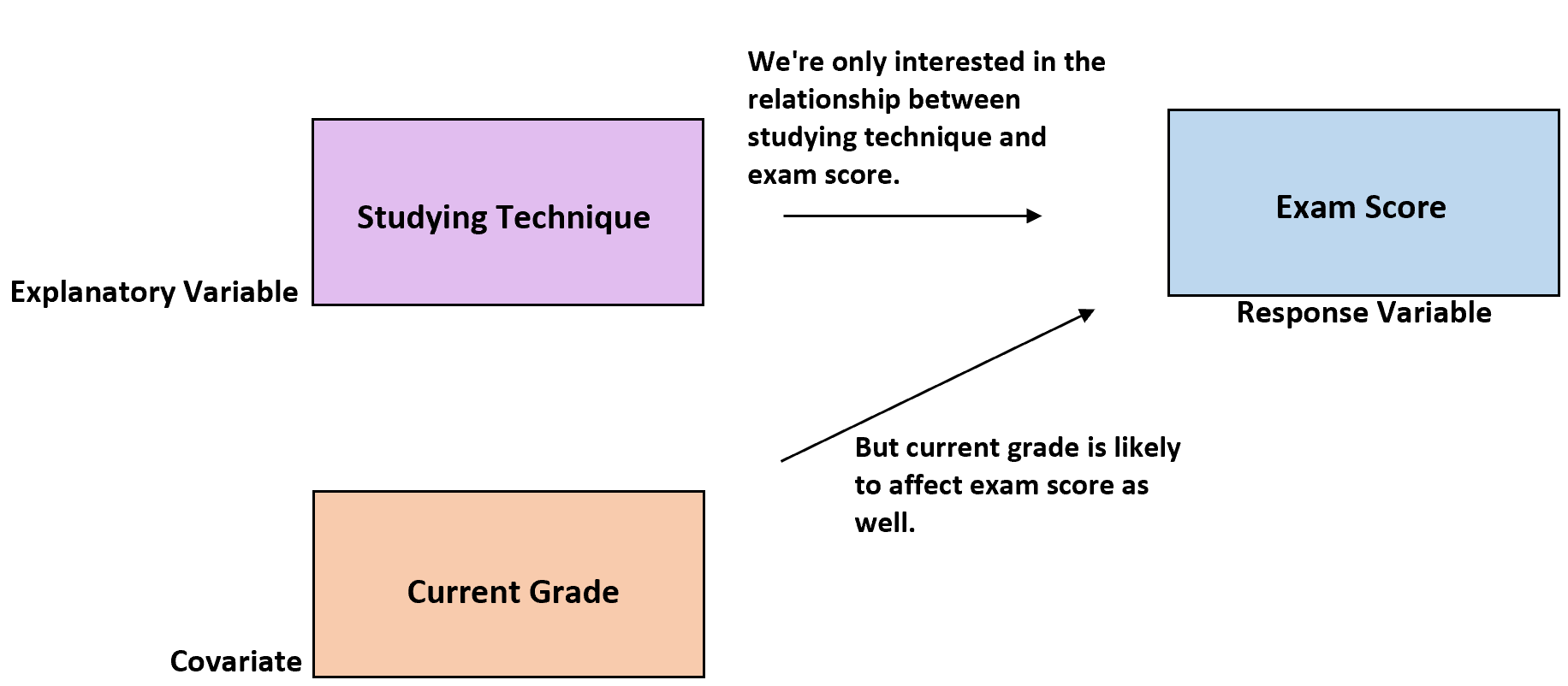
لذا، على الرغم من أن الدرجة الحالية ليست متغيرًا محل اهتمام في هذه الدراسة، إلا أنه يمكن تضمينها كمتغير مشترك حتى يتمكن الباحثون من معرفة ما إذا كانت تقنية الدراسة تؤثر على درجات الامتحانات، حتى بعد حساب الدرجة الحالية للطالب في الفصل.

تظهر المتغيرات المشتركة في أغلب الأحيان في نوعين من السياقات: ANOVA (تحليل التباين) والانحدار.

المتغيرات المشتركة في ANOVA

عندما نجري تحليل التباين (ANOVA) (سواء كان تحليل التباين أحادي الاتجاه ، أو تحليل التباين ثنائي الاتجاه ، أو أي شيء أكثر تعقيدًا)، نريد أن نعرف ما إذا كان هناك فرق بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

في مثالنا السابق، أردنا أن نفهم ما إذا كان هناك اختلاف في متوسط درجات الامتحان بين ثلاث تقنيات دراسة مختلفة أم لا. لفهم ذلك، كان بإمكاننا إجراء تحليل التباين (ANOVA) أحادي الاتجاه.

ومع ذلك، نظرًا لأننا نعلم أن الدرجة الحالية للطالب من المحتمل أيضًا أن تؤثر على درجات الامتحان، فيمكننا إدراجها كمتغير مشترك وإجراء تحليل التباين المشترك ( ANCOVA ) بدلاً من ذلك.

وهذا مشابه لتحليل التباين (ANOVA)، باستثناء أننا نقوم بتضمين متغير مستمر (الدرجة الحالية للطالب) كمتغير مشترك حتى نتمكن من فهم ما إذا كان هناك فرق في متوسط درجات الاختبار بين تقنيات التسجيل الثلاثة أم لا. الدراسة، حتى بعد الأخذ بعين الاعتبار نتائج الطالب. التصنيف الحالي .

المتغيرات المشتركة في الانحدار

عندما نقوم بإجراء الانحدار الخطي، نريد تحديد العلاقة بين واحد أو أكثر من المتغيرات التوضيحية ومتغير الاستجابة.

على سبيل المثال، يمكننا إجراء انحدار خطي بسيط لتحديد العلاقة بين اللقطات المربعة وأسعار العقارات في مدينة معينة. ومع ذلك، فمن المعروف أن عمر المنزل هو أيضًا متغير يؤثر على سعر العقارات.

وعلى وجه الخصوص، قد تكون المنازل القديمة مرتبطة بانخفاض أسعار العقارات. في هذه الحالة، سيكون عمر المنزل متغيرًا لأننا لسنا مهتمين حقًا بدراسته، ولكننا نعلم أن له تأثيرًا على أسعار المنازل.

لذلك، يمكننا تضمين عمر المنزل كمتغير توضيحي وإجراء انحدار خطي متعدد بالقدم المربع وعمر المنزل كمتغيرين توضيحيين وسعر المنزل كمتغير الاستجابة.

لذا فإن معامل الانحدار للقدم المربع سيخبرنا بمتوسط التغير في سعر المنزل المرتبط بزيادة وحدة واحدة في القدم المربع بعد حساب عمر المنزل .

مصادر إضافية

مقدمة إلى تحليل التباين (ANCOVA)
كيفية تفسير معاملات الانحدار
كيفية إجراء تحليل التباين (ANCOVA) في Excel
كيفية إجراء الانحدار الخطي المتعدد في إكسيل