كيفية تحويل البيانات إلى لغة r (السجل، الجذر التربيعي، الجذر التكعيبي)

تفترض العديد من الاختبارات الإحصائية أن بقايا متغير الاستجابة يتم توزيعها بشكل طبيعي.

ومع ذلك، فإن البقايا لا يتم توزيعها بشكل طبيعي في كثير من الأحيان. إحدى طرق حل هذه المشكلة هي تحويل متغير الاستجابة باستخدام أحد التحويلات الثلاثة:

1. تحويل السجل: تحويل متغير الاستجابة من y إلى log(y) .

2. تحويل الجذر التربيعي: تحويل متغير الاستجابة من y إلى √y .

3. تحويل الجذر التكعيبي: تحويل متغير الاستجابة من y إلى y ^1/3 .

ومن خلال إجراء هذه التحويلات، يقترب متغير الاستجابة بشكل عام من التوزيع الطبيعي. توضح الأمثلة التالية كيفية إجراء هذه التحويلات في R.

تحويل السجل في R

يوضح التعليمة البرمجية التالية كيفية إجراء تحويل السجل على متغير استجابة:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

يوضح التعليمة البرمجية التالية كيفية إنشاء رسوم بيانية لعرض توزيع y قبل وبعد إجراء تحويل السجل:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

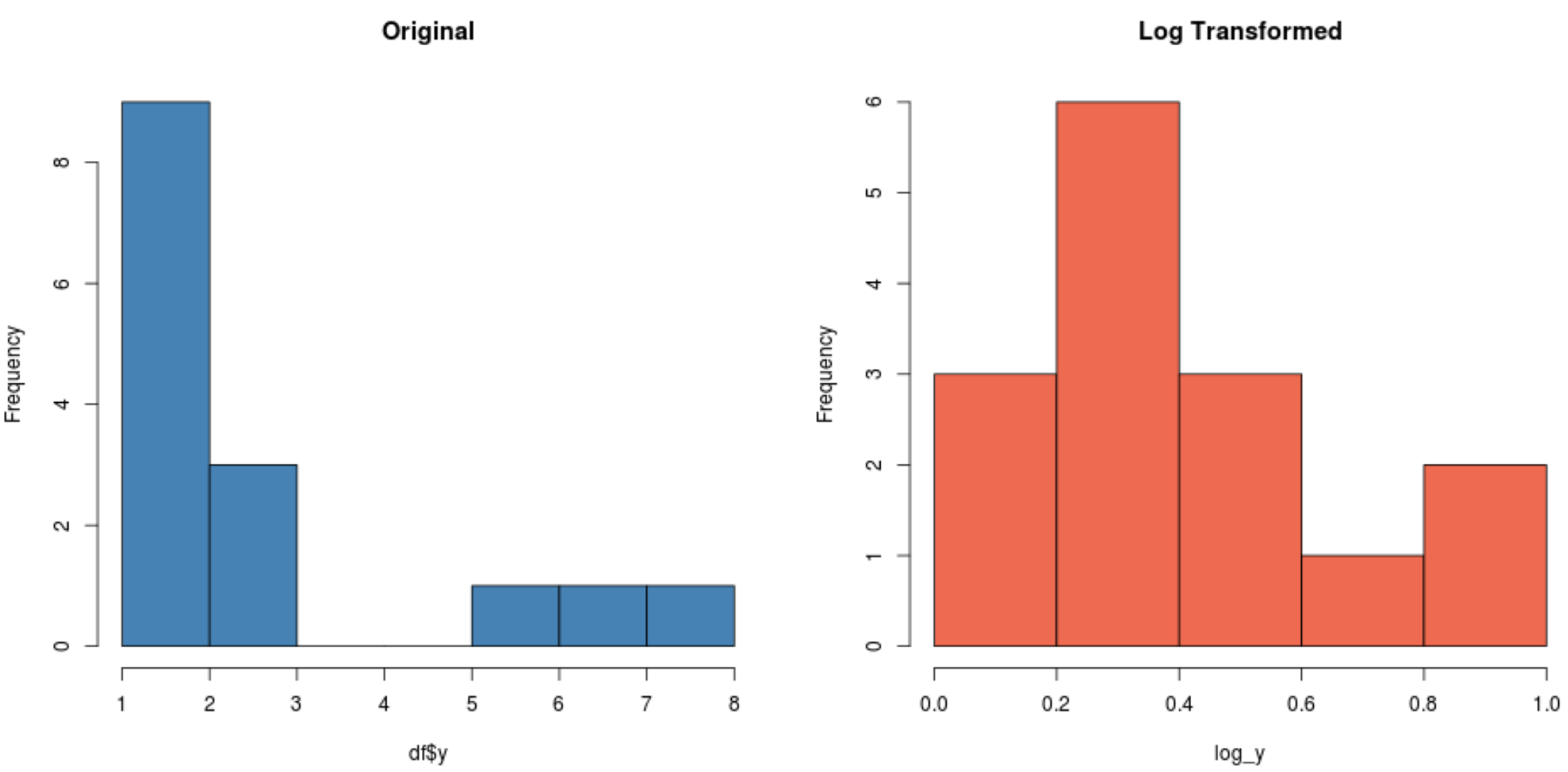
لاحظ كيف أن التوزيع المحول بالسجل أكثر طبيعية من التوزيع الأصلي. لا يزال “شكل الجرس” غير مثالي ولكنه أقرب إلى التوزيع الطبيعي من التوزيع الأصلي.

في الواقع، إذا أجرينا اختبار شابيرو-ويلك على كل توزيع، فسنجد أن التوزيع الأصلي يفشل في افتراض الحالة الطبيعية، في حين أن التوزيع المحول بالسجل لا يفشل (عند α = 0.05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

تحويل الجذر التربيعي في R

يوضح التعليمة البرمجية التالية كيفية إجراء تحويل الجذر التربيعي على متغير الاستجابة:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

يوضح التعليمة البرمجية التالية كيفية إنشاء رسوم بيانية لعرض توزيع y قبل وبعد إجراء تحويل الجذر التربيعي:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

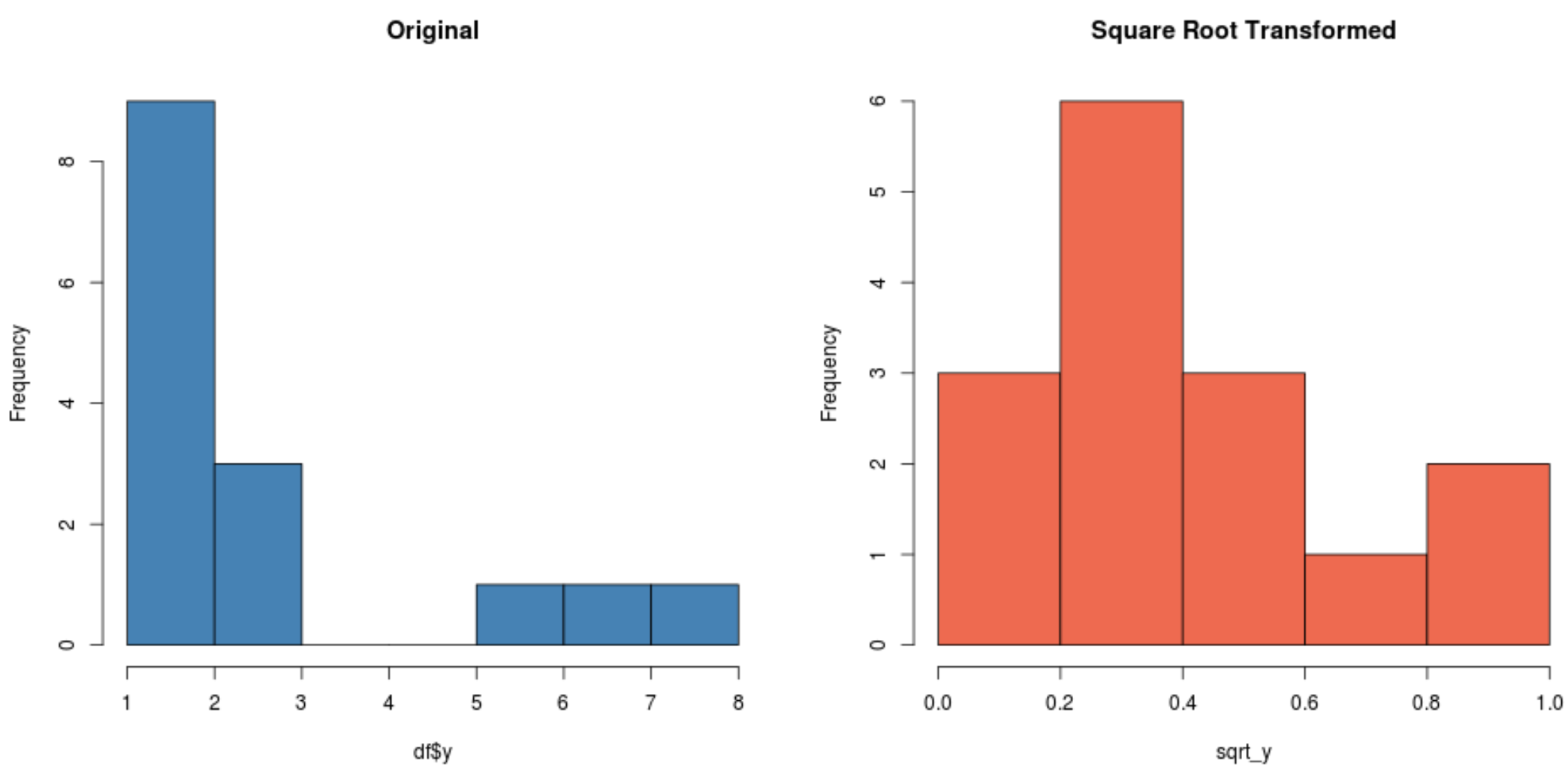
لاحظ كيف أن التوزيع المحول للجذر التربيعي يتم توزيعه بشكل طبيعي أكثر من التوزيع الأصلي.

تحويل الجذر التكعيبي في R

يوضح التعليمة البرمجية التالية كيفية إجراء تحويل الجذر التكعيبي على متغير الاستجابة:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

يوضح التعليمة البرمجية التالية كيفية إنشاء رسوم بيانية لعرض توزيع y قبل وبعد إجراء تحويل الجذر التربيعي:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

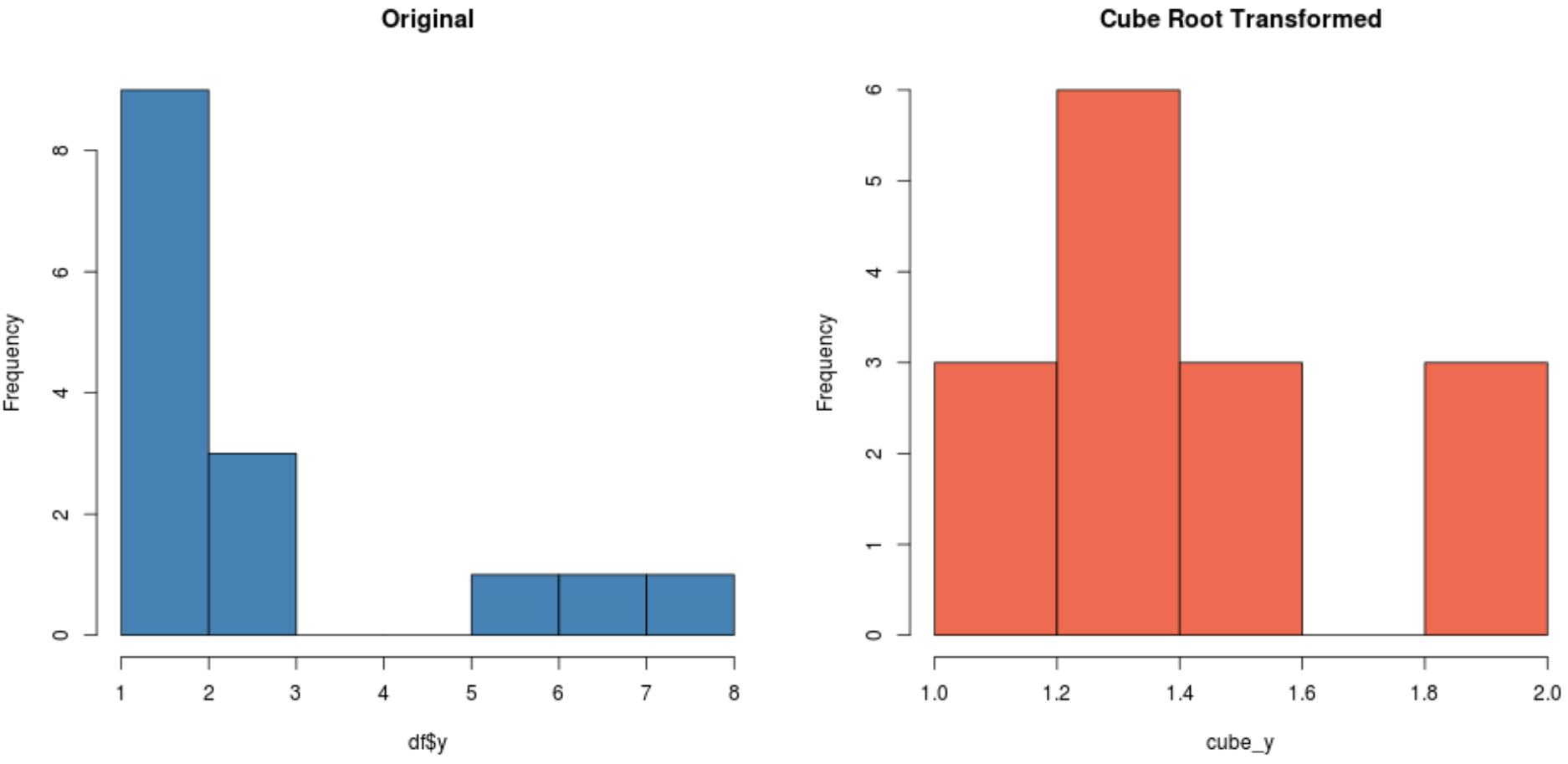
اعتمادًا على مجموعة البيانات الخاصة بك، قد ينتج عن أحد هذه التحويلات مجموعة بيانات جديدة يتم توزيعها بشكل طبيعي أكثر من غيرها.