ما هو التجهيز الزائد في التعلم الآلي؟ (شرح وأمثلة)

في التعلم الآلي، غالبًا ما نبني نماذج حتى نتمكن من إجراء تنبؤات دقيقة حول ظواهر معينة.

على سبيل المثال، لنفترض أننا نريد إنشاء نموذج انحدار يستخدم متغير التوقع للساعات التي يقضيها في الدراسة للتنبؤ بدرجة ACT الخاصة بمتغير الاستجابة لطلاب المدارس الثانوية.

لبناء هذا النموذج، سنقوم بجمع بيانات عن الساعات التي يقضيها في الدراسة ودرجة ACT المقابلة لمئات الطلاب في منطقة تعليمية معينة.

سنستخدم بعد ذلك هذه البيانات لتدريب نموذج يمكنه إجراء تنبؤات حول النتيجة التي سيحصل عليها طالب معين بناءً على إجمالي عدد الساعات المدروسة.

ولتقييم فائدة النموذج، يمكننا قياس مدى توافق تنبؤات النموذج مع البيانات المرصودة. أحد المقاييس الأكثر استخدامًا للقيام بذلك هو متوسط مربع الخطأ (MSE)، والذي يتم حسابه على النحو التالي:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

ذهب:

• ن : العدد الإجمالي للملاحظات
• y _i : قيمة الاستجابة للملاحظة ^رقم
• f( _xi ): قيمة الاستجابة المتوقعة ^{للملاحظة} i

كلما كانت تنبؤات النموذج أقرب إلى الملاحظات، كلما انخفض MSE.

ومع ذلك، فإن أحد أكبر الأخطاء التي تم ارتكابها في التعلم الآلي هو تحسين النماذج لتقليل تدريب MSE ، أي مدى مطابقة تنبؤات النموذج للبيانات التي استخدمناها لتدريب النموذج.

عندما يركز النموذج أكثر من اللازم على تقليل تدريب المشاريع الصغيرة والمتوسطة الحجم، فإنه غالبًا ما يعمل بجهد كبير للعثور على أنماط في بيانات التدريب التي تنتج ببساطة عن طريق الصدفة. وبعد ذلك، عندما يتم تطبيق النموذج على البيانات غير المرئية، يكون أدائه ضعيفًا.

تُعرف هذه الظاهرة باسم التجهيز الزائد . يحدث هذا عندما “نلائم” نموذجًا بشكل وثيق جدًا مع بيانات التدريب، وبالتالي ينتهي بنا الأمر إلى بناء نموذج غير مفيد للتنبؤ بالبيانات الجديدة.

مثال على التجهيز الزائد

لفهم التجهيز الزائد، دعنا نعود إلى مثال إنشاء نموذج انحدار يستخدم الساعات التي يقضيها في الدراسة للتنبؤ بنتيجة ACT .

لنفترض أننا نجمع بيانات لـ 100 طالب في منطقة تعليمية معينة وننشئ مخططًا مبعثرًا سريعًا لتصور العلاقة بين المتغيرين:

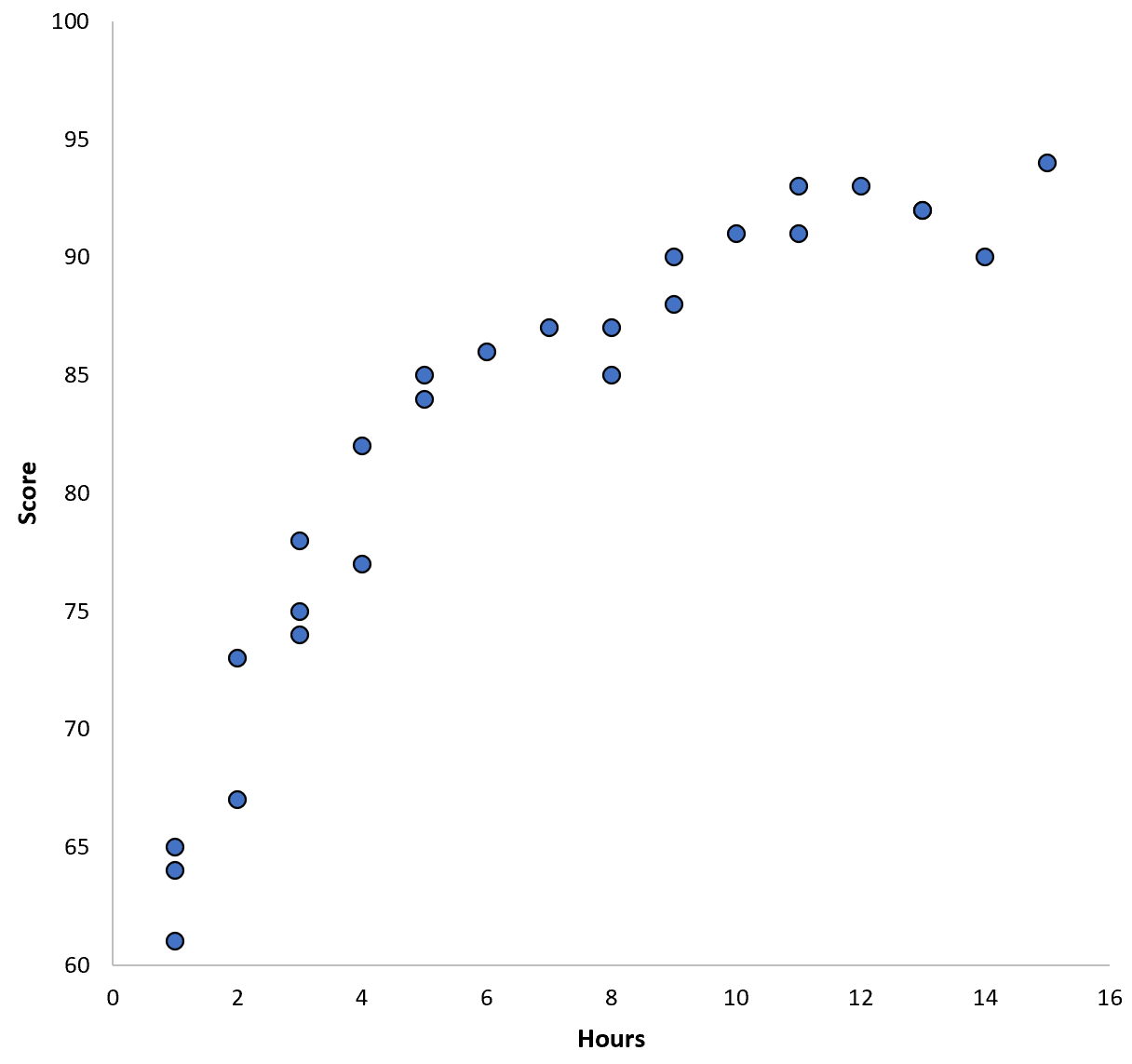
تبدو العلاقة بين المتغيرين علاقة تربيعية، لذا لنفترض أننا طبقنا نموذج الانحدار التربيعي التالي:

النتيجة = 60.1 + 5.4*(ساعات) – 0.2*(ساعات) ²

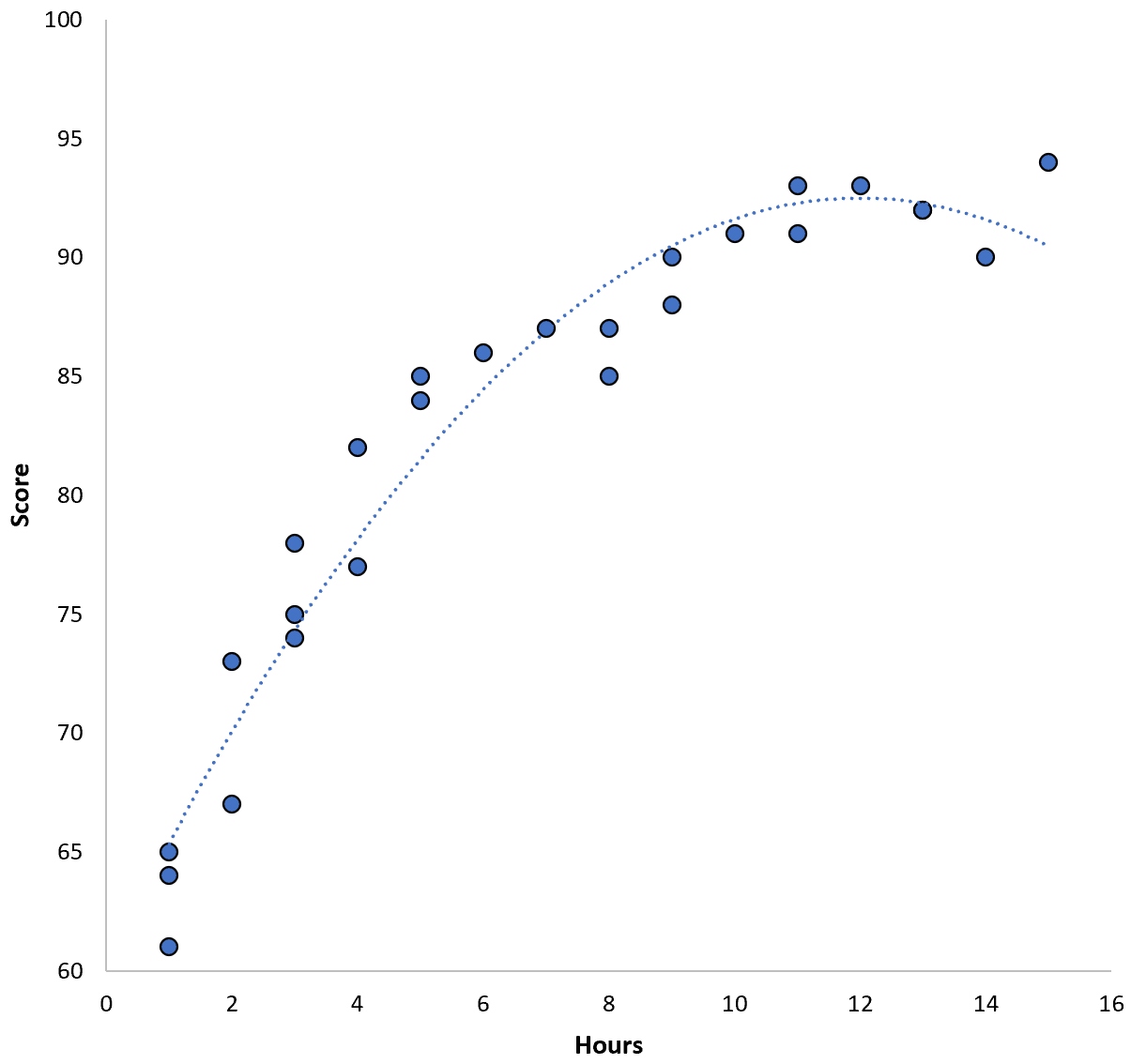
يحتوي هذا النموذج على متوسط خطأ مربع تدريبي (MSE) قدره 3.45 . أي أن جذر متوسط مربع الفرق بين التنبؤات التي قدمها النموذج ودرجات ACT الفعلية هو 3.45.

ومع ذلك، يمكننا تقليل هذا التدريب MSE من خلال تركيب نموذج متعدد الحدود ذو رتبة أعلى. على سبيل المثال، لنفترض أننا نطبق النموذج التالي:

النتيجة = 64.3 – 7.1*(ساعات) + 8.1*(ساعات) ² – 2.1*(ساعات) ³ + 0.2*(ساعات ^{) 4 – 0.1*(ساعات) 5 +} 0.2(ساعات) ⁶

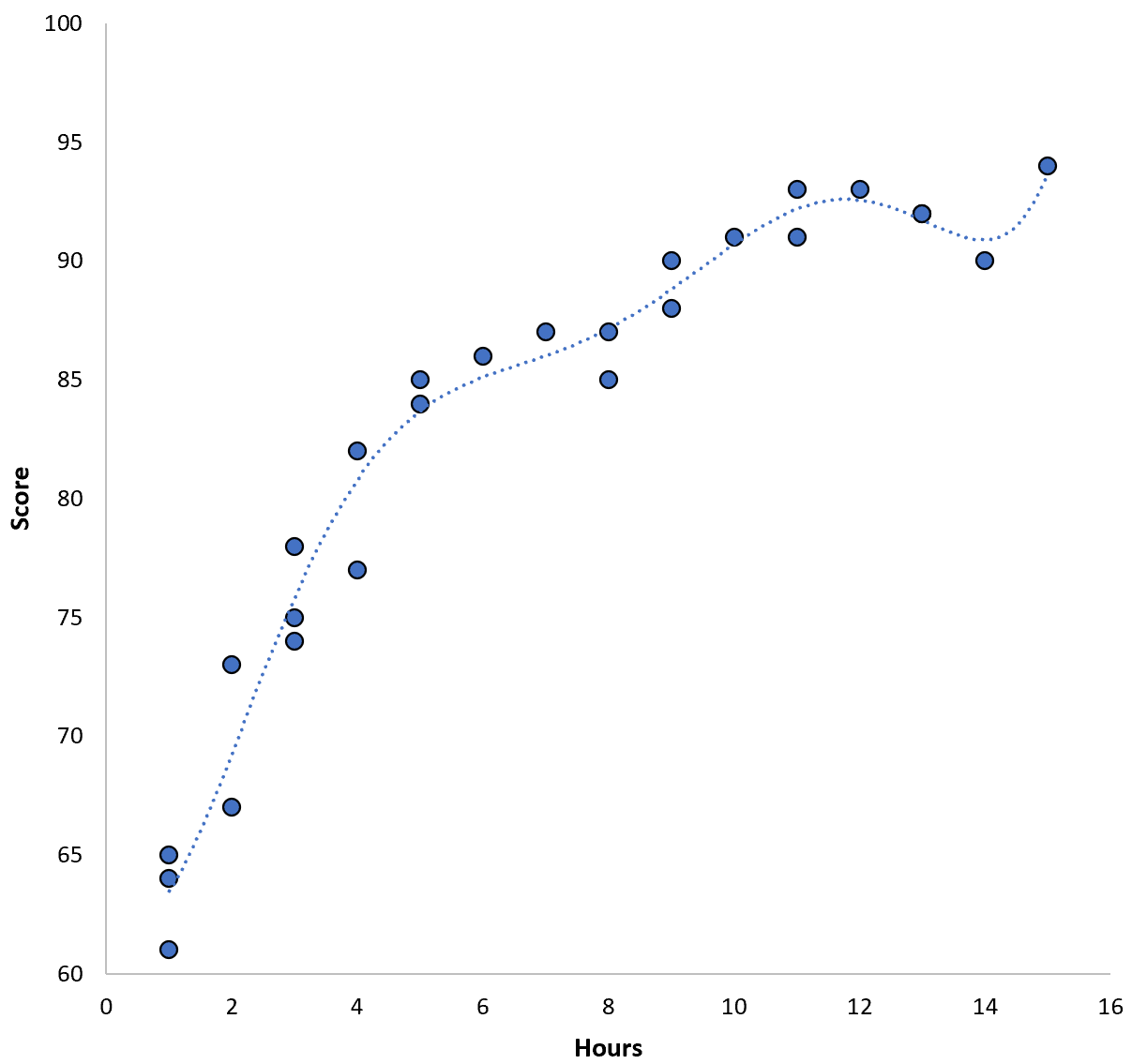
لاحظ كيف يتناسب خط الانحدار مع البيانات الفعلية بشكل أقرب بكثير من خط الانحدار السابق.

يحتوي هذا النموذج على جذر تدريب لمتوسط الخطأ التربيعي (MSE) يبلغ 0.89 فقط. أي أن جذر متوسط مربع الفرق بين التنبؤات التي قدمها النموذج ودرجات ACT الفعلية هو 0.89.

إن تدريب MSE هذا أصغر بكثير من ذلك الذي أنتجه النموذج السابق.

ومع ذلك، نحن لا نهتم حقًا بتدريب MSE ، أي مدى تطابق تنبؤات النموذج مع البيانات التي استخدمناها لتدريب النموذج. وبدلاً من ذلك، نحن نهتم بشكل أساسي باختبار MSE – وهو اختبار MSE عندما يتم تطبيق نموذجنا على البيانات غير المرئية.

إذا طبقنا نموذج الانحدار متعدد الحدود ذو الترتيب الأعلى أعلاه على مجموعة بيانات غير مرئية، فمن المحتمل أن يكون أداؤه أسوأ من نموذج الانحدار التربيعي الأبسط. وهذا يعني أنه سيؤدي إلى اختبار MSE أعلى، وهو بالضبط ما لا نريده.

كيفية اكتشاف وتجنب التجهيز الزائد

إن أبسط طريقة لاكتشاف التجهيز الزائد هي إجراء التحقق المتبادل. تُعرف الطريقة الأكثر استخدامًا بالتحقق المتقاطع k-fold وتعمل على النحو التالي:

الخطوة 1: قم بتقسيم مجموعة البيانات عشوائيًا إلى مجموعات k ، أو “طيات”، ذات حجم متساوٍ تقريبًا.

الخطوة 2: اختر إحدى الطيات لتكون مجموعة التثبيت الخاصة بك. اضبط القالب على طيات k-1 المتبقية. حساب اختبار MSE على الملاحظات في الطبقة التي تم شدها.

الخطوة 3: كرر هذه العملية عدة مرات، في كل مرة باستخدام مجموعة مختلفة كمجموعة الاستبعاد.

الخطوة 4: احسب إجمالي MSE للاختبار كمتوسط k MSE للاختبار.

اختبار MSE = (1/ك)*ΣMSE _ط

ذهب:

• ك: عدد الطيات
• MSE _i : اختبار MSE في التكرار ^الأول

يمنحنا اختبار MSE هذا فكرة جيدة عن كيفية أداء نموذج معين على البيانات غير المعروفة.

من الناحية العملية، يمكننا أن نلائم العديد من النماذج المختلفة ونقوم بإجراء التحقق المتبادل من k-fold على كل نموذج لمعرفة اختبار MSE الخاص به. يمكننا بعد ذلك اختيار النموذج ذو أدنى اختبار MSE باعتباره أفضل نموذج لاستخدامه في التنبؤ بالمستقبل.

وهذا يضمن أننا نختار النموذج الذي من المرجح أن يحقق أفضل أداء على البيانات المستقبلية، على عكس النموذج الذي يقلل ببساطة من تدريب الشركات الصغيرة والمتوسطة و”يناسب” بشكل جيد مع البيانات التاريخية.

مصادر إضافية

ما هي مقايضة التحيز والتباين في التعلم الآلي؟
مقدمة للتحقق من صحة K-Fold
نماذج الانحدار والتصنيف في التعلم الآلي