المربعات الصغرى الجزئية في r (خطوة بخطوة)

إحدى المشاكل الأكثر شيوعًا التي ستواجهها في التعلم الآلي هي تعدد الخطية . يحدث هذا عندما يكون هناك ارتباط كبير بين متغيرين أو أكثر من متغيرات التوقع في مجموعة البيانات.

عندما يحدث ذلك، قد يكون النموذج قادرًا على ملاءمة مجموعة بيانات التدريب بشكل جيد، ولكنه قد يكون أداؤه ضعيفًا على مجموعة بيانات جديدة لم يسبق له رؤيتها لأنها تتفوق على مجموعة بيانات التدريب. عدة التدريبات.

إحدى الطرق للتغلب على هذه المشكلة هي استخدام طريقة تسمى المربعات الصغرى الجزئية ، والتي تعمل على النحو التالي:

• توحيد متغيرات التوقع والاستجابة.
• حساب مجموعات خطية M (تسمى “مكونات PLS”) من متغيرات التوقع الأصلية p التي تشرح قدرًا كبيرًا من التباين في كل من متغير الاستجابة ومتغيرات التوقع.
• استخدم طريقة المربعات الصغرى لملاءمة نموذج الانحدار الخطي باستخدام مكونات PLS كمتنبئات.
• استخدم التحقق المتقاطع k-fold للعثور على العدد الأمثل لمكونات PLS للاحتفاظ بها في النموذج.

يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية تنفيذ المربعات الصغرى الجزئية في R.

الخطوة 1: تحميل الحزم اللازمة

أسهل طريقة لإجراء المربعات الصغرى الجزئية في R هي استخدام الوظائف الموجودة في الحزمة pls .

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

الخطوة 2: ملاءمة نموذج المربعات الصغرى الجزئية

في هذا المثال، سوف نستخدم مجموعة بيانات R المضمنة والتي تسمى mtcars والتي تحتوي على بيانات عن أنواع مختلفة من السيارات:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

في هذا المثال، سوف نقوم بتركيب نموذج المربعات الصغرى الجزئية (PLS) باستخدام hp كمتغير الاستجابة والمتغيرات التالية كمتغيرات متوقعة:

• ميلا في الغالون
• عرض
• القرف
• وزن
• com.qsec

يوضح الكود التالي كيفية ملاءمة نموذج PLS لهذه البيانات. لاحظ الحجج التالية:

• مقياس = TRUE : هذا يخبر R بأن كل متغير من المتغيرات في مجموعة البيانات يجب أن يتم قياسه ليكون متوسطه 0 وانحراف معياري قدره 1. وهذا يضمن عدم وجود متغير متنبئ له تأثير كبير في النموذج إذا تم قياسه بوحدات مختلفة.
• validation=”CV” : هذا يخبر R باستخدام التحقق المتقاطع k-fold لتقييم أداء النموذج. لاحظ أن هذا يستخدم k=10 طيات بشكل افتراضي. لاحظ أيضًا أنه يمكنك تحديد “LOOCV” بدلاً من ذلك لإجراء التحقق من صحة الإجازة الواحدة .

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

الخطوة 3: اختر عدد مكونات PLS

بمجرد أن نجهز النموذج، نحتاج إلى تحديد عدد مكونات PLS التي يجب الاحتفاظ بها.

للقيام بذلك، ما عليك سوى إلقاء نظرة على اختبار جذر متوسط مربع الخطأ (اختبار RMSE) المحسوب عن طريق التحقق من صحة k-cross:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03

هناك جدولان مثيران للاهتمام في النتيجة:

1. التحقق من الصحة: RMSEP

يخبرنا هذا الجدول باختبار RMSE المحسوب عن طريق التحقق من صحة k-fold. يمكننا أن نرى ما يلي:

• إذا استخدمنا المصطلح الأصلي فقط في النموذج، فإن قيمة RMSE للاختبار هي 69.66 .
• إذا أضفنا مكون PLS الأول، ينخفض اختبار RMSE إلى 40.57.
• إذا أضفنا مكون PLS الثاني، فإن اختبار RMSE ينخفض إلى 35.48.

يمكننا أن نرى أن إضافة مكونات PLS إضافية يؤدي في الواقع إلى زيادة في RMSE للاختبار. وبالتالي، يبدو أنه سيكون من الأمثل استخدام مكونين PLS فقط في النموذج النهائي.

2. التدريب: شرح نسبة التباين

يوضح لنا هذا الجدول نسبة التباين في متغير الاستجابة الموضح بمكونات PLS. يمكننا أن نرى ما يلي:

• باستخدام مكون PLS الأول فقط، يمكننا تفسير 68.66% من التباين في متغير الاستجابة.
• وبإضافة مكون PLS الثاني يمكننا تفسير 89.27% من التباين في متغير الاستجابة.

لاحظ أننا سنظل قادرين على تفسير المزيد من التباين باستخدام المزيد من مكونات PLS، ولكن يمكننا أن نرى أن إضافة أكثر من مكونين PLS لا يؤدي في الواقع إلى زيادة نسبة التباين الموضح كثيرًا.

يمكننا أيضًا تصور اختبار RMSE (جنبًا إلى جنب مع اختبار MSE واختبار R-squared) كدالة لعدد مكونات PLS باستخدام وظيفة validationplot() .

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type=" MSEP ")
validationplot(model, val.type=" R2 ") 

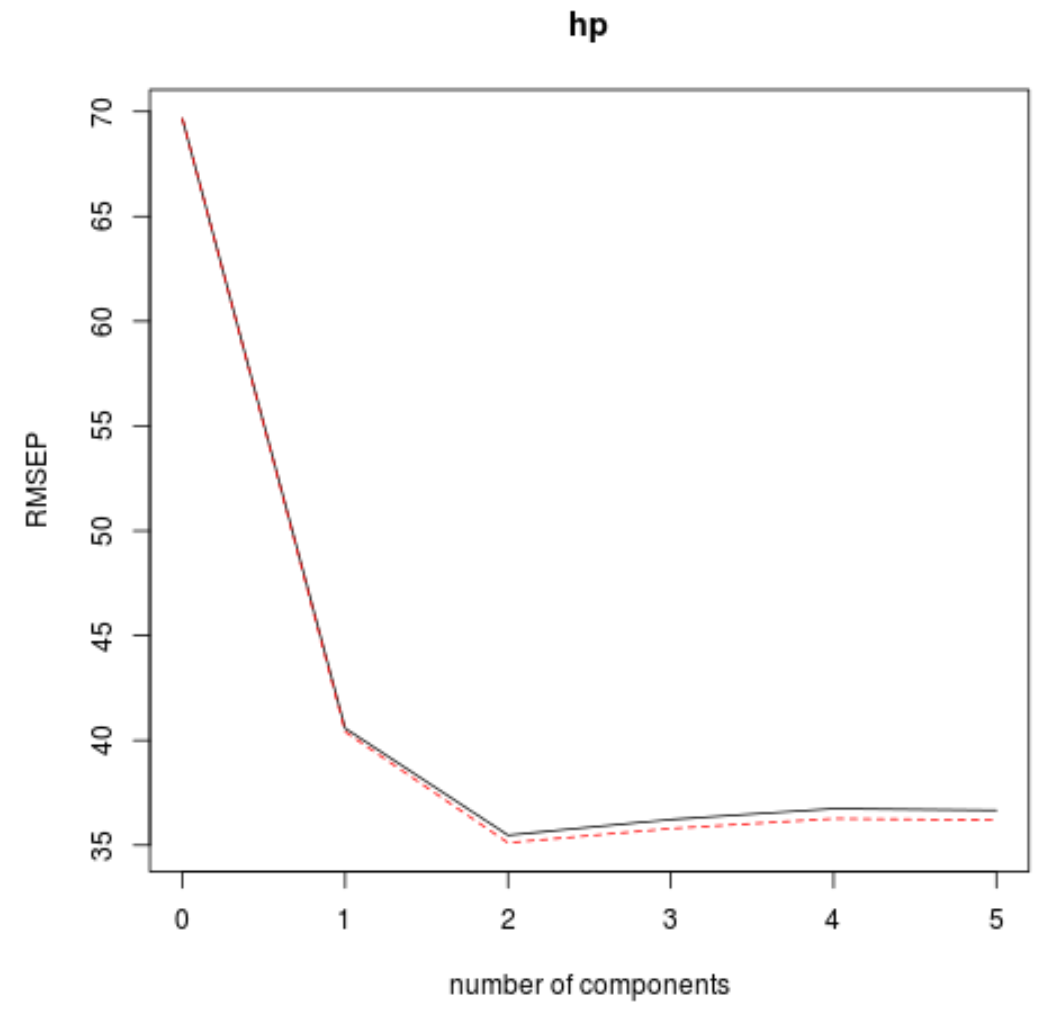
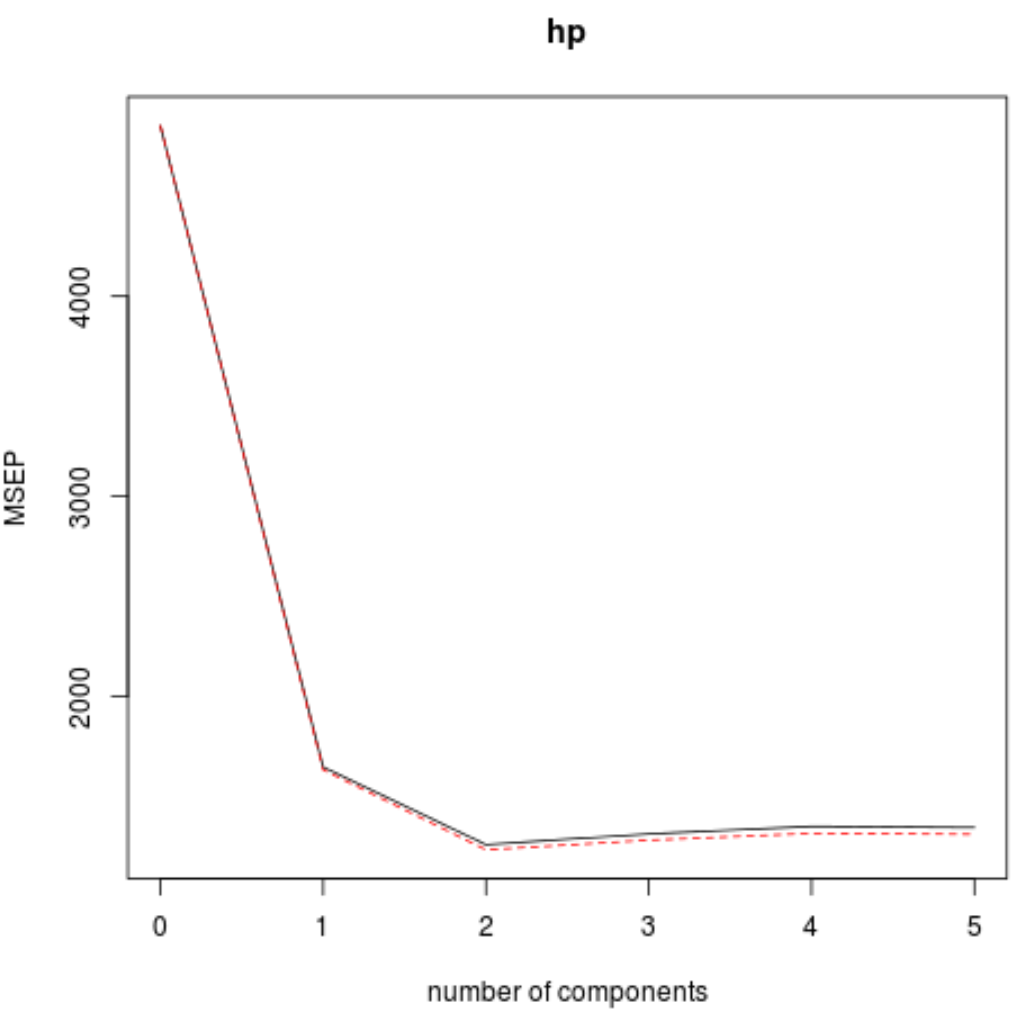
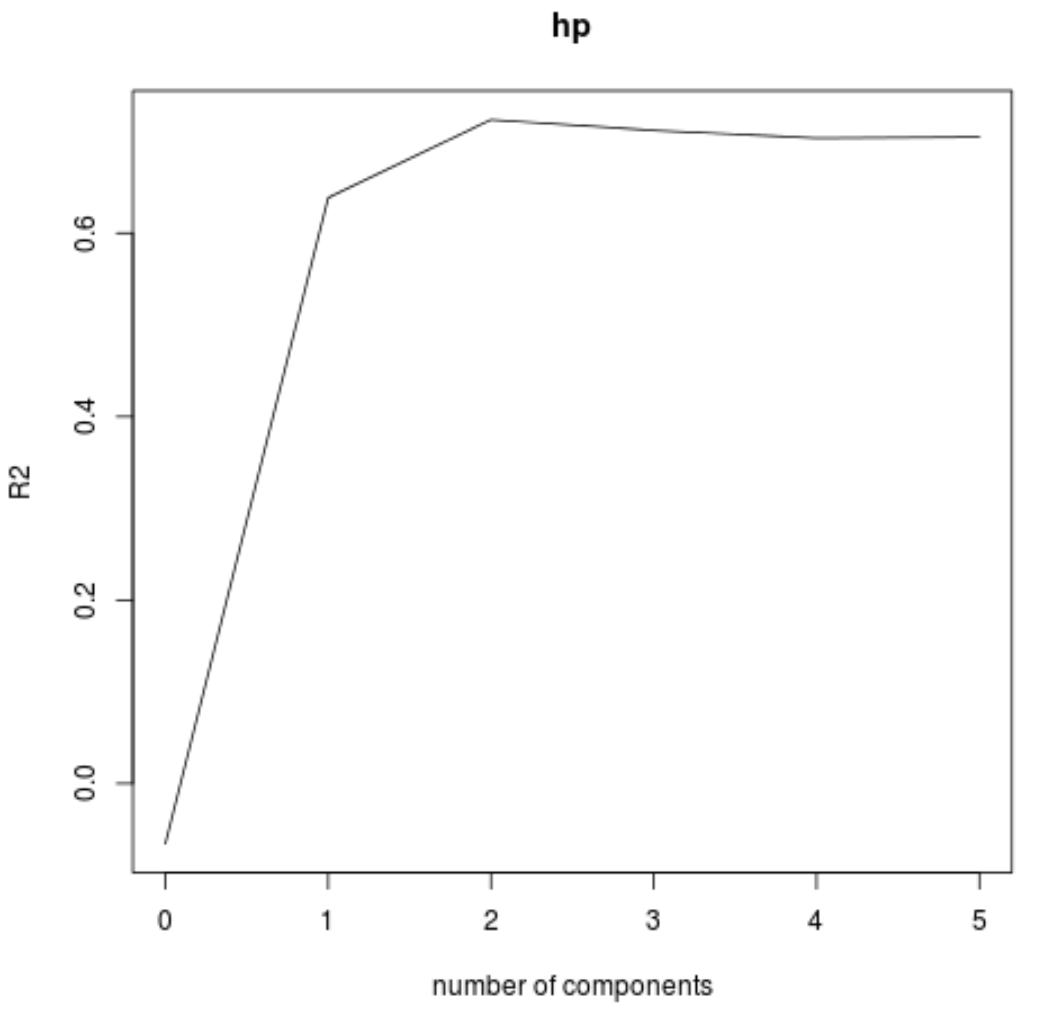
في كل رسم بياني، يمكننا أن نرى أن ملاءمة النموذج تتحسن عن طريق إضافة مكونين PLS، ولكنه يميل إلى التدهور عندما نضيف المزيد من مكونات PLS.

وبالتالي، فإن النموذج الأمثل يتضمن فقط أول مكونين من مكونات PLS.

الخطوة 4: استخدم النموذج النهائي لعمل تنبؤات

يمكننا استخدام النموذج النهائي مع مكونين PLS لعمل تنبؤات حول الملاحظات الجديدة.

يوضح الكود التالي كيفية تقسيم مجموعة البيانات الأصلية إلى مجموعة تدريب واختبار واستخدام النموذج النهائي مع مكوني PLS لعمل تنبؤات على مجموعة الاختبار.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 54.89609

نرى أن RMSE للاختبار تبين أنه 54.89609 . هذا هو متوسط الانحراف بين قيمة حصان المتوقعة وقيمة حصان المرصودة لملاحظات مجموعة الاختبار.

لاحظ أن نموذج انحدار المكونات الرئيسية المكافئ مع مكونين رئيسيين أنتج اختبار RMSE قدره 56.86549 . وهكذا، تفوق نموذج PLS قليلاً على نموذج PCR لمجموعة البيانات هذه.

يمكن العثور هنا على الاستخدام الكامل لرمز R في هذا المثال.