المربعات الصغرى الجزئية في بايثون (خطوة بخطوة)

إحدى المشاكل الأكثر شيوعًا التي ستواجهها في التعلم الآلي هي تعدد الخطية . يحدث هذا عندما يكون هناك ارتباط كبير بين متغيرين أو أكثر من متغيرات التوقع في مجموعة البيانات.

عندما يحدث ذلك، قد يكون النموذج قادرًا على ملاءمة مجموعة بيانات التدريب بشكل جيد، ولكنه قد يكون أداؤه ضعيفًا على مجموعة بيانات جديدة لم يسبق له رؤيتها لأنها تتفوق على مجموعة بيانات التدريب. عدة التدريبات.

إحدى الطرق للتغلب على هذه المشكلة هي استخدام طريقة تسمى المربعات الصغرى الجزئية ، والتي تعمل على النحو التالي:

• توحيد متغيرات التوقع والاستجابة.
• حساب مجموعات خطية M (تسمى “مكونات PLS”) من متغيرات التوقع الأصلية p التي تشرح قدرًا كبيرًا من التباين في كل من متغير الاستجابة ومتغيرات التوقع.
• استخدم طريقة المربعات الصغرى لملاءمة نموذج الانحدار الخطي باستخدام مكونات PLS كمتنبئات.
• استخدم التحقق المتقاطع k-fold للعثور على العدد الأمثل لمكونات PLS للاحتفاظ بها في النموذج.

يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية تنفيذ المربعات الصغرى الجزئية في بايثون.

الخطوة 1: استيراد الحزم اللازمة

أولاً، سنقوم باستيراد الحزم اللازمة لتنفيذ المربعات الصغرى الجزئية في بايثون:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

الخطوة 2: تحميل البيانات

في هذا المثال، سنستخدم مجموعة بيانات تسمى mtcars ، والتي تحتوي على معلومات عن 33 سيارة مختلفة. سوف نستخدم hp كمتغير الاستجابة والمتغيرات التالية كتنبؤات:

• ميلا في الغالون
• عرض
• القرف
• وزن
• com.qsec

يوضح الكود التالي كيفية تحميل مجموعة البيانات هذه وعرضها:

 #define URL where data is located
url = "https://raw.githubusercontent.com/- Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

الخطوة 3: ملاءمة نموذج المربعات الصغرى الجزئية

يوضح الكود التالي كيفية ملاءمة نموذج PLS لهذه البيانات.

لاحظ أن cv = RepeatedKFold() يطلب من Python استخدام التحقق المتبادل k-fold لتقييم أداء النموذج. في هذا المثال نختار k = 10 أضعاف، تكرر 3 مرات.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

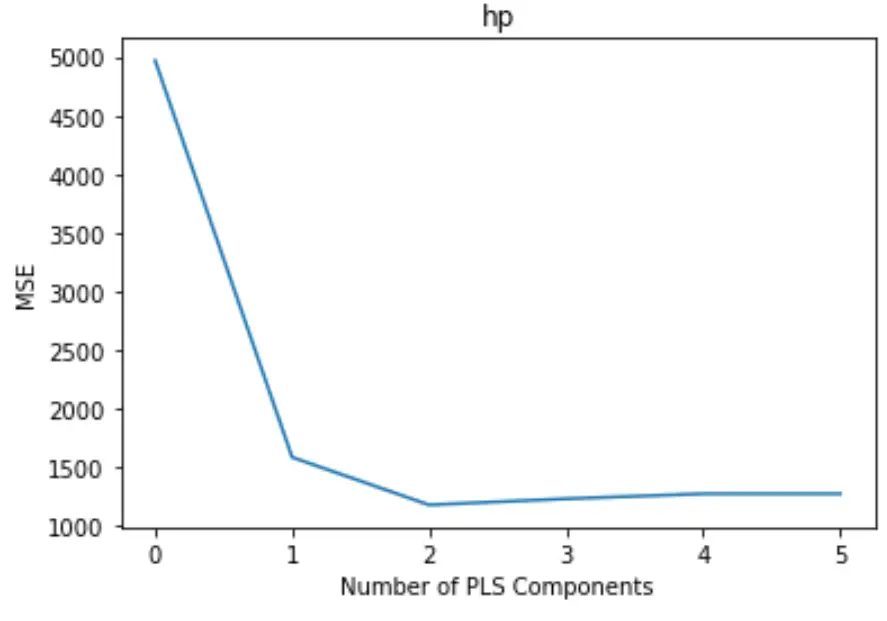
تعرض المؤامرة عدد مكونات PLS على طول المحور السيني واختبار MSE (متوسط الخطأ المربع) على طول المحور الصادي.

من الرسم البياني، يمكننا أن نرى أن MSE للاختبار يتناقص بإضافة مكونين PLS، لكنه يبدأ في الزيادة عندما نضيف أكثر من مكونين PLS.

وبالتالي، فإن النموذج الأمثل يتضمن فقط أول مكونين من مكونات PLS.

الخطوة 4: استخدم النموذج النهائي لعمل تنبؤات

يمكننا استخدام نموذج PLS النهائي مع مكونين من PLS للتنبؤ بالملاحظات الجديدة.

يوضح الكود التالي كيفية تقسيم مجموعة البيانات الأصلية إلى مجموعة تدريب واختبار واستخدام نموذج PLS مع مكونين PLS لعمل تنبؤات على مجموعة الاختبار.

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

نرى أن RMSE للاختبار تبين أنه 29.9094 . هذا هو متوسط الانحراف بين قيمة حصان المتوقعة وقيمة حصان المرصودة لملاحظات مجموعة الاختبار.

يمكن العثور على كود Python الكامل المستخدم في هذا المثال هنا .