خطوط الانحدار التكيفي متعدد المتغيرات في r

يمكن استخدام خطوط الانحدار التكيفي متعدد المتغيرات (MARS) لنمذجة العلاقات غير الخطية بين مجموعة من المتغيرات المتوقعة ومتغير الاستجابة .

تعمل هذه الطريقة على النحو التالي:

1. قم بتقسيم مجموعة البيانات إلى أجزاء k .

2. تناسب نموذج الانحدار لكل جزء.

3. استخدم التحقق المتبادل k-fold لاختيار قيمة لـ k .

يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية ملاءمة نموذج MARS لمجموعة بيانات في R.

الخطوة 1: تحميل الحزم اللازمة

في هذا المثال، سوف نستخدم مجموعة بيانات ISLR للأجور .   الحزمة التي تحتوي على الرواتب السنوية لـ 3000 شخص إلى جانب مجموعة متنوعة من المتغيرات المتوقعة مثل العمر والتعليم والعرق والمزيد.

قبل تركيب نموذج MARS على البيانات، سنقوم بتحميل الحزم اللازمة:

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

الخطوة 2: عرض البيانات

بعد ذلك، سنعرض الصفوف الستة الأولى من مجموعة البيانات التي نعمل معها:

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

الخطوة 3: إنشاء نموذج المريخ وتحسينه

بعد ذلك، سنقوم بإنشاء نموذج MARS لمجموعة البيانات هذه وإجراء التحقق المتبادل من k-fold لتحديد النموذج الذي ينتج أقل اختبار RMSE (متوسط الخطأ المربع).

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

من النتائج، يمكننا أن نرى أن النموذج الذي أنتج أدنى اختبار MSE كان نموذجًا له تأثيرات من الدرجة الأولى فقط (أي لا توجد شروط تفاعل) و12 مصطلحًا. أنتج هذا النموذج خطأ جذر متوسط مربع (RMSE) قدره 33.8164 .

ملاحظة: استخدمنا طريقة = “الأرض” لتحديد نموذج المريخ. يمكنك العثور على وثائق لهذه الطريقة هنا .

يمكننا أيضًا إنشاء مخطط لتصور اختبار RMSE بناءً على الدرجة وعدد المصطلحات:

 #display test RMSE by terms and degree
ggplot(cv_mars)

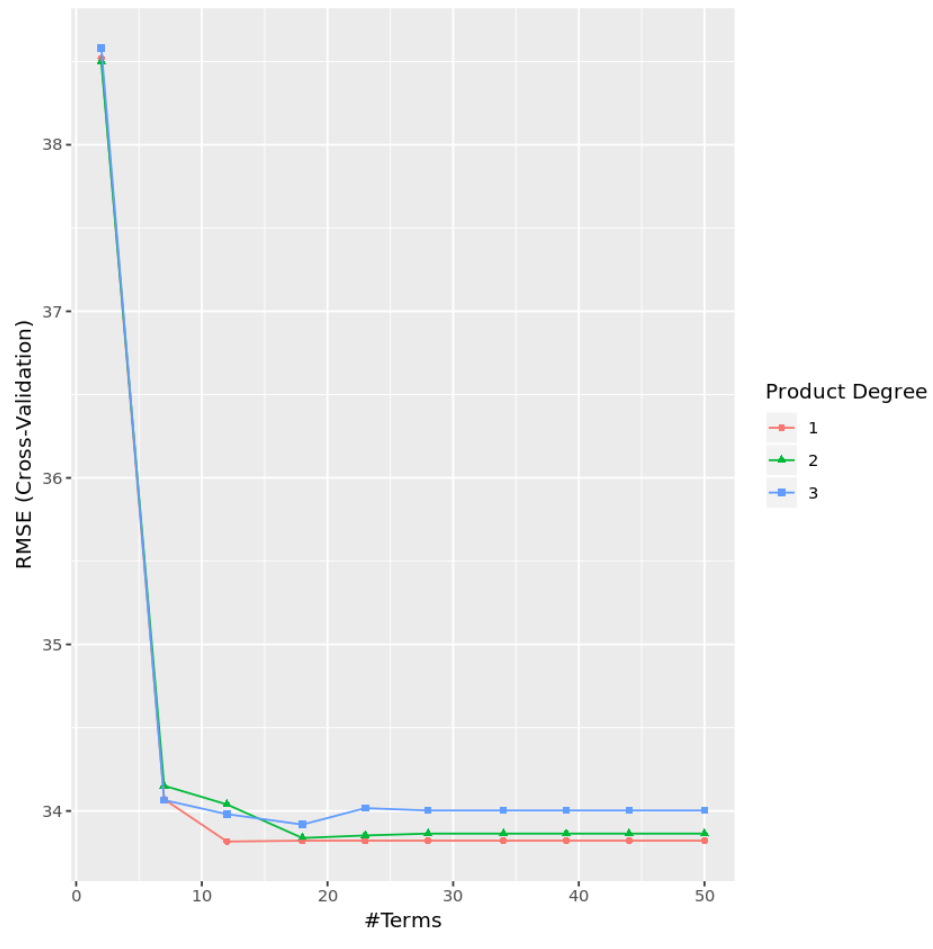
من الناحية العملية، يمكننا تكييف نموذج المريخ مع عدة أنواع أخرى من النماذج مثل:

• الانحدار الخطي المتعدد
• الانحدار متعدد الحدود
• ذروة الانحدار
• الانحدار لاسو
• انحدار المكونات الرئيسية
• المربعات الاقل جزئية

سنقوم بعد ذلك بمقارنة كل نموذج لتحديد النموذج الذي يؤدي إلى أقل خطأ في الاختبار واختيار هذا النموذج باعتباره النموذج الأمثل للاستخدام.

يمكن العثور على رمز R الكامل المستخدم في هذا المثال هنا .