تحليل المكون الرئيسي في r: مثال خطوة بخطوة

تحليل المكونات الرئيسية، والذي غالبًا ما يتم اختصاره PCA، هو تقنية تعلم آلي غير خاضعة للرقابة تسعى إلى العثور على المكونات الرئيسية – مجموعات خطية من المتنبئين الأصليين – التي تفسر جزءًا كبيرًا من الاختلاف في مجموعة البيانات.

الهدف من PCA هو شرح معظم التباين في مجموعة البيانات التي تحتوي على متغيرات أقل من مجموعة البيانات الأصلية.

بالنسبة لمجموعة بيانات معينة تحتوي على متغيرات p ، يمكننا فحص مخططات التشتت لكل مجموعة زوجية من المتغيرات، ولكن يمكن أن يصبح عدد مخططات التشتت كبيرًا بسرعة كبيرة.

بالنسبة للتنبؤات p ، توجد سحب نقطية p(p-1)/2.

لذلك، بالنسبة لمجموعة بيانات ذات تنبؤات p = 15، سيكون هناك 105 مخططات مبعثرة مختلفة!

لحسن الحظ، يوفر PCA طريقة للعثور على تمثيل منخفض الأبعاد لمجموعة البيانات التي تلتقط أكبر قدر ممكن من الاختلاف في البيانات.

إذا تمكنا من التقاط معظم التباين في بعدين فقط، فيمكننا إسقاط جميع الملاحظات من مجموعة البيانات الأصلية على مخطط تشتت بسيط.

الطريقة التي نجد بها المكونات الرئيسية هي كما يلي:

_{بالنظر إلى مجموعة بيانات ذات تنبؤات} p : _

• _{ض م = ΣΦ جم _}
• Z ₁ عبارة عن مجموعة خطية من المتنبئات التي تلتقط أكبر قدر ممكن من التباين.
• Z ₂ هي المجموعة الخطية التالية من المتنبئات التي تلتقط أكبر قدر من التباين بينما تكون متعامدة (أي غير مرتبطة) بـ Z ₁ .
• Z ₃ هي المجموعة الخطية التالية من المتنبئات التي تلتقط أكبر قدر من التباين بينما تكون متعامدة مع Z ₂ .
• وما إلى ذلك وهلم جرا.

من الناحية العملية، نستخدم الخطوات التالية لحساب المجموعات الخطية للمتنبئات الأصلية:

1. قم بقياس كل من المتغيرات للحصول على متوسط 0 وانحراف معياري 1.

2. احسب مصفوفة التغاير للمتغيرات المقاسة.

3. احسب القيم الذاتية لمصفوفة التغاير.

باستخدام الجبر الخطي، يمكننا أن نبين أن المتجه الذاتي الذي يتوافق مع أكبر قيمة ذاتية هو المكون الرئيسي الأول. وبعبارة أخرى، فإن هذا المزيج الخاص من المتنبئين يفسر التباين الأكبر في البيانات.

والمتجه الذاتي المقابل لثاني أكبر قيمة ذاتية هو المكون الرئيسي الثاني، وهكذا.

يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية تنفيذ هذه العملية في R.

الخطوة 1: تحميل البيانات

سنقوم أولاً بتحميل حزمة Tidyverse ، التي تحتوي على العديد من الوظائف المفيدة لتصور البيانات ومعالجتها:

 library (tidyverse)

في هذا المثال، سوف نستخدم مجموعة بيانات USArrests المضمنة في R، والتي تحتوي على عدد الاعتقالات لكل 100.000 مقيم في كل ولاية أمريكية في عام 1973 بتهمة القتل والاعتداء والاغتصاب .

ويشمل أيضًا النسبة المئوية لسكان كل ولاية الذين يعيشون في المناطق الحضرية، UrbanPop .

يوضح التعليمة البرمجية التالية كيفية تحميل وعرض الصفوف الأولى من مجموعة البيانات:

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

الخطوة 2: حساب المكونات الرئيسية

بعد تحميل البيانات، يمكننا استخدام وظيفة R المضمنة prcomp() لحساب المكونات الرئيسية لمجموعة البيانات.

تأكد من تحديد المقياس = TRUE بحيث يتم قياس كل من المتغيرات في مجموعة البيانات بحيث يكون متوسطها 0 وانحراف معياري قدره 1 قبل حساب المكونات الرئيسية.

لاحظ أيضًا أن المتجهات الذاتية في R تشير إلى الاتجاه السلبي افتراضيًا، لذلك سنضربها في -1 لعكس الإشارات.

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

يمكننا أن نرى أن المكون الرئيسي الأول (PC1) له قيم عالية للقتل والاعتداء والاغتصاب، مما يشير إلى أن هذا المكون الرئيسي يصف التباين الأكبر في هذه المتغيرات.

يمكننا أيضًا أن نرى أن المكون الرئيسي الثاني (PC2) له قيمة عالية لـ UrbanPop، مما يشير إلى أن هذا المكون الرئيسي يركز على سكان الحضر.

لاحظ أنه يتم تخزين درجات المكون الرئيسي لكل ولاية في results$x . سنقوم أيضًا بضرب هذه الدرجات في -1 لعكس العلامات:

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

الخطوة 3: تصور النتائج باستخدام مخطط ثنائي

بعد ذلك، يمكننا إنشاء مخطط ثنائي – مخطط يعرض كل الملاحظات الموجودة في مجموعة البيانات على مخطط مبعثر يستخدم المكونين الرئيسيين الأول والثاني كمحاور:

لاحظ أن المقياس = 0 يضمن تغيير حجم الأسهم الموجودة في المخطط لتمثيل عمليات التحميل.

 biplot(results, scale = 0 )

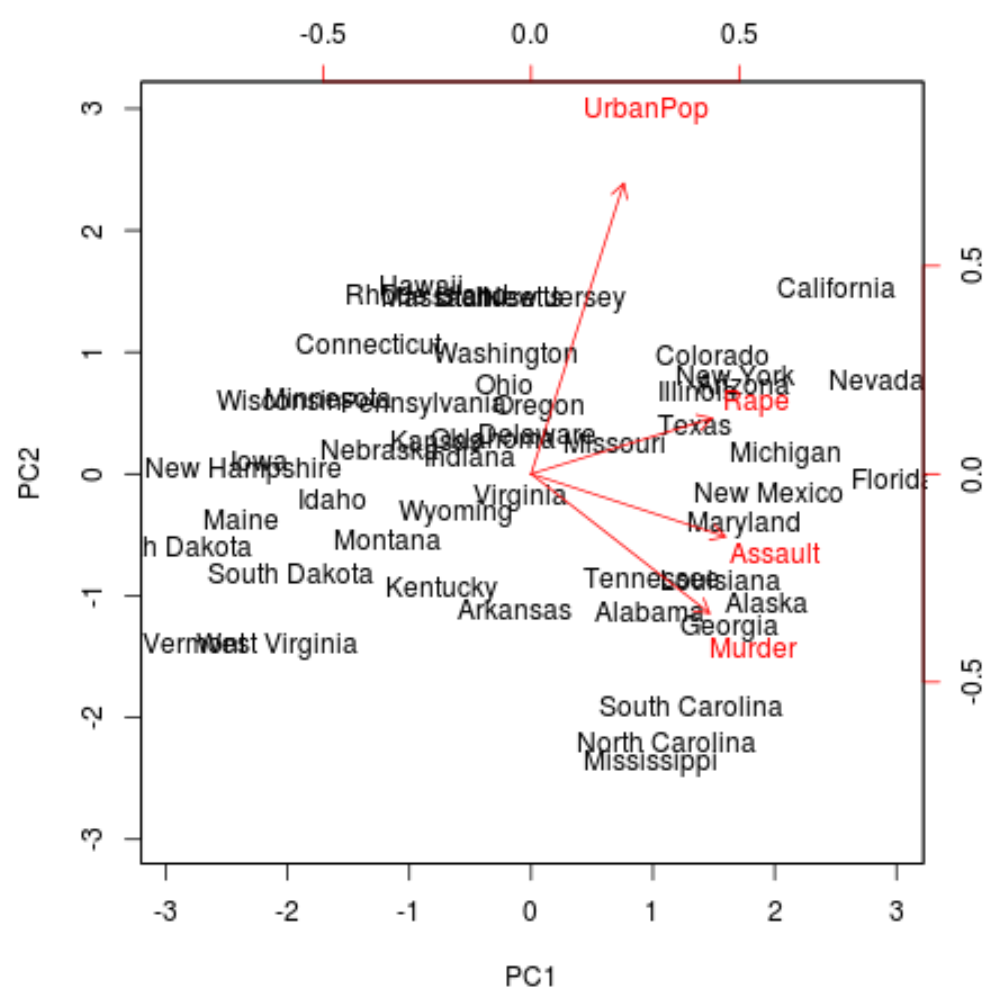
من المخطط يمكننا أن نرى كل ولاية من الولايات الخمسين ممثلة في مساحة بسيطة ثنائية الأبعاد.

الدول القريبة من بعضها البعض على الرسم البياني لديها أنماط بيانات مماثلة فيما يتعلق بالمتغيرات في مجموعة البيانات الأصلية.

يمكننا أيضًا أن نرى أن بعض الدول ترتبط بقوة بجرائم معينة أكثر من غيرها. على سبيل المثال، جورجيا هي الولاية الأقرب إلى متغير القتل في المؤامرة.

إذا نظرنا إلى الولايات التي لديها أعلى معدلات القتل في مجموعة البيانات الأصلية، يمكننا أن نرى أن جورجيا تتصدر القائمة بالفعل:

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

الخطوة 4: ابحث عن التباين الموضح لكل مكون رئيسي

يمكننا استخدام الكود التالي لحساب التباين الإجمالي في مجموعة البيانات الأصلية الموضحة بواسطة كل مكون رئيسي:

 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

ومن النتائج يمكننا ملاحظة ما يلي:

• يشرح المكون الرئيسي الأول 62% من إجمالي التباين في مجموعة البيانات.
• ويفسر المكون الرئيسي الثاني 24.7% من إجمالي التباين في مجموعة البيانات.
• ويفسر المكون الرئيسي الثالث 8.9% من إجمالي التباين في مجموعة البيانات.
• ويشرح المكون الرئيسي الرابع 4.3% من إجمالي التباين في مجموعة البيانات.

وبالتالي، فإن المكونين الرئيسيين الأولين يفسران غالبية التباين الإجمالي في البيانات.

وهذه علامة جيدة لأن المخطط الثنائي السابق أسقط كل الملاحظات من البيانات الأصلية على مخطط التشتت الذي أخذ في الاعتبار فقط المكونين الرئيسيين الأولين.

وبالتالي، فمن الصحيح فحص الأنماط الموجودة في المخطط الثنائي لتحديد الحالات المتشابهة مع بعضها البعض.

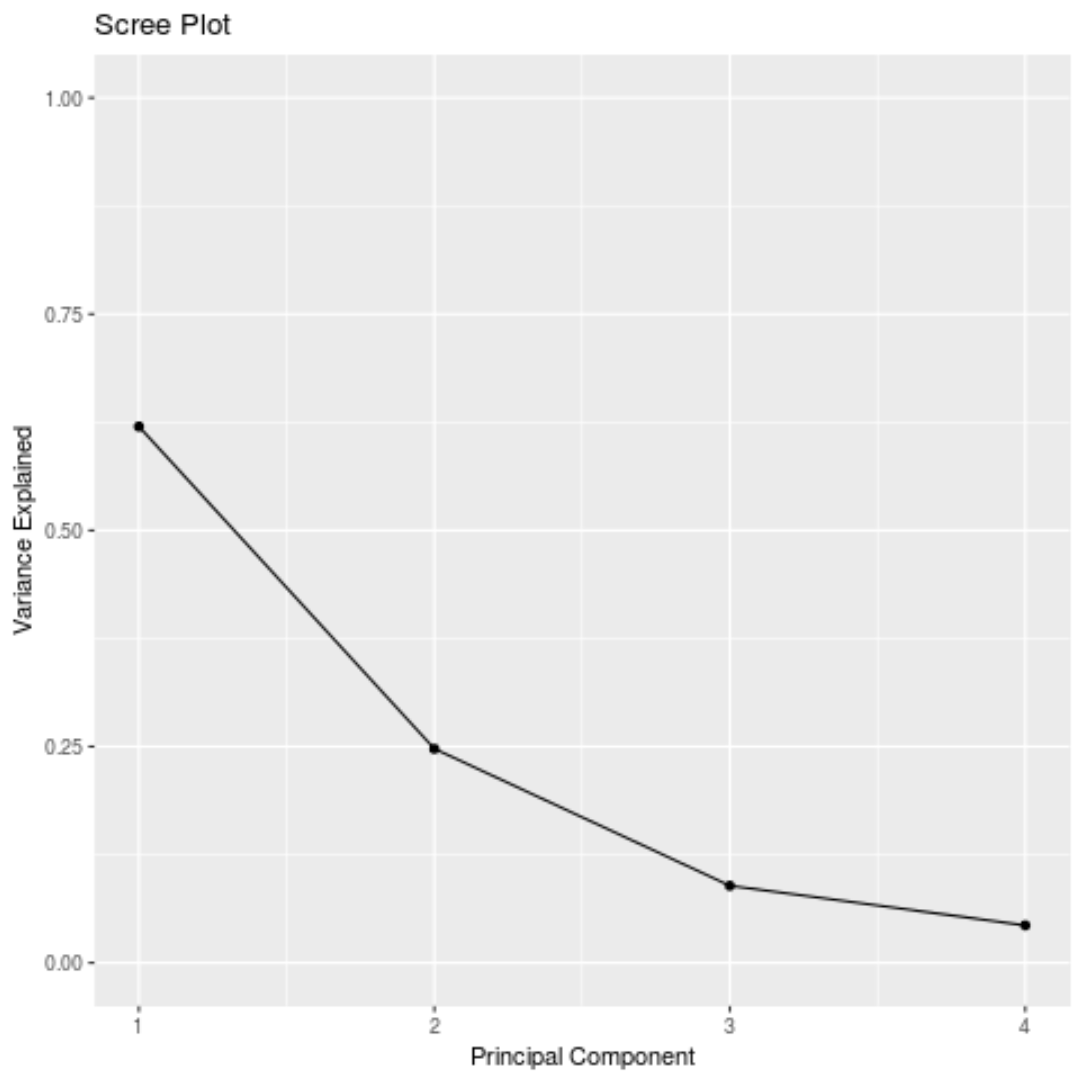
يمكننا أيضًا إنشاء مخطط حصوي – رسم بياني يعرض التباين الإجمالي الموضح بواسطة كل مكون رئيسي – لتصور نتائج PCA:

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

تحليل المكون الرئيسي في الممارسة العملية

من الناحية العملية، يتم استخدام PCA في أغلب الأحيان لسببين:

1. تحليل البيانات الاستكشافية – نستخدم PCA عندما نستكشف مجموعة بيانات لأول مرة ونريد أن نفهم الملاحظات الأكثر تشابهاً في البيانات مع بعضها البعض.

2. انحدار المكون الرئيسي – يمكننا أيضًا استخدام PCA لحساب المكونات الرئيسية والتي يمكن استخدامها بعد ذلك في انحدار المكون الرئيسي . غالبًا ما يستخدم هذا النوع من الانحدار عندما يكون هناك علاقة خطية متعددة بين المتنبئين في مجموعة البيانات.

يمكن العثور على رمز R الكامل المستخدم في هذا البرنامج التعليمي هنا .