كيفية إجراء اختبار scheffe في r

يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

إذا كانت القيمة الاحتمالية الإجمالية لجدول تحليل التباين (ANOVA) أقل من مستوى معين من الأهمية، فلدينا أدلة كافية لنقول أن إحدى وسائل المجموعة على الأقل تختلف عن الوسائل الأخرى.

ومع ذلك، هذا لا يخبرنا ما هي المجموعات التي تختلف عن بعضها البعض. وهذا يخبرنا ببساطة أنه ليست كل متوسطات المجموعة متساوية.

من أجل معرفة المجموعات التي تختلف عن بعضها البعض بالضبط، نحتاج إلى إجراء اختبار لاحق يمكنه التحكم في معدل الخطأ لكل عائلة .

أحد الاختبارات اللاحقة الأكثر استخدامًا هو اختبار شيفيه.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار Scheffe في R.

مثال: اختبار شيفيه في R

لنفترض أن المعلم يريد معرفة ما إذا كانت ثلاث تقنيات دراسة مختلفة تؤدي إلى درجات اختبار مختلفة بين الطلاب أم لا. ولاختبار ذلك، قامت بتعيين 10 طلاب بشكل عشوائي لاستخدام كل أسلوب من أساليب الدراسة وتسجيل نتائج امتحاناتهم.

يمكننا استخدام الخطوات التالية في R لتناسب ANOVA أحادي الاتجاه لاختبار الاختلافات في متوسط درجات الاختبار بين المجموعات الثلاث واستخدام اختبار Scheffe لتحديد المجموعات المختلفة بالضبط.

الخطوة 1: إنشاء مجموعة البيانات.

يوضح الكود التالي كيفية إنشاء مجموعة بيانات تحتوي على نتائج الامتحانات لجميع الطلاب الثلاثين:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

الخطوة الثانية: عرض نتائج الامتحانات لكل مجموعة.

يوضح الكود التالي كيفية إنتاج boxplots لتصور توزيع نتائج الاختبار لكل مجموعة:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

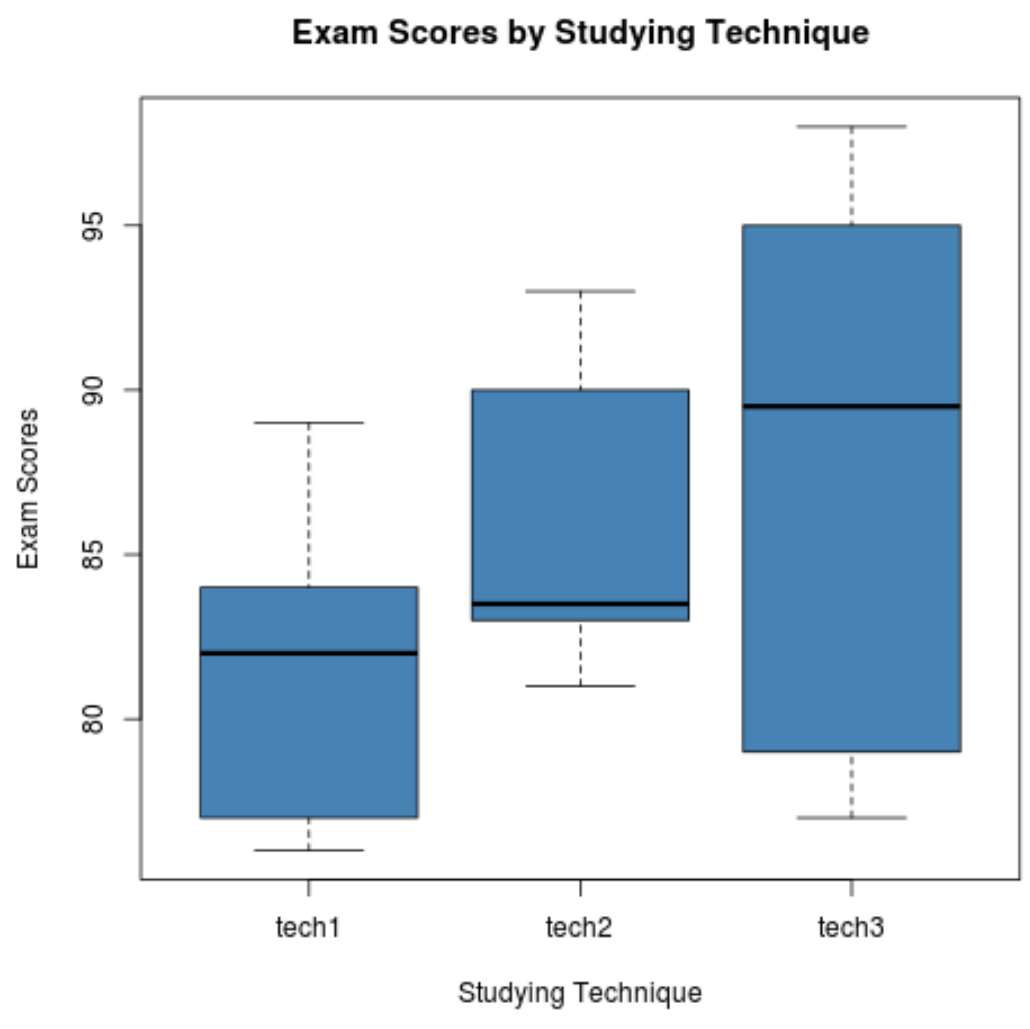
الخطوة 3: إجراء تحليل التباين (ANOVA) في اتجاه واحد.

يوضح الكود التالي كيفية إجراء تحليل التباين (ANOVA) أحادي الاتجاه لاختبار الاختلافات بين متوسط درجات الاختبار في كل مجموعة:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

وبما أن القيمة الاحتمالية الإجمالية ( 0.0476 ) أقل من 0.05، فهذا يشير إلى أن كل مجموعة ليس لديها نفس متوسط درجات الاختبار.

بعد ذلك، سنقوم بإجراء اختبار شيفيه لتحديد المجموعات المختلفة.

الخطوة 4: إجراء اختبار شيفيه.

لإجراء اختبار Scheffe، سوف نستخدم الدالة ScheffeTest() من حزمة DescTools .

يوضح الكود التالي كيفية استخدام هذه الوظيفة لمثالنا:

 #load DescTools package
library(DescTools)

#perform Scheffe's test
ScheffeTest(model)

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$technical
            diff lwr.ci upr.ci pval    
tech2-tech1 4.2 -2.24527202 10.645272 0.2582    
tech3-tech1 6.4 -0.04527202 12.845272 0.0519 .  
tech3-tech2 2.2 -4.24527202 8.645272 0.6803    

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

وطريقة تفسير النتيجة هي كما يلي:

• متوسط الفرق في نتائج الامتحان بين التقنية 2 والتقنية 1 هو 4.2 . القيمة p المقابلة لفرق المتوسط هي 0.2582 .
• متوسط الفرق في نتائج الامتحان بين التقنية 3 والتقنية 1 هو 6.4 . القيمة p المقابلة لفرق المتوسط هي 0.0519 .
• متوسط الفرق في نتائج الامتحان بين التقنية 3 والتقنية 2 هو 2.2 . القيمة p المقابلة لفرق المتوسط هي 0.6803 .

اعتمادًا على مستوى الأهمية الذي نقرر استخدامه، فإن المجموعتين الوحيدتين اللتين تبدوان مختلفتين بشكل ملحوظ إحصائيًا هما التقنية 3 والتقنية 1.

مصادر إضافية

كيفية إجراء ANOVA أحادي الاتجاه في R
كيفية إجراء اختبار توكي في R
كيفية إجراء تصحيح Bonferroni في R